Evolving
Fractal Drawings
Jon Bird, PhD
Centre for
Computational Neuroscience and Robotics, University of Sussex, U.K.
Dustin Stokes, PhD
Centre for
Research in Cognitive Science, University of Sussex, U.K.
Abstrac
We are using an evolutionary robotics approach to generate minimal
models of creativity. Our preliminary simulation results demonstrate that this
methodology can produce robots that mark their environments and interact with
the lines that they have made. These simulated robots possess a ‘no strings
attached’ form of agency and some of their behaviour can be described as novel
relative to their individual behavioural histories and to the behaviours of
other members of the evolving population.
Arguably, they thus satisfy two conditions necessary for creativity:
agency and novelty. Open questions
remain: Are the robots’ behaviours
creative? Will they become creative as
we incrementally increase the complexity of the robot controllers? Can their mark making be classified as
drawing?
A number of common criticisms of the project fall under the broad
category of value. In the
preliminary model the robots neither evaluate the process nor the product of
mark making. The robots can only detect
the presence of a mark in a 2mm x 2mm region underneath them. How could an
agent, from such a ‘myopic’ viewpoint, have any sense of the global pattern of
the marks made across a large arena? And
how could such agents have any sense of when to stop? Finally, the present results fall short of our artistic goal of
producing a gallery exhibit, since currently the products of these robots are
unlikely to engage audiences (without considerable knowledge of the methodology
involved).
Here we outline a fractal framework that addresses each of these
concerns: our robots will be endowed with a ‘fractal detector’; and they will
acquire fitness for making marks with a self-similar structure. The robots will be able to interact with
their products in a way that involves a kind of judgment of the product as it
is being produced. Although their
viewpoint will still be limited to a local region, the robots will be able to
generate a coherent self-similar pattern across the arena without requiring a
global perspective mechanism, such as a bird’s-eye view camera or topographic
memory. The framework will also provide
a natural finishing criterion: once a self-similar pattern covers the arena the
robots will no longer make marks. Finally,
fractal images do engage people. And
knowledge that these agents have a ‘fractal preference’ should enhance that
engagement, since audiences will be able to watch the development of a global
self-similar pattern through the simultaneous mark making of a group of
robots.
Minimal Robotic Creativity
Philosophical analysis of creativity does not come easy. Evolving artificial agency comes no
easier. We are doing both at once. Our
research team thus comprises artificial life researchers, philosophers,
cognitive scientists, and artists, all of us motivated to evolve some kind of
creative behaviour. We here outline a
theoretical framework for extending our evolutionary robotics (ER) approach to
generating models of minimal creativity. The focus is on the role of evaluation
in creativity and how that role might be accommodated in our robotic models
using a fractal framework[1].
Philosophical
analysis
Our assumptions about creativity are minimal. We start with only two conditions, each of them necessary but
non-sufficient, for creativity. A
creative behaviour must result from agency.
Agency requires autonomy. Our
sense of the term does not require, as the philosophical sense does,
intentionality, deliberation, or cognition.
It simply requires behaviour that is not imposed by an external agent or
programmer. A remote controlled robot
would thus not qualify, while many of the systems that populate evolutionary
robotics would. We sometimes refer to
this as ‘no strings attached agency.’
Intuitions also tell us that novelty is a condition for creativity:
creative artefacts or processes are novel ones. Here too we err towards barely minimal assumptions. Following Boden [3], we distinguish absolute
and relative forms of novelty. As Boden
argues, relative novelty is sometimes as theoretically interesting as absolute
novelty. For example, one may have a
novel thought which, although others have had it before, is novel relative to
one’s own mind. We broaden the
latter—which is what Boden calls ‘psychological’ novelty—to include
non-cognitive behaviours. This is done
in two ways. A behaviour of some agent R may be novel relative to the behavioural history
of R. Or a behaviour of some
agent R may be novel relative to a population of which R is a
member. Call the first
‘individual-relative novelty’; call the second ‘population-relative novelty.’
The choice for conceptualizing agency and novelty so thinly is motivated
both by our particular research goals and a general methodological assumption
we share with much of cognitive science. Our interest is to see what lessons
can be learned about creativity and cognition though the use of synthetic,
bottom-up modelling techniques. We may, after all, be working with overly thin
notions, but the working supposition that weaker instances of agency and
novelty may be near what’s necessary for creative behaviour enables
fruitful experimentation and hypothesis generation. This is often how cognitive scientists begin, that is, by asking
what might some minimal conditions be for some phenomenon, and what can we
learn from attempting to satisfy just those conditions?
The agency and novelty conditions give us two necessary conditions for
creativity. The weakness of this
definition is easy to see. I can right
now place my head in the oven and utter ‘We need milk, butter, and bread.’ This is novel behaviour for me, and indeed
behaviour that depends upon my autonomy.
But would anyone count it creative?
Novelty and agency, even of a very rich, cognitive sort, are thus not
enough for creativity. We recognize
that, and the point of this paper and the project stage it outlines is to
determine what is enough, even minimally. Nonetheless, we have to this point been proceeding with this
incomplete definition in hand: creativity requires agency and novelty. So if we are going to build creative
systems, we at least have to build systems that possess these two properties. This, as it turns out, is hard enough as a
start.
Evolutionary robotics
methodology
We use an evolutionary robotics
methodology for two main reasons. First, it is an established technique for
developing situated robot controllers (and to a limited extent their
morphology). Second, ER can potentially generate models of minimal creativity
that overcome the limitations of our understanding of creativity. This is
possible because we aim to minimise the constraints that we place on the
controller architecture by artificially evolving artificial neural network
(ANN) controllers from low-level primitives (processing units and the
connections between them). The evolutionary
process is also free to exploit any constraints that arise from the interaction
of the robot and the environment that may not be apparent to an
experimenter. ER can therefore generate
controller architectures to solve problems that are not well-defined.
Initially, we have carried out our experiments in simulation using a
model of a Khepera robot based on empirical measurements, a standard ER
platform (Figure 1a). This approach has advantages over doing evolution on
physical robots: it is far quicker; and it avoids damage to the robots during
early evolutionary stages when the controllers
often crash into the arena walls. Bill Bigge, a researcher on the DrawBots
project, is developing a custom robot for testing our controllers in the real
world (Figure 1b).


Figure 1: a) a
Khepera robot modelled in our initial simulation experiments;
b) prototype
DrawBot for testing controllers in the real world.
In simulation, each robot controller consists of seven sensors (six
frontal IR sensors and one line detector positioned under the robot) and six
motor neurons (a pair of motor neurons controlling the left wheel, right wheel
and the position of the pen - up or down). At each time step in the simulation,
the most strongly activated neuron of each pair controls its associated
actuator. Each of the seven sensors connects to each of the six motor neurons. A
genetic algorithm is used to determine the strength of each of these
connections and the bias of each of the motor neurons.
An initial population of 100
robots controllers (phenotypes) is encoded as a string of 0s and 1s (genotypes). Every generation each genotype
is decoded and the performance of the robot controller is tested and assigned a
fitness value. A new generation of genotypes is then generated by randomly
selecting genotypes, with a bias towards fitter ones, and mutating them
(flipping 0s to 1s or 1s to 0s with a probability of 0.01 per gene). Our
experiments were carried out for 600 generations.
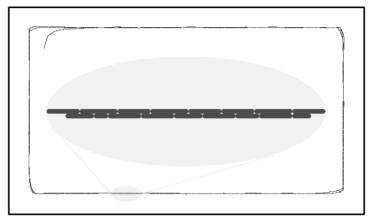
Figure 2: a high fitness individual from an initial experiment – it does an
initial loop of the arena with its pen down and on the second loop makes line
segments parallel to the line it initially made.
We aim for
fitness functions that minimise our influence on the resulting robot behaviour.
We do not specify the types of marks that a robot should make, rather, we
reward controllers that correlate the changes in state of their line detector
and pen position. For example, if a line is detected and the robot’s pen is
then raised or lowered within a short time window, the robot accumulates
fitness. This fitness function resulted in robots that followed the walls and
made marks around the edge of the arena (Figure 2). When the fitness function
also rewards robots for making marks over the whole area of the arena then
different behaviours evolve (Figure 3) and robots turn away from the walls at angles
and mark the central parts of the arena as well. In all our experiments
crashing into walls is implicitly penalised by stopping the evaluation and
thereby giving the robots less time to accumulate fitness. It is important to
note that although we, via the fitness function, evaluate the mark making
behaviour of the robots, the robots themselves do not assess the marks that
they have made.
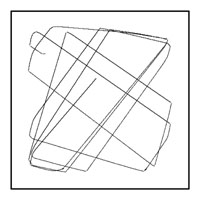
Figure 3: when the fitness function rewards making marks
over the whole arena, the robots no longer follow the walls but turn away from
them at angles and mark more central regions.
On What’s Missing: Value
As we stated at the outset, our working assumptions about creativity are
minimal; we do not purport to have offered a complete analysis of creativity
nor to have evolved any richly creative behaviour. “Fair enough”, one might respond, “but can you evolve rich
creativity? Creative behaviours involve
evaluation, and creative artefacts, for example, artworks, are things we
value. So if your research does not yet
address these facts, can it ever address them?” We give two responses to this general
worry. One, we allow that some kind of
value condition may be what’s needed for a complete analysis of
creativity. That is, perhaps value plus
agency and novelty will get you creativity.
We are willing to take this as a plausible suggestion, without
committing to the claim that the conjunction of these three properties is
sufficient. Rather, we merely accept
that value is a good general area to mine in the search for richer models of
creativity. Our second response is more
straightforward. We believe we can
address the concerns about value by extending our robotics framework. We now
distinguish four such concerns.
1. The non-evaluative process worry
If creativity is a process, that process must involve some kind of
evaluation: the agent needs to make judgments about the behaviours it is
performing, and those judgments must in turn play some important role in the
dynamic process of creation. There are
many ways of developing this thought further, but the basic idea is just that
agents must make choices of some sort in acting creatively, preferring one
option over another, this action over that one, and so on. Without this evaluative feature of the
process, we seem to have purely reactive behaviour. Our robots seem to suffer from this very problem. There is nothing like evaluation in their
mark-making behaviour. They simply
react in a way that at most depends upon sensory motor morphology, the arena
boundaries, previous engagements with that environment, and (if the agent is of
a later generation) the performance of agents in previous generations. Nowhere in that causal chain is there
anything that looks like judgment or evaluation. The robot’s mark making processes are thus non-evaluative.
2. The myopic
worry
This worry is intimately tied with the one just canvassed. In fact, it is partly explanatory of the
non-evaluative problem. As a simple
feature of their physical structure, our robots can only “see” marks that are
underneath their 2mm x 2mm line detector.
Their viewpoint is thus myopic. This is problematic if we think of
artistic creation (or, analogously, of creativity in non-artistic realms). A painter, for example, will often focus on
a small component of her painting, but will return to the larger work of which
that component is just one part. Without
such capacity, we would never get pictorial representation. And the point generalizes to
non-representational paintings (and artworks generally): Rothko, Mondrian,
Pollock and the like took a step back from their work to “see the picture” even
if it wasn’t picturing anything. This
is part of the creative process and, what’s more, it is essential to the
artist’s evaluation of her own work.
Without a more global perspective of the work and how its parts
constitute the whole, the artist has little to evaluate, scrutinize, and
change. Our robots are stuck with a
local perspective of the marking surface, and no memory to conjoin each of
these perspectives for something more global.
This partly explains why the process is non-evaluative. It is blocked from being evaluative, since
if you don’t see the whole picture, you certainly cannot evaluate it.
3. The never ending worry
If the processes of our agents have an end point, it is at best
arbitrary, unrelated to whatever marks have been made on the marking
surface. This is at tension with how we
think about artworks. Artworks,
excepting a very small number of cases, are spatially and/or temporally bound. They have distinct stopping points. We can see that a portrait or sculpture or
film is finished. We can hear when a
musical performance or recording concludes.
And the artists in question make this decision: they decide when the
work is done and where its spatial and temporal boundaries lie. Our robots have no such stopping
mechanism. Or better, whatever stops
them—namely, either they crash into the arena boundaries, or the trial comes to
an end when they complete a specified number of time steps—it has nothing to do
with there being some product which that agent decides is finished. This is a problem. We are never going to get gallery displayable images out of these
systems if there is no mechanism which encourages a non-trivial stopping point.
4. The aesthetic merit worry, or the “You say a robot
did that?” worry
In addition to
our motivations to learn about creative processes, members of our research team
would ultimately like some results that can be exhibited. More precisely, we would like some results
worthy of aesthetic appreciation, where that appreciation does not stand or
fall with knowledge of the robotic systems that produced those results. At present, our results would at best
warrant appreciation of the latter sort.
That is, perhaps if one were informed about the artificial life and
robotics techniques responsible for evolving the mark structures, one might
attribute some aesthetic merit to those patterns. Perhaps. But one is very
unlikely, if lacking such knowledge, to look at Figures 2 and 3 and say “how
interesting”, “lovely”, “beautiful” and so on.
The patterns themselves are, quite frankly, not particularly
aesthetically interesting.
One might
respond, of course, by invoking the same feature of much of modern art. Contemporary art museums are full of
conceptual works, found artefacts, and performances, the appreciation of which
requires knowledge of art history and theory.
So if our images require contextual knowledge, that puts them in no
worse a position than lots of artworks.
We acknowledge this (and will certainly keep it in our back pocket
should such a defence be needed), but we also acknowledge that much of art is
not of this sort. One needn’t know
much, if anything, to “just see” the beauty in a Rodin sculpture or a Vermeer
painting. In fact refusing to see the
merit in such works would likely indicate that you were either a tasteless fool
or an elitist attempting some kind of snobbish irony. Some artworks, on their own, just are aesthetically
valuable. And although our hopes are
humble ones, we would like some mark patterns whose formal properties alone
warrant aesthetic appreciation. So far
we are a long way from reaching this goal.
Towards a Richer Robotic
Creativity: A Fractal Framework
The above are
all significant worries. They identify
a general evaluative constraint on theories of creativity that many seem to
endorse. And they reveal how the
current state of our research falls short of that mark. These challenges are not, however,
insurmountable. We think they can be
addressed, and without compromise of our overall theoretical and methodological
preference: minimal assumptions and bottom-up modelling.
One solution,
in a word, is fractals. Fractals,
understood broadly, are patterns which display self-similarity at different
magnifications [4]. We intend to use
them in the following ways. Endow the
agents with a ‘fractal detector.’ Endow
the agents further with a ‘fractal preference’, such that they will acquire
fitness for making fractal patterns on the arena surface. In the next section we outline how we plan
to evolve robots that make and evaluate fractal patterns. We then discuss how
this approach is sufficient to address each of the four value worries discussed
above.
How can a robot measure
fractal dimension?
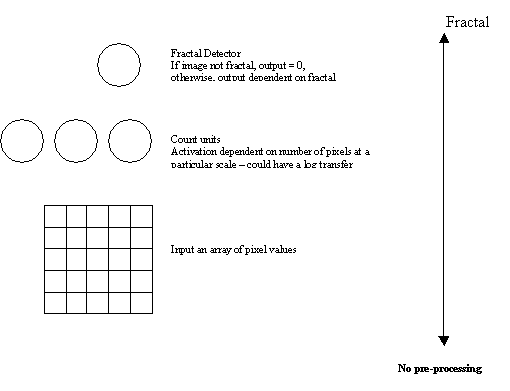
Figure 4: different degrees of pre-processing of a camera
image before an ANN measures its fractal dimension.
There are
various options for endowing the robot with a fractal detection capacity. The
simplest and most widely used approach for measuring the fractal dimension of a
structure is the box counting method. A binary image of the structure is
divided into a grid of uniform cell size. The number of cells or boxes in the
grid which contain one or more black pixels (assuming the image is black) are
counted. The size of the grid cells is varied, generally ranging from larger
than 1 pixel to less than the size of the image. For each cell size, the number
of cells containing parts of the image is counted. The log of the box size is
then plotted against the log of the number of boxes containing part of the
image. If an image is fractal then the data points fall on a straight line and
the slope of this line gives the fractal dimension. There are other approaches
to measuring fractal dimension, such as decomposing the image into its power
spectrum. However, because of its conceptual simplicity, our initial approach
is to deconstruct the box counting algorithm and consider which steps we will
pre-process and which parts we will leave open to the evolutionary algorithm to
configure (Figure 4).
The robot will
be fitted with a camera and one option is to do no pre-processing on the image
and supply the controller with an array of grey level values. It is an
extremely challenging task to artificially evolve an ANN to use these raw pixel
values to identify fractals. The ‘no
pre-processing’ option appears untenable given the time scale of our project.
At the opposite extreme, we could use a box counting algorithm to process the
camera image and provide the controller with a hardwired ‘fractal detector’
unit whose activation is 0 if the image is non-fractal or a positive value
(< 1.0) that is proportional to the fractal dimension of the image. As we
have done all of the processing up front, this approach is open to the
criticism that the robots are still not evaluating their mark making.
We are
therefore initially implementing a ‘count unit’ approach to provide information
about structure in the camera image at different scales. Each unit is
associated with a different box size and their activation is dependent on the
number of boxes which contain marks. We will explore the effect of using
different transfer functions for these units. For example, we could use a
logarithmic function, analogous to the box counting algorithm and leave the ANN
to compare the activation of the different count units to determine whether the
mark structure is fractal.
Steps towards evolving fractal drawing
We want to
leave the evolutionary algorithm some freedom in how it uses the camera
activation and configures the ANN to detect fractals. First, the less
pre-processing we do on the image, the stronger our claims that the robots are
determining, to some extent, the evaluation criteria. Second, dynamically
estimating the fractal dimension of a changing structure is not a well-defined
problem and we are currently unclear about how we should extend our ANN
primitives to enable the robot to solve this problem. Unlike most applications
of fractal dimension analysis, the robot will be making an estimation of a
dynamic structure: it will be both moving across the arena floor and have the
ability to change the mark structure with its
pen. This is a non-trivial task that is at least approaching the order of complexity
of some of the most challenging behavioural tasks that have been accomplished
using an ER methodology [6]. One open question concerns the extent to which the
controllers will require some form of memory and whether this could be
implemented with ANN primitives such as recurrent connections. ER is a
discovery methodology that can potentially evolve controllers that can solve
this problem.
We plan to
carry out a series of experiments of increasing behavioural complexity.
Initially we will focus on getting a robot to discriminate between fractal and
non-fractal structures. The camera will be pointed forwards so that it can view
patterns on the arena walls and robots will gain fitness for staying in a
region in front of a wall area that has a fractal pattern; the other walls will
have random patterns which have the same pixel density as the fractal pattern[2].
The next step will be to determine whether robots can discriminate between wall
patterns with different fractal dimensions. These two experiments will be
important to clarify the neural network primitives that are required and to test the sufficiency of the ‘count units’ approach.
Assuming we
accomplish the above, the next step is to get robots to draw fractal patterns.
In our initial experiments the fitness function will reward the area of arena
covered with self-similar mark structures. It is an open question whether the
robots have sufficient degrees of freedom to generate fractal marks. It may be
that we have to add another degree of freedom to the pen and enable it to move
from side to side as well as up and down. Another option that we might have to
explore is building reactive drawing behaviours into the ANNs. There are also a
number of issues that have to be explored concerning the camera: where should
it point – in front of the pen?; what size image should we use?; and over how
many scales can we expect the robots to generate self-similar marks?
Conclusion
Even though
there are many challenges to be solved before we evolve robots that make
self-similar patterns, we are keen to pursue the fractal framework we have
outlined as it addresses all four value worries that we described earlier in
the paper.
Addressing worries 1 and 2: Fractal evaluation
The behaviour
of our artificial agents lacks an evaluative component for a rather simple
reason: our agents aren’t looking for particular mark structures. They
simply respond to any marks under their line detector. And given the small size of this sensor (2mm
x 2mm) they also have a myopic perspective.
Consider the
myopic worry first, since addressing it will contribute to a solution to the
non-evaluative process worry. Obvious solutions to the worry might involve
incorporating a bird’s eye view camera in the overall system, or endowing the
ANN with a topographic memory of some sort.
These may well be viable options.
But they may also be unnecessary if fractal patterns being detected and
constructed. A self-similar pattern can
be completed in the agent’s local surface area. When a fit agent moves across the surface, it will continue to
implement this pattern, making marks on parts of the surface which are not
self-similar. These adjustments
contribute to the overall pattern of self-similarity, but without the need for
any topographic memory or global view of the surface. In a sense then, by looking for a fractal pattern in any given
local region, the agent is working on the bigger picture without having to
actually look at the bigger picture and its myopia is thus rendered
harmless with respect the worry at hand.
How does all
of this help with evaluation? The
proposed framework neutralizes the myopia of our earlier agents not by giving
them a global viewpoint, but by taking advantage of the nature of fractal
patterns. If a region of marked surface
isn’t self-similar, then a fit agent will detect this and add marks to make it self-similar. The agent thus has
something to look for and a preference for making things that look a certain
way. This capacity is admittedly not a
sophisticated aesthetic or artistic one.
But it is an evaluation technique, which results in the agent making
choices: it will prefer some marks over others, and will change some and leave
others. Moreover, fractals are a broad
enough pattern category that the agents have considerable freedom in the marks
they can make.
Addressing worry 3: Done!
The never ending worry, recall, was that the mark making behaviour of
the agents has no non-trivial stopping point: if the agent does stop, it has
nothing to do with the completion of some pattern. The fractal framework makes quick work of this worry: at some
point, the arena surface will be with a self-similar pattern and the robot will
no longer add any more marks.
Addressing worry
4: The aesthetic appeal of fractals
People
generally like fractals, or at least that is what experimental studies show us
[5]. There is a lot to say here, but
here are just a few intuitive reasons to think that fractal patterns created by
our agents would (self-sufficiently) be aesthetically interesting. Fractal patterns are detectable. That is, they are identifiable patterns, and
so part of the engagement when viewing them is finding the self-similarity at
different magnifications. Second, the
range of self-similar patterns that the robots can produce is potentially very
broad and the resulting marks may surprise us. An element of surprise is an
aesthetic merit, and thus a potential benefit of the fractal framework.
To be clear,
none of this is intended to show that our agents are or would be producing
artworks. What makes something an
artwork is an extremely deep and rich issue, and one that likely depends upon a
number of factors: context, theory, and artistic intention for starters. Our robots might be behaving in
minimally creative ways and making marks in aesthetically interesting ways, but
we remain agnostic on the question of whether they are making art. However, we
are confident that the fractal framework that we have outlined in this paper is
a promising approach for investigating value issues with minimal models of
creativity.
5.1
Acknowledgements
The Computational Intelligence,
Creativity and Cognition project is funded by the AHRC and led by Paul
Brown in collaboration with Phil Husbands, Margaret Boden and Charlie Gere.
References
[1] J. Bird,
D. Stokes, P. Husbands, P. Brown and B. Bigge, Towards Autonomous Artworks. Leonardo
Electronic Almanac, 2007 (in press).
[2] J. Bird and D. Stokes, Evolving Minimally Creative
Robots. In S. Colton and A. Pease (Eds.) Proceedings of The Third Joint
Workshop on Computational Creativity (ECAI '06), 1 - 5, 2006.
[3] M. A.
Boden, The Creative Mind. Routledge, 2004.
[4] B. B. Mandelbrot, The
Fractal Geometry of Nature, W.H. Freeman and Company, 2007.
[5] R. P. Taylor, Fractal
expressionism - where art meets science. In J. Casti and A. Karlqvist (Eds.) Art and Complexity, Elsevier
Press, 2003.
[6]
D.Floreano, P. Husbands, S. Nolfi, Evolutionary Robotics. In B.
Sicilianoand O. Khatib (Eds.) Springer
Handbook of Robotics, Chapter 63, Springer, 2007 (in press).
[7]
T.M.C.
Smith, P. Husbands, A. Philippides and M. O'Shea, Neuronal plasticity and
temporal adaptivity: GasNet robot control networks. Adaptive Behavior,
10(3/4), 161-184, 2002.