ArpEgg: a Rewriting Grammar for Complex Arpeggios

Kevin McGuire

Ottawa, Canada

e-mail: kevin@mcguire.name

Abstract

Arpeggiators are hardware or software devices for producing a series of musical notes from an input chord. They are used extensively in many forms of music, in particular electronic dance music. As such, they are probably one of the most prevalent forms of generative art in our popular culture.

Yet the vast majority of arpeggiators encode a relatively small and simple set of algorithms for note generation, and thus have fairly predictable results. For the artist, this limited palette of algorithms can be creatively constraining. In an attempt to solve this, most arpeggiators have a “random” setting. While this produces more complex results, the experience for the musician is extremely hit-and-miss, forgoing any form of control over the process itself. The artist must rely on luck that a random sequence will be suitable. Neither extreme is very satisfactory. Surely there must exist points in between, where the musician has both expressive power and rich results?

We introduce ArpEgg, a software arpeggio authoring system based on a modified LSystem grammar. ArpEgg uses small sets of rewriting rules to transform input chords into complex, evolving streams of notes. We show how typical arpeggiation patterns can be expressed in ArpEgg, and how simple ArpEgg grammars can generate complex patterns. ArpEgg represents one attempt at exploring this middle ground of complexity with control.

1. Introduction

An arpeggio is “a chord where the notes are played or sung in succession rather than simultaneously” [14]. An arpeggiator is “a tool/feature available in some hardware synthesizers and also in software form, which allows the user to automatically play alternating notes or chords based on input” [15]. Arpeggios are popularly found in many forms of electronic music, in particular Trance and Techno. Most software music sequencers (e.g. Cubase[3], Sonar[13], Ableton Live[1]) include some form of arpeggiator, as do many software and hardware synthesizers (e.g. Albino [2]).

Arpeggiators generate a pattern of notes, based on the input chord, according to some algorithm. The simplest of these strategies, “Up”, starts with the root note of the chord, followed by the next higher chord note, followed by the next, etc. This pattern can be repeated for some number of octaves. Once the octaves are exhausted, it starts from the bottom again. Its inverse algorithm, “Down”, starts at the highest note in the chord and progresses downwards in successive chord notes. These can be combined into “Up&Down”, proceeding upwards through the chord, and on reaching the top, descending to the root note, producing a mirror image of the ascending notes.

Most arpeggiators only offer a fairly small set of patterns. For example, Sonar’s arpeggiator only contains the four just listed, and even the relatively sophisticated Ableton Live 5.0 has but seven distinct patterns (plus their inverses) and three variations on a “random” pattern.

Excluding the random ones, these patterns produce recognizably simple and repetitive results. Musical variety is instead created by pre or post processing techniques like increasing the octave range, repeating the pattern offset by semitones, modifying the velocity and duration of notes, etc. Furthermore, the list of patterns is fixed.

To address this, most arpeggiators provide a “random” pattern. The problem though with a “random” pattern is that, by definition, the results are unpredictable; the musician has no ability to predict or control the outcome. While serendipity is a valuable creative trigger, the random function of an arpeggiator reduces the expressiveness of the software as instrument.

Furthermore, a random pattern is unlikely to be very listenable. Most forms of music have intrinsic structure that we may innately recognize at some level, analogous to innateness of language [6]. Yet a random process has no (apparent) structure. This lack of structure is therefore unlikely to produce something that we would commonly describe as musical, much in the same way that banging randomly on a piano is unlikely to result in anything particularly pleasing. Structure is important. Thus the artist has a very limited palette of arpeggio algorithms to choose from, which are either too simple or too complex (random).

We turn to generative approaches. These have been shown to exhibit complex structure with variety, using simple deterministic rules in a controllable manner [8].

2. The Middle Ground of Complexity

Lets us consider for a moment the notion of information content. The Kolmogorov complexity of an object is a measure of its algorithmic complexity [5]. Put simply, it is the length of the smallest Turing Machine (i.e. program) capable of producing the object. Although we will not detail a Kolmogorov analysis of arpeggio algorithms, it is a useful conceptual framework to think about relative complexity.

With that in mind, the arpeggio algorithms discussed thus far are extremely simple: it would be straightforward to come up with very small Turning Machines to generate all but the “random” pattern. This is evidenced by the fact that we could list out the steps for producing “Up”, “Down”, and “Up&Down” in such simple words. At the other extreme is a purely random string. What of the vast algorithmic space in between (Figure 1)?

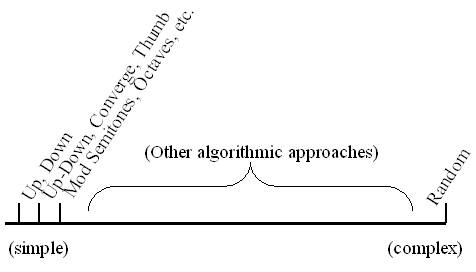
Figure 1: Opportunity for Algorithmic Approaches

What we require is a generative approach that will encode a wider range of structures, from simple to complex. But this approach must also be expressive in the sense that an artist can develop and execute their vision of the music.

The space in between is thus ripe for generative approaches.

3. Previous Algorithmic Approaches

There have been a number of approaches to the subject of grammars for music. Lerdahl [6] takes a generative theoretical approach with focus on the inherent relationship of generative structure to well known pieces of Western tonal music. Holztman [4] is an early attempt at generative grammars. Psenicka [11] focused on rewriting rules with a wide range of interpretation of the symbols, at many levels of expansion. It permits an interactive role for the musician to direct the process and craft the outcome while still working within a generative structure. Psenicka differs from L-System [9] based approaches because there is no prescribed interpretation to the symbols. The majority of work in L-System based music generation has focused on taking a graphical L-System grammar and reinterpreting it musically [10], [7], [16]. This approach is interesting as a theoretical exposition on the deep role of structure, and has been shown in limited cases to generate melodies similar to existing classical pieces [7]. However, in general it does not necessarily result in anything particularly musical in the popular sense.

One possible reason is that the two dimensional graphical plane and the musical space have different metric characteristics. For example, when a turtle interprets an L-System string, +/- mean rotation, mod 360 degrees. When dealing with music though, the note scale is not circular; there is a top and a bottom range to what can be heard. Although 359 degrees and 1 degree are spatially close, a note at the top of the range and one at the bottom do not sound close (where “close” means approximately the same frequency). In order to keep notes in audible range, one has to carefully author the productions [7]. Thus not all L-Systems can be played. Additionally, such a literal interpretation results in ambiguity where “left” and “right” must be interpreted the same musically; although you can go forward and back in 2D space, music only travels forward in time.

4. Arpeggio-Specific Grammar

ArpEgg follows the general approach of L-System generation but refines symbols with actions specific to the semantics of arpeggios (e.g. “advance to next note in chord”). Furthermore, it defines a number of music specific terminals (e.g. “raise by one semitone”). ArpEgg grammars are similar to, but due to these differences cannot strictly be considered, L-System grammars. ArpEgg also defines system parameters that act as input (e.g. the chord and note length for arpeggiation), and a special parameter for defining the handling of traversing the top and bottom bounds of audible notes.

ArpEgg uses context free grammars, where each production is matched independent of an element’s neighbours. Other systems [11][16] have explored context sensitive grammars for music generation but the resulting grammars are inherently more complex. This makes the authoring process harder for the artist. With this in mind, ArpEgg has focused on the more manageable space of context free rewriting rules, an area with still considerable potential for musical exploration. Furthermore, although context sensitive grammars are valuable for producing longer pieces with variety [16], this is not such a requirement for arpeggios, where repetition is common (and desirable) especially in dance music.

Similar to [9], the start symbol S is special, acting as the seed for rewriting. Rewriting proceeds, context free, to a specified number of levels. The resulting string of symbols is read by the ArpEgg interpreter.

The ArpEgg terminals are as follows:

· + : pick the next note in the chord

· - : pick the previous note in the chord

· / : add one semitone offset to current note value

· \ : lower by one semitone offset current note value

· ! : increase velocity

· * : decrease velocity

· [ : push current note context on stack

· ] : pop context from stack, make it current

· N: play current note

· _ : rest

The symbols ‘+’ and ‘-‘ are they keys to arpeggiation since they follow the chord structure. Each ‘+’ advances an index through the list of chord notes but does not play the note. Once the top of the chord is reached, the chord is raised one octave and the lowest chord note is chosen. Similarly, decreasing below the level of the first note in the chord lowers the octave, making the current note the highest in the chord. The symbol ‘N’ plays the current note. The symbols ‘/’ and ‘\’ act as semitone offsets from the current note. Current note value is thus = chordNote * octave + semitoneOffset. All notes are of the same duration, specified globally, by default 16^th notes. Rests are of the same duration. Velocity range is simplified into 12 increments from zero to maximum. When the velocity exceeds that range, incrementing and decrementing are interpreted in reverse. Thus continually incrementing the velocity will create a “hill and valley” curve. This was chosen as the most musical way to manage velocity bounds. Finally, the stack symbols ‘[‘ and ‘]’ remember and restore chord note index plus octave, semitone offset, and velocity. For example, starting with C Major (C, E, G), the string ‘N[+N/N-N]N’ would produce the following notes: C, E, E#, C#, C.

ArpEgg defines a number of global (to the grammar) settings. For ease of authoring, these are defined in the same file as the grammar. The special symbol ‘%’ is used to denote a system setting. These are:

· DEPTH: number of levels of expansion of the grammar

· DURATION: note length (e.g. SIXTEENTH, QUARTER)

· CEILING: top most octave allowed

· FLOOR: bottom most octave allowed

· BOUNDSRULE: strategy to follow when a note would be out of ceiling/floor range. Possible values are:

o CYCLE: when reaching the top of the range, start at the bottom. When reaching the bottom, start at the top. This creates the classis “Up” and “Down” arpeggio patterns.

o REFLECT: when reaching the top, interpret +/- inverted and work your way down. This creates the classis V shape of the “Up&Down” and ”Down&Up” arpeggio patterns.

· CHORD: the input chord (e.g. MAJOR, MINOR)

· ROOTPITCH: the root note pitch of the chord (e.g. C3, F#4).

Finally, the symbol ‘//’ is used to denote a comment to end of line.

5. Examples

5.1 Classic Patterns

It is relatively easy to reproduce many of the standard patterns in most arpeggiators. The BOUNDSRULE makes the patterns “Up” and “Up&Down” trivial:

// The classic Up

%BOUNDSRULE=CYCLE

S=U

U=N+U

// The classic Up&Down

%BOUNDSRULE=REFLECT

S=U

U=N+U

The pattern “Converge” from Ableton Live is also straightforward, although its grammar must be is specific to the number of notes in the chord:

%CHORD=MAJOR6th

S=N

N=N++++N---N++N-N

5.2 Example 2

A little more interesting perhaps is the grammar:

%FLOOR=2

%CEILING=7

S=+++N

N=N[-N++N]-N

With input chord C3 Major, we get the piano roll in Figure 2.

Figure 2: Example 2 Midi Piano Roll

5.3 Example 3

A strategy that tends to yield pleasing results is to construct two productions that play off each other:

%DEPTH=4

%CEILING=6

%FLOOR=2

%BOUNDSRULE=REFLECT

S=AUA

A=[N++!!N-!NB]

B=[N--N-A+*N--*N+*N_S]

U=///////

In the piano roll of the result with Chord C3 Major (Figure 3), one can spot repetition and structure (and it sounds even better than it looks!).

Figure 3: Example 3 Midi Piano Roll

Results

We will now discuss our subjective experience in using ArpEgg. It should be noted that this experience has not been validated by third party use. However, we believe its worthwhile documenting our initial experiences as a guide to further research and discussion.

It is relatively easy to come up with ArpEgg patterns that are quite listenable. We assume this is owed to the nature of arpeggios: since chord notes sound “pleasing” together, notes picked from that chord will sound pleasing. We picked arpeggios as our problem domain with the hopes of exactly this occurring. More so, with some practice, one starts to come up with arpeggios that are satisfyingly pleasing.

Some observations:

· Gaining an intuition on how to modify a grammar to achieve the desired results remains a challenge. Small changes in the grammar can have a dramatic effect on the outcome, in particular where ‘N’ is used as a source for a production. In such cases, only small values of depth (often around 3) are required to achieve fairly complex results.

· A more successful strategy seems to be in creating interrelated phrases where N is not a source for the production. The results are still very complex but are not so sensitive to change.

· Creating phrases of four notes helps ensure that the arpeggio sits in a 4/4 rhythm but requires careful use of recursion in order to preserve this property.

· A common compositional technique is scalar transposition [12]. Such inversions are trivial to construct by simply replacing note and semitone increment/decrements with their opposites, as in this inversion of example 3:

S=AUA

A=[N--!!N+!NB]

B=[N++N+A-*N++*N-*N_S]

U=\\\\\\\

· An interesting experience is listening to the exact same grammar generated at depth 3, 4, and 5. All generations sound like they belong to the same family, but the differences are difficult to describe. This is the self-similarity at work. But the subjective experience of self-similarity in music seems different than that of graphical L-Systems. For example, the experience of looking at a depth 4 Gosper curve isn’t markedly richer than that of the depth 3 expansion, whereas adding depth to ArpEgg expansions does seem to result in a different listening experience. This may partially be because of the time linear experience of music, where perception of self-similarity requires memory of sounds past, in contrast to viewing a two dimensional picture where self-similarity and structure can be taken in “all at once”.

From a practical point of view, ArpEgg can generate patterns that have enough structure to sit well in many forms of electronic music, but not so simplistic a pattern that they quickly become boring. They are interesting to listen to on their own, in a way that most arpeggio software output isn’t. There’s “just enough structure”, not too little to be boring, not too much to be chaotic.

Future

We are very interested in whether musicians can incorporate ArpEgg into their palette of electronic music tools. While we’d like to make claims regarding ease of use and expressiveness, the real test is in real usage. Presently ArpEgg creates midi files which are dropped into a sequencer, so the next step is for ArpEgg to have a live component, listening to a midi channel for chord notes and outputting a midi stream of arpeggio notes. This would further facilitate exploration, which is essential for learning.

On a more general note, we believe that most commercial music tooling provides too shallow an authoring lexicon. Whenever we see a “random” setting, we see opportunity for a generative approach to fill that gap between simplicity and randomness. However, while the conciseness of rewriting grammars brings power, it can also impede gaining an intuition on how to achieve the desired results. This problem of expressiveness needs to be better understood if rewriting systems are to be more than a novelty to artists.

Conclusions

ArpEgg is a rewriting-grammar based system that can generate both traditional arpeggios and a wide variety of new, deeply structured ones. It takes as lineage L-Systems but defines a wider set of symbols whose interpretation is arpeggio and music specific. The conciseness of rewriting rules makes exploration fast for the musician.

ArpEgg allows the musician to concentrate on the establishment of pattern, relying on the nature of arpeggios to provide an inherent tonal harmonic foundation. The self-similar structure of rewriting grammars creates intriguing, recognizable structure. This, in combination with the lack of stochastic processes, permits the artist to author rich, complex results without loss of expressive control.

References

[1] Ableton Live, http://www.ableton.com/

[2] LinPlug Albino, http://www.linplug.com/

[3] Steinberg Cubase, http://www.steinberg.net/

[4] Holtzman, S R. “Using Generative Grammars for Music Composition” Computer Music Journal Vol5, No1, pp51-64, 1981.

[5] Ming Li and Paul Vitányi. An Introduction to Kolmogorov Complexity and Its Applications, Springer,1997.

[6] Lerdahl, Fred, and Jackendoff, Ray. A Generative Theory of Tonal Music. The MIT Press, 1983.

[7] Mason, Stephanie, and Michael Saffle. “L-Systems, Melodies and Musical Structure.” Leonardo Music Journal, 4: 31-38, 1994.

[8] McGuire, Kevin. “Controlling Chaos: a Simple Deterministic Program for Drawing Complex Organic Shapes”, 3rd International Conference on Generative Art, Milan, 2000.

[9] Prusinkiewicz, Przemyslaw, and Aristid Lindenmayer. The Algorithmic Beauty of Plants. New York: Springer-Verlag, 1990.

[10] Prusinkiewicz, P. ‘‘Score Generation with L-Systems’’ Proceedings of the 1986 International Computer Music Conference, pp.455−457, 1986.

[11] Psenicka, David O. “Composing Music Based on Interaction with Self-Similar Symbolic Tree Structures”, 8th International Conference on Generative Art, Milan, 2005.

[12] Rahn, John. Basic Atonal Theory, Schirmer Books, New York, 1980.

[13] Cakewalk. http://www.cakewalk.com/

[14] Wikipedia. http://en.wikipedia.org/wiki/Arpeggio

[15] Wikipedia. http://en.wikipedia.org/wiki/Arpeggiator

[16] Worth, Peter and Susan Stepney. “Growing Music: Musical Interpretations of L-Systems”. Lecture Notes in Computer Science, Applications of Evolutionary Computing, Springer, 2005.