The Void Series - Generative Art using Regulatory Genes

Gary R. Greenfield

Department of Mathematics and Computer Science, University of Richmond, Richmond, Virginia 23173, USA.

e-mail: ggreenfi@richmond.edu

Abstract

We apply a gene regulator model to aggregations of cells in order to generate a series of two-dimensional abstract art works titled “The Void Series”. Images in “The Void Series” arise from grids consisting of two different types of cells. Cells in the grid undergo a period of morphological development following which concentrations of three of their four so-called transcription factors are interpreted as RGB color components in order to create a finished piece. Cell morphogenesis is governed by both a gene regulatory network and interactions among neighboring cells. By initially activating only the outermost cells of the grid, and by controlling for the length of time that cells are allowed to develop, we obtain an inward spiral of alive cells surrounding an inner core of dormant cells. This means an activation boundary is always present. The activation boundary reveals the changes that occur within individual cells as they undergo morphological development and symbolizes the extent to which we understand morphogenesis, while the inner void symbolizes the extent to which we do not understand morphogenesis. A genetic algorithm is used to evolve and select those images offering the greatest aesthetic impact.

1. Introduction

Although simulation of cellular processes has been previously used for artistic and scientific purposes, we are unaware of any attempts to treat the process itself as an aesthetic entity. In this paper, by loosely following a developmental model for cells based on differential gene expression that was originally formulated by Eggenberger [1], we show how to directly integrate such cellular processes into a generative system designed to yield abstract aesthetic images. Because cellular processes are simulated, the length of time for cellular development (i.e. morphogenesis) to occur becomes a key variable that can be exploited for aesthetic purposes. During the course of investigating this parameter, we were led to create a series of images called ``The Void Series.'' In addition to yielding aesthetic imagery our methods also provide insight into some of the wonders that are concealed within the inner workings of the cells themselves.

The most famous example involving modeling cellular development for aesthetic purposes arose as a consequence of the tour de force thesis of Kurt Fleischer [2]. His efforts spanned the disciplines of computer graphics [3,4], artificial life [5], and generative art [6,7]. A less well-known example by Hoar et al [8] involving modeling the life cycle of a bacterium led to images of the simulated evolution of bacteria colonies that were proffered as “creative bacteria patterns.” It is clear, however, that this work was intended primarily as a scientific visualization of bacterial evolution and that the resulting aesthetic results were merely a fortuitous by-product. While on the topic of related work, it should also be pointed out that due to the occurrence of the rectangular patterns that occur in our images, and in light of the fact his generative algorithm was used to investigate the theoretical principles underlying Mondrian's paintings, it is also worthwhile to compare our work with that of Feijs [9].

In subsequent sections we first describe our regulatory gene model for cells and then our simulation of cellular development. Next, we discuss from both a technical and artistic standpoint ``The Void Series'' that we created with the aid of a simple genetic algorithm. Finally, we present conclusions and directions for future work.

2. The Gene Regulatory Model

Following Eggenberger, we formulate a model for the cellular development of cells possessing identical genomes in such a way that differences between cells are due to regulatory mechanisms that turn genes on and off. The key idea is that segments within each cell's genome are classified as either structural or regulatory and that regulatory segments affect and are affected by immediately adjacent structural segments. Individual cells maintain concentrations of transcription factors. When structural genes are activated they yield products (morphogens) which alter the concentrations of these transcription factors. In turn, transcription factor concentrations help initiate higher order cell processes. In Eggenberger's model, depending on the type of the structural gene, besides affecting transcription factor concentrations gene products may directly initiate higher order cellular processes such as mitosis, receptor activation, etc. In our model, the products of activated structural genes only result in changes in the transcription factor concentrations that are associated with those genes, with the caveat that one of the factors exerts further control over such changes by determining whether or not neighboring cells will also have their concentrations modified. In simpler terms, in our model structural genes are in one to one correspondence with transcription factors; cells have four transcription factors; and three of the transcription factors are responsible for the concentrations of red, green, and blue while the fourth is responsible for communication between a cell and the cells in its Moore neighborhood. The activation of any specific structural gene is determined by transcription factor affinities that result from structural and regulatory gene pairings as described more fully below.

Formally, a gene is a string of eight digits

(1)

all lying in the range zero through four. A gene unit is a sequence of three genes, the first two being designated as regulator genes and the third being designated a structural gene. Each structural gene is used to define an offset and a diffusion coefficient defined by:

(2)

(3)

A cell genome consists of four gene units. A cell consists of a cell genome plus concentrations of four transcription factors (TF's). The TF's are in one to one correspondence with the structural genes. For a fixed TF and a fixed regulatory gene we extract the substring of length five from the regulatory gene beginning from the offset determined by the structural gene of its unit, then perform a base five conversion, and finally subtract the result from an environmental constant associated with the TF in order to give the affinity of that regulatory gene for that TF. Now, multiplying the affinity of the TF by the concentration of the TF, and then summing over all regulatory genes we threshold the result to determine whether the structural gene associated to the TF is excitory, inhibitory, or neutral. Note that affinities are signed quantities. Also note that in order to help implement both increases and decreases in TF concentrations we have further refined the classification of an activated gene as either excitory or inhibitory. An activated structural gene raises (respectively lowers) the concentration of the TF it influences by percent of the TF increment constant, where is the diffusion coefficient of the structural gene as that is given by (3). Further, if the TF concentration responsible for intra-cellular communication is sufficiently high, gene activation diffuses the remaining percent of the TF increment constant to the nine neighboring cells. The subtlety here is that the TF activated is not necessarily the TF whose concentration changes. In the results described in this paper the red structural gene influences the green TF, and conversely; while the blue structural gene influences the communication TF, and conversely. The rationale for this is that a cellular mechanism that leads to the activation of a gene may yield products that affect different cellular mechanisms.

3. Simulation of Cellular Development

To simulate cellular development using our gene regulatory model we arrange the cells in a grid. Edge cells of the grid are initialized with trace concentrations of each of the transcription factors while the interior cells have their concentrations all set to zero. At every time step of the development process, for each cell in the grid we perform the calculation described in the previous section to determine which genes in the cell are activated, or expressed, and then we modify the concentrations of the TF factors within the cells that are influenced by the activated genes in the manner described in the previous section. For the images shown here, only two types of cells are used in grids. One type of cell provides the substrate, while the second type - comprising only five percent of the grid - become the specialized cells. For the images shown here the grid is 50x50 whence there are 2500 cells. The number of time steps allotted for cellular development is set to 350. Since each cell is visualized as a 5x5 pixel region that is colored according to the concentrations of its red, green, and blue transcription factors, each grid yields a 250x250 pixel composition.

We embed image generation within a simple genetic algorithm (SGA). When mating cells, we use the standard one-point crossover operator and point mutation operator. To achieve image consistency we “freeze” the placement pattern of the specialty cells so that throughout each run of the SGA the specialty cells are always placed in exactly the same locations on all grids. In our preliminary experiments we used small grids with moderate population sizes and a large number of generations, but to achieve the higher resolution results shown here, we were forced to use smaller population sizes (typically 6-8) and fewer generations (usually 2-4). Due to the heavy computational load it is not possible to use an interactive genetic algorithm. This means we must formulate a fitness function. The difficult problem of designing appropriate fitness functions is still being actively investigated. For all images shown here, grid fitness is calculated using the expression

(4)

where , , , and denote the standard deviation within cells of the TF concentrations for the (C)ommunication, (R)ed, (G)reen, and (B)lue TF factors respectively; denotes the number of cells that had a change in activation status for at least one structural gene during the last developmental time step; and denotes the number of cells that are dormant i.e. the number of cells all of whose TF concentrations lie below the trace value. Thus, grids with high fitness reward images that possess variation within all color channels and whose underlying cells are still actively turning genes on and off, and penalize images that have too many black cells.

4. The Void Series

Thanks to genetic variation, in any evolving population of grids the resulting images will vary widely in the size of their inner core - the central black, or void, region of dormant cells that is activated from the outside in during the development phase. After selecting our fitness function and running the SGA more than thirty times, we culled a series of ten images – “The Void Series” - whose inner cores were all approximately the same size, whose colorings best revealed the nature of the regulatory processes, and whose compositions best revealed the aesthetic possibilities. In this section we examine some of those images.

We begin with image #2 of “The Void Series” because first, the turquoise specialized cells are clearly visible; second, the diffusion of their gene products into the immediate substrate (and no further!) is distinctive; and, third, the developmental phases of both types of cells are clearly visible at the {\em activation boundary} around the dormant inner core. Notice how the concentrations of the color components have been pushed to their maximum levels in the cells surrounding the specialized turquoise cells to form the white cells.

Figure 1. The Void Series, Image #2.

Image #3 of the series shows the opposite effect. The specialized cells have their concentrations pushed to white by a very active substrate.

Figure 2. The Void Series, Image #3.

Image #9 of the series is intriguing because of the irregularities in the diffusion patterns radiating from the specialized cells.

Figure 3. The Void Series, Image #9.

In image #1 of the series we see more clearly the developmental phases of the specialized cells because they are neatly limned in white.

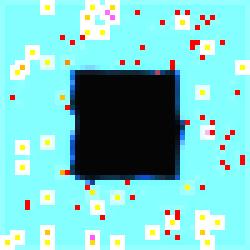
Figure 4. The Void Series, Image #1.

Specialized cell development can also be seen in image #7 of the series. Aesthetically, image #7 is also interesting because of the blurring effect that results from gene activity in the substrate.

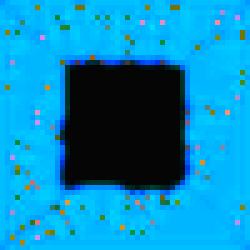
Figure 5. The Void Series, Image #7.

Image #4 of the series represents the best aesthetic result in our opinion, due no doubt in part to the naturally occurring border.

Figure 6. The Void Series, Image #4.

Image #0 in the series is the most vexing one because although its interwoven pattern of channels recurs from time to time in our evolved imagery we have no satisfactory explanation regarding its underlying cellular mechanism(s).

Figure 7. The Void Series, Image #0.

The above overly technical description of some of the images from “The Void Series” does not speak to the artistic intent of the series. The conceptual intent of these images is to initiate a dialog about cellular processes on two levels. On the public macroscopic level, by examining from a distance the inner core of dormant cells surrounded by the organized pattern of active cells, the viewer is invited to question the extent to which we truly understand the mysteries of cellular processes. On the private microscopic level, by examining from close-up the intricate and complex dynamics occurring within the cells that make up the activation boundary surrounding the inner core of dormant cells, the viewer is invited to contemplate the awe and wonder of cellular processes.

5. Conclusions and Future Work

We have presented a gene regulatory model that we used to simulate cellular processes. By associating cell products with color channel components so that the results of cellular development could be visualized, and by evolving cell genomes with the help of a genetic algorithm, we developed a technique for evolving aesthetic compositions that invites a dialog concerning our understanding of cellular processes. The compositions of these images speak to the marvels of cellular processes.

Future work could proceed in a number of directions. First, it would be helpful to try and simplify the gene regulatory model so that designing cell genomes could be done on a more intuitive basis. Second, additional effort should be devoted to trying to understand why metrics for evaluating aesthetic fitness are, or are not, successful. Third, results obtained by initializing grids in a more organized fashion, as opposed to just randomly sprinkling in a few specialized cells, should be explored. For example, using one cell type for a “nucleus” and a second cell type for a surrounding membrane could prove worthwhile. Fourth, modifying cell genomes dynamically over the course of the cellular development cycle might lead to novel imagery. Fifth, it would be interesting to experiment with additional transcription factors: either visual ones, such as opacity to use for compositing against a background image, or physical ones, such as toxins that could induce more catastrophic cell changes.

References

[1] P. Eggenberger, Evolving morphologies of simulated 3d organisms based on differential gene expression, Proceedings of the Fourth European Conference on Artificial Life (ECAL97), 1997, 205-213.

[2] K. Fleischer, A Multiple-Mechanism Developmental Model for Defining Self-Organizing Structures, PhD Dissertation, Caltech,

Department of Computation and Neural Systems, June 1995.

[3] K. Fleischer et al, Cellular texture generation, Computer Graphics Proceedings, Annual Conference Series, 1995, ACM SIGGRAPH, 239-248.

[4] K. Fleischer, Cells: Simulations of Multicellular Development, animation shown in Siggraph 94 Electronic Theatre, in Siggraph Video Review, 1994.

[5] K. Fleischer, Investigations with a multicellular developmental model, Artificial Life V Conference Proceedings, 1996, 229-236.

[6] K. Fleischer, Spike, computer image exhibited in ACM Siggraph 95 Art Gallery, in Siggraph Visual Proceedings, 1995.

http://www.siggraph.org/artdesign/gallery/S95/Fleischer.html

[7] K. Fleischer, Who's Driving? Control Issues for Generative Media, keynote presentation, First Iteration : a conference on generative systems in the electronic arts, CD-ROM “D”, Dorin and McCormack (eds), Melbourne, Australia, December, 1999. http://www.csse.monash.edu.au/~iterate/FI/confProgram.html

[8] R. Hoar, J. Penner, C. Jacob, Transcription and evolution of a virtual bacteria culture, 2003 Congress on Evolutionary Computation Proceedings, IEEE Press, 2003, 54-61.

[9] L. Feijs, Divisions of the plane by computer: another way of looking at Mondrian's nonfigurative compositions, Leonardo, Vol. 27, No. 3, 2004, 217-222.