Interactive Organic Art

R. Behravan, MSc.

Department of Electrical Engineering and Computer Science, University College London, London, England.

e-mail: r.behravan@ee.ucl.ac.uk

R. Carlisle, BA.

Glassworks Ltd. Visual effects and post production, London, England.

e-mail: robin@glassworks.co.uk

Abstract

In this paper we explore the use of sound to interact with the artificial biological patterns based on reaction-diffusion systems. Modelled by relatively straightforward cellular automaton, reaction-diffusion systems can seem alive and interaction with such systems through touch, sound and music creates an organic, fluid and non-repeatable aesthetic experience.

The aim of our system is to use reaction-diffusion to create an aesthetic accompaniment to music, for use in applications such as art installations and music venues. With an appropriate mapping from music to reaction-diffusion, we aim to translate some of the emotional content of sound into visuals, enabling an investigation of how changing patterns in different media affect us emotionally.

1. Introduction

In his paper “chemical basis of morphogenesis”, Alan Turing devised a system to model biological development and pattern formation [9]. Reaction-diffusion systems are based on the communication amongst cells by the way of chemicals. It is an attempt to explain symmetry breaking and pattern formation in the early embryo, generating growth. These mathematical systems can be utilised to generate two-dimensional organic patterns resembling stripes on zebra skin or spotty patterns seen on fish skin.

In this article we will describe the science of reaction-diffusion while exploring the aesthetic values of interacting with such systems using sound and touch. However the beauty of reaction-diffusion systems should not let us forget the importance of the fundamental biological questions that they might be able to answer.

In the first part of this article we will explain the background and the tools we need to implement our system. We then explain the system and its method of visualization. In the last section of this article we will discuss the motivation behind the usage of science and mathematics in creating art.

2. Background

2.1 Reaction-Diffusion and Pattern Formation

2.1.1 Biological Development. How does a highly organized body plan emerge from a single cell? This is one of the most fundamental questions in developmental biology. Development is the emergence of organized structures from an initially simple group of cells [4]. In 1952 Alan Turing proposed a hypothetical chemical reaction that could spontaneously break the symmetry in an initially uniform mixture of chemical compounds, leading to stable spatial patterns [9]. He was hoping that this would provide a model for how patterning takes place in an initially homogeneous fertilized egg. He called these chemicals morphogens – intending to convey the idea of form producers [8].

2.1.2 Reaction-Diffusion. Reaction-Diffusion systems are pattern generating, self-organizing complex systems that hope to model the initial stages of biological development. These systems are based on cell communication by the way of interaction of two or more chemicals.

Diffusion is the action of spreading of morphogens and Reaction is the process that creates and destroys morphogens, based on their concentration in each cell [10]. In Turing’s chemical system, diffusion is competing with autocatalytic and inhibitory chemical reactions [5].

2.1.3 Mathematical Model. Reaction-diffusion systems are modelled by the partial differential equations where the rate of change of each chemical depends on some function of reaction plus some function of diffusion.

da/dt = F(a,b) + D_aѲ a

db/dt = G(a,b) + D_bѲb

Where da/dt and db/dt describe the rate of change of chemicals a and b, with respect to time. The Laplacian operator applied to a or Ѳa is the measure of how high the concentration of a is at one location with respect to the concentration of a nearby (its neighbours). Ѳb is the measure of how high the concentration of b is at one location with respect to the concentration of a nearby b. D_a and D_b represent the diffusion rate of chemicals a and b and F(a,b) and G(a,b) are some reaction function of chemicals a and b.

Although Turing was the pioneer of this discipline, others have devised other reaction-diffusion systems, the most important of which are the Meinhardt and the Gray-Scott systems. The three equation systems are provided below:

Turing Equations.

da/dt = D_aѲ a + s (16 – ab)

db/dt = D_bѲb + s (ab – b –b)

Where the parameter s is the reaction speed and b is the source of slight random irregularities in chemical concentration [9].

Meinhardt Equations.

da/dt = D_aѲ a + s (a² / b + b_a) – r_aa

db/dt = D_bѲb + sa² + b_b - r_bb

Where the parameters b_a and b_b are basic activator and inhibitor production and r_a and r_b are rates of decay or removal of chemicals a and b and s is the source density [6].

Gray-Scott Equations.

da/dt = D_aѲ a – ab² + F(1 – a)

db/dt = D_bѲb + ab² + b(F + K)

Where the parameter K is the dimensionless decay rate of the reaction and F represents the rate of the process [7].

Analytical solutions for differential equations are not always possible and that is why we seek discrete numerical techniques.

2.2 Cellular Automata

A Cellular automata is a one, two or three-dimensional grid of cells in which the fate of a cell or its rate of change with respect to time is determined by the states of its neighbours through a set of local rules. Cellular automata provide simple and discrete mathematical models and can act as good models for biological and physical phenomenon [2].

To model reaction-diffusion systems using two-dimensional cellular automata, each cell starts with a certain amount of chemicals a and b. The Laplacian Ѳa refers to how much of a chemical a cell contains compared to its neighbours. By neighbours we mean cells on the top, bottom, left and right.

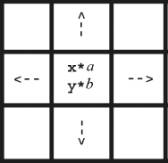
Figure 1 represents a small section in a cellular automata.

The cell in the middle contains a certain amount of chemical a represented by x*a and a certain amount of chemical b, y*b.

The arrows represent the neighbouring cells.

Fig. 1

This is to provide the information for the update of the chemical amount in a cell relative to its neighbours. The value of the reaction function is then calculated which depends on the amount of chemicals a and b in that cell. The amount of chemicals a and b in all cells can then be updated simultaneously by evaluating and adding da/dt and db/dt to the amount of a and b in each cell using any of the above equations.

2.3 Visualisation

An example of how to visualise such a system using computer graphics, is to create an imaginary grid of cells, each of which would contain a certain amount of chemicals. Each chemical would be specified its own colour. A pixel would represent a cell whose colour is the combination of the colours of the chemicals in that cell.

2.4 Interaction

The mathematical equations of Turing, Meinhardt and Gray-Scott can be manipulated to create different results or patterns by varying the values of parameters. For example the size of the spots created by the Turing equations are dependent on the value of s, the larger the value of s, the smaller the spots. Figures 2 and 3 have been generated using the Turing equations. S has a larger value in Figure 2 than it has in figure 3.

Fig. 2 Fig. 3

In the Gray-Scott equations by varying the amount of k, we can turn spots to stripes and vice versa. Figures 4 and 5 were generated using the Gray-Scott equations; K has a larger value in Figure 5 than it has in figure 4.

Fig. 4 Fig. 5

By allowing the change in the value of a parameter, for example the size of the spots, to correlate with the change of another variable, for example the volume level of a piece of music or a human voice, we can create interactive audio-visuals.

2.5 Sound

Sound is a wave which is created by vibrating objects and propagated through a medium from one location to another. The simplest kind of pressure wave is a sine wave. Figure 6 shows the air pressure against time or the sound wave of 1/20 seconds of a piece of music.

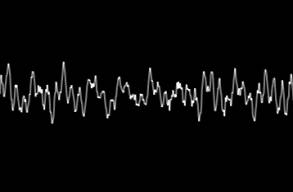
Fig. 6

Fourier transform is based on the idea that any wave can be expressed as a sum of sine and cosine waves. Using Fourier transform, we can decompose a signal or a (sound) wave to its component frequencies. Figure 7 represents the graph of frequency against amplitude of the same 1/20 seconds, represented in figure 7.

Fig. 7

The decomposition of sound will allow us to manipulate parameters in reaction-diffusion systems by relating them to the subunits of sound. This will also allow us to change the colour of the visuals we are creating according to the frequencies of sound, representing interaction.

2.4 Generative Art

In this work we use the definition of generative art proposed by Philip Galanter:

“Generative art refers to any art practice where the artist uses a system, such as a set of natural language rules, a computer program, a machine, or other procedural invention, which is set into motion with some degree of autonomy contributing to or resulting in a completed work of art.” [3]

Generative art can be used as a method for developing ideas and as an aid to human creativity. This is an area of art in which the outcome is unpredictable. Moreover the end or the final result is not necessarily an issue, unlike other areas of art. We will now review a few generative artists and their work.

Mauro Annunziato is a scientist and also an artist working in the area of artificial life and the application of complexity to art. He uses chaotic, self-organizing and complex systems together with genetic algorithms to create interactive audio-visual installations.

Philip Galanter creates various kinds of generative software and hardware systems. In his most relevant work to this article, self-organized drawing, he uses reaction-diffusion systems to generate the macrostructure and then uses genetically based software for the generation of the microstructure of the drawings [3].

Daniel Bisig has created a sound interactive growth art installation called BioSonics, which transforms the user sound interactions, into spatial and temporal patterns. In this system, sound is converted into chemicals, which cause the dynamics in the chemical reactions to change leading to the growth processes [1].

David Fried has created a series of interactive sound-stimulated sculptures called self-organising still life in which solid spheres interact with one another and are also stirred into motion by ambient sound[1].

3. Interactive Organic Art

The tools we need to implement our system are two-dimensional cellular automata for generating two-dimensional patterns, a suitable reaction-diffusion system and a suitable way of interacting with sound.

Reaction-diffusion system. In our experiments with all three systems of reaction-diffusion, we came to the conclusion that the Gray-Scott equations are the most appropriate for real-time interactivity. This is because in the Turing and Meinhardt systems, we start with a grid of cells in a cellular automata, all of which are then allocated the same amount of chemicals a and b plus a certain amount of randomness in the chemicals. Then using the equations, the amount of chemicals in each cell is updated, and in doing so, a process of self-organisation and refinement begins and patterns start to emerge. Turing and Meinhardt systems converge to a solution, a final result, whereas the Gray-Scott equations, with the right parameters can be highly dynamic and unpredictable and create non-repeatable non-stopping patterns.

In the Gray-Scott system, all the cells are initialised with no amount of chemicals and then a small amount of perturbation is introduced to a small area of the grid. Using the mathematical equations to update the amount of chemicals in each cell, the area of small perturbation begins to grow in a fluid, life like manner. This fluidity allows the sensation of interaction by touch or a mouse in the way of changing the amount of chemical in the cells that are touched with a mouse. Also the speed of changing from one pattern to another allows the interaction with touch or a mouse or sound using Gray-Scott equations, very effective.

Another reason to use the Gray-Scott equations is the range of value for certain parameters which make the system very chaotic, creating volatile patterns generated by the birth and annihilation of patterns. This volatility of the system will allow us to create never-ending visuals. This non-stability is not chaotic enough to seem random and is not ordered enough to seem uninteresting. It is somehow unpredictable but always familiar; similar to fire, clouds and lava lamps. It reminds us of the idea of the edge of chaos, an interesting area complexity theory where interesting solutions exist.

Visualisation. The two-dimensional cellular automata that we used for our experiments can be represented as a set of cells or points flat on a two-dimensional grid or they can be mapped on to a three-dimensional surface a sphere for example.

In computer graphics many three-dimensional models are represented using polygons. If we think of the surface of a any three-dimensional computer model as a set of points each of which having a certain amount of some chemicals represented by some colours, we can run reaction-diffusion systems onto any kind of surface and not just a flat two-dimensional model.

For our purposes we use three-dimensional models created with triangles like the sphere shown in figure 8. Figure 9 shows the use Gray-Scott equations on the geodesic sphere.

Fig.8 Fig. 9

Sound Interaction. Our system combines two-dimensional cellular automata modelling reaction-diffusion, synchronised by the real-time fluctuations of audio volume input to the system. Frequency (pitch) derived from Fourier transform is used to determine colour of emerging patterns. In some of our experiments we have allocated reddish colours for deeper sounds and bluish colours for higher frequencies. Also the size of the patterns change according to frequency and volume, smaller patterns for higher frequencies and volume and larger patterns for lower frequencies and volume. This method can loosely be used to reflect ones mood by the changing colours and patterns according to the volume and the frequency of ones voice. User interaction (keyboard and mouse) enables reaction-diffusion parameters to be altered, causing a user-determined “flow” of patterns.

By decomposing the sound wave in to its component frequencies using a Fourier transform, we basically create many waves, each of which can be linked to a parameter in a mathematical system for example a reaction-diffusion to vary the value of that parameter. Moreover the range of the value for a parameter in a reaction-diffusion system can be changed according to the range of the volume of the sound of interaction.

4. Conclusion

The main aim of this article was to introduce the basic ideas and methods for generating organic visuals using computer graphics and also an introduction to use of sound for interaction with any multi-parameter system. It is important to realise the importance of mathematics and science in creating systems such as the ones described in this paper. Also it is important to note that mathematics can be used not just for abstracting scientific concepts but as a tool for creation of art. Moreover none of this work would have been possible without the use of computers and computer graphics. We live in a very exciting time of digital revolution where we can put most ideas in to the practice using computers.

None of our artwork has been shown in this paper. For the purposes of this article, we intended to introduce the reader to the tools and to encourage them to use their own creativity and imagination to create their own interactive computer art. However the interested reader will be able to see our artwork on the following website http://www.hoohar.com/ramona/ .

References

1 ) Bisig, D., 2003. BioSonics – Interactive Growth System. In proceedings of the sixth Generative Arts Conference. Milan: Italy.

2 ) Camazine, S., Deneubourg J. L., Franks N. R., Sneyd J., Theraulaz G., Bonabeau E., 2003. Self-Organization in Biological Systems, New Jersey: Princeton University Press.

3 ) Galanter, P., 2003. What is Generative Art? Complexity Theory as a Context for Art Theory. Interactive Growth System. In proceedings of the sixth Generative Arts Conference. Milan: Italy.

4 ) Lewis, W., 2002. Principles of Development, New York: Oxford University Press.

5 ) Meinhardt, H., 1982. Models of biological pattern formation, Germany: Academic Press.

6 ) Meinhardt, H., 1995. Algorithmic beauty of sea shells, Germany: Springer, third edition.

7 ) Pearson, J. E., July 1993. Complex patterns in a simple system, Science, 261,189.

8 ) Saunders P. T., 1992. Collected works of A..M Turing: Morphogenesis. Amsterdam, Holland: North Holland.

9 ) Turing, A.M., 1952. The chemical basis of morphogenesis. Philosophical Transactions of the Royal Society London: B327, 37-72.

10 ) Turk, G., July 1991. Generating Textures on Arbitrary Surfaces Using Reaction-Diffusion. In proceedings of SIGGRAPH conference, Computer Graphics, Vol. 25, No. 4, pp. 289-298.

---

[1] http://www.galerie-poller.com/