Architecture: Forme, Space and Order?

Marie-Pascale Corcuff

DIPAU, Ecole d'Architecture de Bretagne

COSTEL (LETG UMR CNRS 6554) Université Rennes2, France

e-mail: mp.corcuff@rennes.archi.fr

Abstract

This paper begins with a reminding of the links between architecture and geometry and of the main theoretical concepts of classical geometry. Then, the concepts of fractal geometry are approached, to demonstrate how fractal geometry contains and extends classical geometry. Last, a practical model for fractals (IFS) is described, and, through a few experiments, it is shown how this model may be a generative model for architecture.

Introduction

Our research team, DIPAU (didactique du projet architectural et urbain: didactics of architectural and urban project), is composed of eight teachers of the Ecole d'Architecture de Bretagne. Four of them work on the design process, the other four on the problematic of form processes. This paper is relative to the work of this last sub-team, whose members are an architect who teaches computer science (myself), an historian of landscape and garden art, an architect-engineer, and a sculptor. Our interest is in form as result of a process, in the context of architecture teaching. We consider that it is important to discuss the notion of form, even if it is not the only entry point in teaching architecture, because otherwise students may be tempted to rely only on referential architecture without understanding the true nature of form. This study of form implies many disciplines which take part in the formation of architects, mathematics as well as art, engineering as well as history, etc. Teaching architecture implies new ways of looking at natural forms, and new operations on space and form. Our aim is to explore the theoretical questions relating to the notion of form through the evolution of geometry, as well as to design new tools for teaching architecture, not recipes to produce architectural forms, but didactic proceedings which aim to change the way students look at forms, and provide them with augmented means to consider form, space and order.

1. Architecture and classical Geometry

Architecture and geometry have entertained for hundreds and even thousands of years a very special relationship. Architects of our generation were trained with the concepts of space, form and order as described for example in the famous book by Francis D. K. Ching, Architecture: Form, Space and Order, which implies the context of classical geometry. In this book, form is defined relatively to “primary” shapes, which are the so-called geometric shapes, specifically the circle, the (equilateral) triangle and the square (“The simpler and more regular a shape is, the easier it is to perceive and understand” [1]) and to platonic solids generated by those shapes, i. e. the sphere, the cylinder, the cone, the pyramid, and the cube. Ching refers to Le Corbusier to comfort this choice: “… cubes, cones, spheres, cylinders, or pyramids are the great primary forms that light reveals to advantage; the image of these is distinct and tangible within us and without ambiguity. It is for this reason that these are beautiful forms, the most beautiful forms.” [1]. It is interesting to see that Ching, following Le Corbusier, refers to these forms by way of our perception (and our understanding), because what has geometry to do with our perception? Geometry is not a natural science, as, if we exclude astronomy, there are not much geometrical natural forms… If we admit that our perception has been set in prehistoric ages, even in pre-human ages, it had nothing to gain in recognising geometrical forms, it did not help us to fight wild animals or recognise good food, etc. Then why do human beings (even very young, and probably though animals do not) perceive geometrical forms (even if this geometry is approximate) as different from not-geometric ones, why do they feel them as adequate, and even beautiful?

Underlying the essence of these “geometric” forms are the linear transformations, i. e. translation, rotation, symmetry and scaling. The triangle, the square and the circle have respectively 3, 4 and ¥ axes of symmetry, as well as the same number of rotation symmetries. It can be noted that the smallest number of symmetry axes is not a caution of simplicity: if we transform the circle into an ellipse, this number falls from ¥ to 2 (with no more rotation symmetry), but the circle is felt as more regular, more simple than the ellipse. The biggest is not more of a caution, as the examples of the triangle and the square show us. Counting the number of symmetry axes is then certainly not the way our “perception” tells us that a form is a good, geometric one. But we are nearer from what must be at the core of the question, because it has certainly to do with, not observation, or not only that, but action. We can translate, rotate, return a shape (as to squeeze or extend it, it is more difficult, but we know that the same shape looks smaller when it is farther from us), we have done that a lot of times, and we can imagine what becomes a shape under those transformations, and guess if it will be identical or not. But is it really what draws us to geometric shapes and forms, and what makes us recognise them?

Those famous primary shapes can be drawn using only the instruments directly linked to the group of linear transformations, i. e. the compass and the rule. The linear transformations are also implied in the complexification of form, in its transformation, its composition, such as architects have done in all those centuries. This leads us to a better understanding of the link between geometry and architecture. One could think that architecture has used geometry because it was a sort of transcendental science, something of a higher level which had to be respected in order to attain harmony and beauty. But we can also think that geometry, which has not a lot to do with observation of natural forms, owes to the propensity of man to make, to build, to draw. There are not many straight lines in nature (apart from rays of light), but if one puts a cord between two poles, or between two trees (or even between one's two hands), one will tend to pull it straight, and this straight line will appear more adequate than the loose one. In the same way, a wild goat will wander randomly when grazing, and the part of grass eaten by it will not have a definite geometric shape, but if you tie it with a cord to something, it will graze a beautiful filled circle… Man, by its making, adds to nature a lot of geometric forms, not in awe to geometry, but because it is often the easiest way of making things.

At the core of classical geometry, lies the concept of dimension. This notion is a topological one, which can be defined by recurrence. If we admit that a point is of dimension 0 (axiom), then a line is of dimension 1 because a point defines a “frontier” on the line, i. e. one cannot trespass the point to reach the other part of the line. In the same way, a line will define a frontier on a surface, which will be of dimension 2, and a surface in a volume (dimension 3), and we can imagine what would be a 4-dimension form, though our perception is limited to 3 dimensions, as Henri Poincaré proved very clearly. A line may be generated by translating a point in one direction, a surface by translating a line in a second direction, a volume by translating a surface in a third (and last) direction. A fourth direction has to be dependant on the three first ones, in our 3-dimension space. Point, line, surface, volume, have lead our way of thinking of space, in the realm of architecture as well as of art (Kandinski). This topological notion becomes a metric one when one defines measure and 3 axes along which to develop the 3 directions. About this question of axes, we must point the fact that the body of man is not a geometric form, but that it has an approximate plane of symmetry (left/right), and is highly driven by verticality (gravity) as well as by the rear-front axis. The three axes (x,y,z) come naturally from this disposition. Either topological or metric, this concept of dimension as an integer number implies that there is a gap between the different dimensions. Even if a line may be generated from a point, as soon as you begin to translate the point, it becomes a 2-dimension form.

It is obvious that architecture, for centuries and millennia, had much to owe to classical geometry, that those two fields have grown together, have even nourished each other. But both stumbled over what was named irregularity, disorder, complexity, etc. The word “informal” shows the limits of classical geometry. Anything that can be named or recognised is form or has a form, obviously, and calling it “informal” simply means that our geometric tools for describing it are not adequate. Architecture was attracted to natural forms as nature (as another name for God) was supposed to make perfect forms. But what could it understand of natural forms through its timeless ally, geometry? Natural forms were considered by geometry only if they were kind enough to yield to its laws: crystals were geometrical man's pets, for example, though who has seen actually one of them in his daily life? Clouds, mountains, trees, leaves, grass, etc. were not so complacent, and geometry had given up on them, till Mandelbrot came with fractal geometry.

2. Fractal Geometry

First, what is a fractal? A main example is the von Koch curve: you take a segment, you cut it in three, you replace the middle segment by the two segments which form an equilateral triangle with it, you do the same on the four segments obtained, and so on…

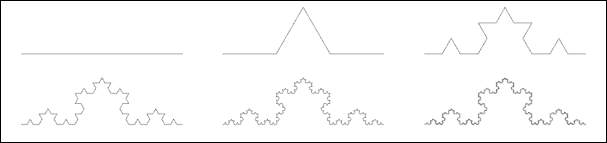
plate 1: the step by step construction of the von Koch curve

“And so on” means that you do that an infinite number of times: you define a recursive process, and this is the key-word about fractal versus classical geometric forms. Actually you don't go till infinity, and even the computer which you use doesn't either… Because it is impossible. You stop when the resolution of your computer screen or of your printer yields a good approximation of the ideal result (that is, when your result is not much different from the one obtained with one more step). But you never draw a line or a circle either: mathematic objects are ideals; representation is always an approximation. Returning to our von Koch curve, we know that it has paradoxical qualities: its length is infinite (as it is multiplied by 4/3 at each step) while it stays in a bounded area. That is not possible in classical geometry.

Actually, the main characteristics of this curve is its dimension. Fractal geometry provides us with another definition of dimension. If a figure is what is called “self-similar”, i. e. if it is made of parts which are similar to the whole though at a smaller scale, then we find what we'll call its “fractal” dimension by dividing the logarithm of the number of parts by the rate of the scaling (if it is the same in all the parts, which is the simplest case). The von Koch curve is self-similar, it is made of 4 parts which are similar to the whole, 3 times smaller: its fractal dimension is then equal to ln 4 / ln 3 = 1,26186… (actually we could say also that it is made of 2 parts which are similar to the whole by a scaling of 31/2 so d = ln 2 / ln (31/2) = (2 ln 2) / ln 3 = ln 4 / ln 3 ,which is the same…).

Plate 2: self-similarity of the von Koch curve and of the segment

But a segment is self-similar, too. It is made of 2 parts which are similar to the whole by a scaling of 2: the result is obvious, d = ln 2 / ln 2 = 1. The fractal dimension is then coherent with the topological one. We can say that a form is a fractal if its fractal dimension differs from its topological one. It teaches us that fractal geometry is not a non-euclidean geometry, but that it contains and extends classical geometry.

Extending classical geometry, fractal geometry manages to cross the gap that exists between the topological (integer) dimensions. In the case of the von Koch curve, the fractal dimension is directly linked to the angle α with which we make the “peak” in the middle: d = (ln 4)/(ln (2(1+ cos α))); when α equals 0°, we have a segment (d=0), when α equals 90° then d=2 (and in the end of the process, the line fills completely a triangle: it becomes a surface); in between, we can travel continuously from the line to the surface.

Plate 3: von Koch curves from dimension 1 to dimension 2

We can imagine ways to travel from point to line, and also from surface to volume. We could even imagine ways to travel from volume to 4-dimension “hyper-volume” and so on…

The first example we saw, the von Koch curve, is one example of a recursive process of “folding” a line. There are lots of similar processes (the Peano curve, which fills a square; the Hilbert curve, which we can even extend to filling a cube), you can also fold a surface (and wonder what would mean to fold a volume…), all of which augment the dimension. Another kind of process allows us to diminish the dimension of a given form. An example is the Sierpinski triangle: you start with a filled equilateral triangle, and you remove the similar triangle which is in the middle; that leaves three triangles on which you repeat the process, and so on.

Plate 4: the step by step construction of the Sierpinski triangle

In this case, we have a form which is made of 3 parts which are similar to the whole with a scaling of 2: d = ln 3 / ln 2 = 1,58496…, while a filled equilateral triangle is made of 4 parts which are similar to the whole by a scaling of 2: d = ln 4 / ln 2 = 2, which is what we expected of a surface!

Plate 5: self-similarity of the Sierpinski triangle and of the equilateral triangle

Recursively making holes in a surface provides us a way to diminish its dimension. It is obvious that we can also make holes in a line (Cantor) or in a volume (Menger). But those ideal fractals are not much irregular, actually they are as ordered as classical geometric shapes or forms, since they share with them the classical axes of symmetry (one for the von Koch curve, three for the Sierpinski triangle), and show a symmetry of another type: self-similarity (which we see in some geometrical forms such as the segment and the equilateral triangle, but not, maybe, in all of them). And it is obvious that they do not look like any known natural form…

In order to obtain more look-alike natural forms, it is generally admitted that the best way is to randomise the process. A very simple way of randomising the process of the von Koch curve consists in choosing by way of “heads or tails” the side on which the peak will be done on each segment. It's a very weak randomness, but it is very controllable, and it doesn't change the fractal dimension, since statistically the form remains self-similar. We may do the same when folding a surface, but we can also augment the randomness in allowing the displacing of points at each step to be chosen inside a continuous interval: it is a good way of simulating something like a “relief”, mountains which may be more dramatically exhibited if you cut them by an horizontal plane, which highlights the complexity of a wild coast, and reveals islands, peninsula, isthmuses, etc.

Plate 6: randomised recursive folding of a plane

Likely, you can introduce randomness in a recursive holing in applying what is called curdling, and you obtain what is called a fractal dust. In all of these examples, randomness is totally controlled, and generally the fractal dimension is statistically conserved. All those examples, and there are many others, show why fractal geometry has been so efficient to simulate natural forms, and may have been associated with everything that is irregular, disordered, and even informal. However, it is not compulsory to use randomness in order to obtain complexity, as we'll see later.

3. Architecture and fractal geometry

What is the use of fractal geometry for architecture? Indeed, natural forms are really the results of processes: organic ones grow, even inorganic ones like mountains or clouds are not “made” as they are at the time we see them, they have also somewhat “grown” through a process of their own. No natural form stays as it is from beginning to end. We are not always aware of that process because the time rate may be so that in one human life, or even in many of them, the changes may not be felt: for example, the continental drift was unknown till recently, and even some trees, moreover mountains, may seem to have always been are they are now. But we are used to see a lot of natural forms (clouds, plants, etc.) evolve through a very faster time rate, and we can admit that they are all the result of a process. So, it is not strange to simulate them through a process, even if this process is not exactly, or not even the same at all, as that which has actually generated that form. But forms made by man do not grow, they are built, assembled, sculpted, etc. That is a little less true for urban forms, which is a sense “grow” too, and are not totally “made” at a time, but evolve through a process a little similar to those of natural forms. But architectural forms are the archetypes of built, assembled, forms, and, if they may be decaying after they are built, they are not generally designed to evolve, as shows the money we put in their renovation. So, what is the use of processes such as recursive folding and holing for architecture?

First, we must stress the point that folding and holing are not foreign to what is actually the making of architecture. In his first sketches of a project, to define an envelope, an architect may draw a line around a surface, and then “fold” it to yield to the necessities of the functions, to allow a better access to light, etc. Another way architects use when they begin to work, is to start from a volume, and then holing it, digging into it, to define different inside spaces. Generally, those actions are not recursive processes, or at least they have not been seen in that light. But the point is that the “actions” we have described are part of the design process, which doesn't rely automatically to the actual building, but is more abstract, these actions are actions of the mind, not yet those of the mason. The design process may use wider, richer means than the building process. As fractal geometry is not an alternative to euclidian geometry, but comprises and extends it, and as it is effective in the description and understanding of natural forms (with which architecture has always confronted itself), the architectural design process may be enriched by its concepts. The geometrical tools of the architects may extend themselves to those new tools, which are processes, and it is possible because architects use computers, which are the only tools that can really go through these processes. Sadly, architectural computer tools dedicated to architects do not provide them with other tools than the classical ones. We have to imagine tools which will help architects to design forms which are no more static ones, but which are the result of processes.

But, first, we must go further in describing the actual means of making fractals. Recursive folding and holing seem to be very different ways of dealing with forms. But there is a way to look at the results of these processes, i. e. the fractals themselves, which gathers them under the same theory. This theory is the theory of IFS (iterative function system [2]) which demonstrates that any fractal is an attractor for a set of a number (generally a small number) of contractive transformations. These transformations may be linear (combinations of translation, rotation, symmetry and scaling) or affine. If we look at the way in which a figure is self-similar, we can easily find the transformations that compose the set, because they are the transformations that lead to each of the different parts of the form. In the case of the von Koch curve, as well as in that of the Sierpinski triangle, they are linear. The translation, the rotation angle and the scaling rate are easy to determine. There are two algorithms that will lead to the fractal, and they both transcribe the fact that the fractal is an attractor: in the first one, the deterministic algorithm, you start with any set of points (pixels) and apply to it the set of transformations, and then apply to the result again the same set, and so on, and you will always end with the fractal itself. You may either simulate the actual definition of the von Koch curve or of the Sierpinski triangle by starting respectively with a line and with an equilateral triangle, or transform a weird set of points, or start from a single point, which is the way to obtain the neatest result (it is not the best way if the transformations have not got the same weight, though the results are interesting anyway).

Plate 7: a fractal as attractor of an IFS, starting from anything

In the second one, the stochastic algorithm, you start with a single point (any point), and you apply to it any of the transformations chosen at random, and then you do the same to the point you have obtained, and so on. The randomness that appears in the process has nothing to do with the one we discussed earlier. Actually, the definition of the IFS is in both cases deterministic, it is only the way in which you apply the definition of an attractor which differs. In both algorithms, you may affect a colour to the point relative to the transformation applied to it, and you obtain the decomposition of the fractal accordingly to its set of transformations.

Without going further into this question, we can admit that IFS can be used as the most general way to generate fractals. The freedom with which we can choose the set of points at the start of the process, provides us with a lot of initial steps which are interesting in themselves, even if they are not strictly fractals. For example, if you start the deterministic algorithm with a line, you can simulate L-systems, even branching ones.

Moreover, you can take a form and guess the IFS that will have an approximation of this form as attractor. In order to achieve this result you try to cover this form by a number of duplicates of itself which you contract, translate and rotate (if you look for similarities). You make what Barnsley calls a collage and the parameters of these transformations of the initial form will give you the contracting rates, translation vectors and rotation angles of the transformations that will compose the IFS. The better the collage is (with not too much holes nor superpositions), the more the IFS will approximate the form.

Let's take an example with a leaf and let's run the stochastic algorithm: though the leaf is not really the same, it is a rather convincing leaf. To obtain an autumn leave, you change the colour of each pixel according to the times this pixel has already been targeted.

Plate 8: from real leaf to autumn leave (stochastic algorithm)

	rate	angle	dx	dy
w1	0,6	0°	0	0
w2	0,6	0°	0	0,7
w3	0,7	60°	-0,125	0,2
w4	0,7	-60°	0,125	0,2

Table 1: parameters for the leaf

The IFS for the leaf gives us a structure (4 transformations) and parameters. If you change a little those parameters, you get various leaf of the same structure, but a little different, as is the case for real forms.

Plate 9: a handful of autumn leaves

This shows us how IFS may be generative, i. e. we can manipulate the parameters of the transformations in order to generate different kinds of forms inside a given structure. To describe the overall abstract structure of the IFS for the leave we may consider that it is constituted of four parts that radiate from the centre. One of them is reversed in direction, though. If we implement the most regular IFS according to this structure, we obtain a not-fractal shape, an L-shape.

	rate	angle	dx	dy
w1	0,5	0°	0	0
w2	0,5	0°	0	0,2
w3	0,5	90°	-0,2	0
w4	0,5	-90°	0,2	0

Plate 10: IFS for the L-shape Table 2: parameters for the L-shape

By changing the contracting rate, and then the number of transformations, we can obtain various interesting fractal forms deriving from this last L-shape.

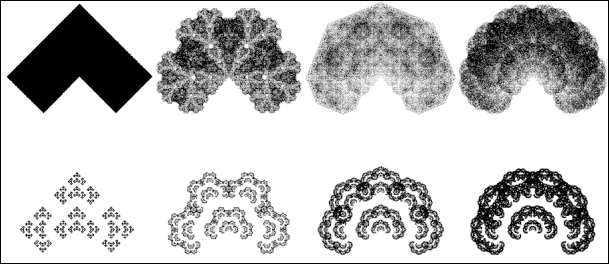
Plate 11: variations of the L-shape

Exploring this structure, we may come, by successive approximations, to a configuration that reminds us of an African architectural configuration that Ron Eglash [3] has revealed as fractal, the ba-ila settlement.

Plate 12: an approximation of a ba-ila settlement

Returning to the initial structure we may choose to not reverse one of the parts and explore the IFS constituted of a central part, and a number of parts radiating from this centre.

Plate 13: varying the number of parts of a radiating IFS

This structure may remind us of very different kinds of architecture, and we may turn to sketches of ideal churches by Leonardo da Vinci, the structure of which has generally an order-8 symmetry.

Plate 14: results of the deterministic algorithm for an 8-part IFS, starting from a square

Using the freedom we have to start from any set of points, we can make different experiments, for example starting from an octagon, with a 9-part IFS (8 parts plus 1 in the centre):

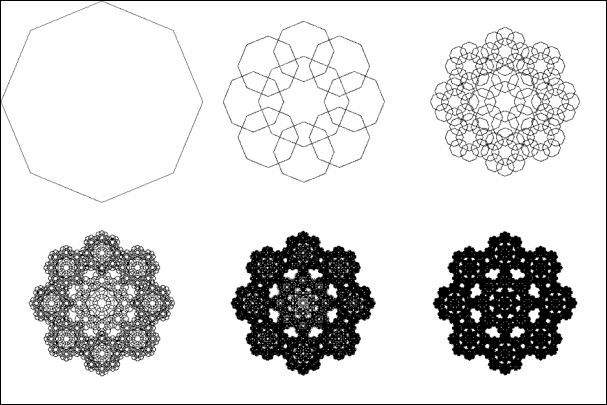
Plate 15: results of the deterministic algorithm for a 9-part IFS, starting from an octagon

Some sketches by Leonardo are rather founded on the symmetry of the square than on that of the octagon. We can also explore this structure.

Plate 16: : results of the deterministic algorithm for an 8-part IFS, starting from a square

Conclusion

In this paper we have put the light on fractal geometry and particularly on IFS as a possibly generative model, and we hope that these few examples of experiments demonstrate the potentiality of this model. But we work also on other models, particularly on cellular automata of numerous kinds. What all of these models share, is the notion of form as result of a process. Through these models, our aim is to renew the “sense” of form, space and order within the mind of our students, within their understanding, even maybe within their “perception”, if we admit that even perception may be taught and informed. Fractal geometry should open to them a world of freedom, but not without some rigour, some control over what they do.

References

[1] Ching, Francis D. K., Architecture, Form, Space and Order, Van Nostrand Reinhold

[2] Barnsley, Michael, Fractals everywhere, Acafemic Press, 1988

[3] Eglash, Ron, African Fractals, Rutgers University Press, 1999