Breeding new designs

The use of morphing algorithms in design computation

Dipl. Des. Ole Werner

Department of Product-Design, University of Kassel , Germany.

e-mail: Ole_werner@web.de

Abstract

This paper proposes new ways of using morphing algorithms in design computation. The use of morphing algorithms in design processes is not really new however the intention they are used today. If the method so far was exclusively used in the fields of optimization and engineering design, it has the potential to gain new meanings as a generative form-giving tool.

Morphing is the transformation of a form by the effect of forces. These forces can be naturally arising or freely invented forces. Morphing based optimization procedures usually use naturally arising forces such as air resistance.

The approach described with this paper examines the form manipulation on the basis of invented forces, represented by the geometries of goal forms. The use of goal forms allows the intuitive manipulation of product-designs without sophisticated mathematical knowledge and therefore may attract attention to a large group of designers.

Introduction

Discussing the use of morphing algorithms, probably everyone remembers Michael Jackson's music video "Black and White" directed by John Landis in 1991. Different faces are transformed continuously into others. Nowadays these effects are everyday business in the fields of visual media.

While the mentioned music video only transforms two-dimensional picture sequences, morphing became a standard operation in 3D Animation today. The geometry of a character in position A is transferred into a geometry of the same character in position B. The computer calculates the intermediate positions and creates a smooth movement. In animation morphing is the continuous transformation of a given starting geometry into a given goal geometry. Morphing designates the way between two conditions and thereby describes no end of intermediate conditions.

However computer applications permit not only the change into given goal forms, but allow transformations on the basis of physical rules and regularities today. The animation of clothes or water is a well-known example. The appearance of fabric or water corresponds to naturally arising forces like gravity or wind. The necessary models and algorithms were invented by engineering sciences [1]. The best known example is done research on the construction of bridges. The simulation of naturally arising forces determines the construction of airplanes and ships as well. The shape of an airplane depends on the airflow, it depends on the interaction of internal and external forces [2].

While the effect of these forces had to be examined with the help of complex and time-consuming models in the past, nowadays they can be computed on the base of procedures like Computational Fluid Dynamics and Finite Elements Method. The output of these models is the result of a morphologic evaluation focusing on optimization. However to compute constructions like bridges or airplanes, the functional requirements need to be defined by mathematical expressions. The need of sophisticated mathematical knowledge may be one reason why this method was exclusively used in the fields of optimization and engineering design so far (Figure 01).

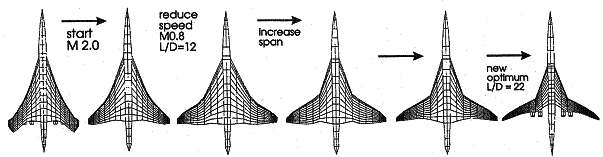
Figure 01: A supersonic aircraft is optimized for the subsonic region, A. van de Velden [3]

If we try to give a general definition at this point, morphing is the transformation of a form by the effect of forces. These forces can be naturally arising or freely invented forces. Morphing based optimization procedures usually use naturally arising while morphing based animation uses both, naturally arising and freely invented forces.

The use of morphing algorithms as a generative tools

As described above, the use of morphing algorithms to optimize various constructions seems to be a common method in the fields of design. But what is going to happen if one shifts the origin intention to gain variety of forms instead of reducing variety to an optimum? What is going to happen if one excludes the optimization for the time and uses morphing algorithms in the way they are used for animations?

The form of a design A is going to be transformed into the form of a design B. Thereby the computer calculates the intermediate geometries and creates a film sequence, which can be stopped at any point. If one stops this sequence before reaching the end, if the dynamic process of the transformation is frozen before reaching the goal form, one receives a design C showing characteristics of design A and design B.

Regarding the biology one can describe this procedure as a generative process: form C is the result of interbreeding shape A with shape B. But C is just one out of infinitely many solutions. Similarities between this process and breeding animals or plants are obvious: Breeding is the goal-directed evolution within one species and creates variations of already existing species. The advantage of this analogy is in fact that one neither need to know how the characteristics of an individual are represented, nor how they pass on. When humans began to domesticate animals and to cultivate plants, they could only observe the results of interbreeding procedures. Only many years later the first theories of genetics arose.

Nevertheless it is briefly to be dealt with the black box of morphing algorithms: Mesh morphing, meaning the continuous transformation of a three-dimensional starting geometry into a three-dimensional goal geometry, is described as a two-stage process. It is differentiated between preprocessing and interpolation. During the first step, the correspondence between the geometries needs to be determined. Therefore they get divided into corresponding surfaces and transferred into the same virtual space. The intermediate geometries get computed during the interpolation. This sounds simple at first, but if one is looking at today's applications most implemented morphing or blending procedures do not obtain acceptable results in all cases (Figure 02). A good morph should be received as a natural and smooth change, the corresponding elements of the starting and target object should turn into each other (nose to nose, ear to ear etc.) and if possible no artifacts or recognizable errors should occur.

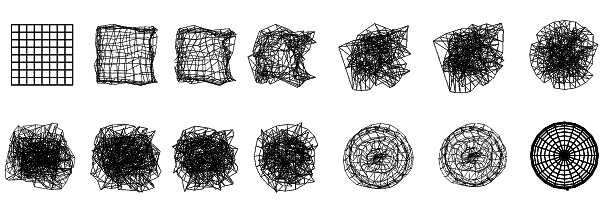Figure 02: Continuous transformation between a cube and a spere (Maya)

According to the two main processes, preprocessing and interpolation, there can be defined two central problems of mesh morphing. The correspondence problem, which point of the starting-geometry corresponds to which point of the target-geometry, and the vertex path problem (interpolation problem), on which way does the point reach its destination.

The actual solutions to solve the correspondence problem can be divided into two groups: The first relies on dismantling the geometries into corresponding and parametrizised surfaces by the user. It allows control of the correspondence information, however it is connected with substantial work and can only badly be supported by the computer. The second solution suggests an automated dismantling and parametrizing of the geometries. But this gives little control to the user and succeeded so far only for certain model classes. Intensive research at the GRIS (Institute for Graphic Interactive Systems) of the technical University Darmstadt is accomplished to improve this second solution. The goal of the research is to expand the automated correspondence identification to a large class of geometries and to improve the users control [4].

The second large challenge is the interpolation. The frequently used naive-linear interpolation may cause intersections and deformations of the geometries. These problems can be avoided by interpolating lengths and angles instead of points [5] or by introducing an additional skeleton [6].

Although the central problems of mesh morphing are solved, yet, a practically working system is not available [7].

Breeding coffee- and teapots

If one remains with the metaphor breeding, the first step is to select a species. In this case coffee- and teapots were selected. Above all this has practical reasons. Only rotated geometries were selected, since their two-dimensional description contains all information necessary to transfer them into the three-dimensional space. There is no difference whether the coffee- and teapots are morphed in two or three-dimensional space. Thus the problem of missing algorithms to morph three-dimensional geometries can be by-passed.

After this, suitable breeding-pots need to be selected in a second step. The Internet offers a huge stock of images that can be used as gene pool. With the help of the search engine Google the Internet is scanned for images referring to the search words "coffee-pot" and "teapot" in order to meet a preselection. This preselection is reduced to thirty images due to further criteria such as symmetry of the body, distinction or quality of the picture. In a third step the selected images need to be converted into vector geometries (outlines). Thereby potential interference factors (background, unequal resolution etc.) can be avoided (Figure 03).

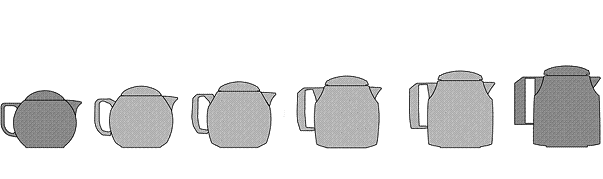
Figure 03 / 04: Transformation into vector geometries / Morhing of complete pots

In the first series of experiments each of the 30 input-geometries is morphed with the 29 remaining. With every morphing process 20 intermediate geometries are computed. Thus altogether 8,700 new geometries or descendants result (Figure 05). In order to create a second and third generation these new geometries become input-geometries themselves in the next series. That means, a selection of the descendants (first / second generation) becomes parents of the second / third generation.

Figure 05: Selected examples, first series of experiments

Briefly regarded, all resulting bodies appear as suitable new coffeepots. In its appearance some of them are quite close to the original objects, while others do surprise. The following can be held: The more strongly the topologies of the input-geometries deviate from each other, the more frequently surprising results arise. And the more closely the topologies correspond with each other, the easier the results can be predicted. Facts that do not surprise particularly, if one consider the basic principles of morphing algorithms. Nevertheless surprising observation can be made. Some resulting shapes are quite close to well-known coffee or teapots, although these have not been part of the morphing process.

The results of the first two series of experiments refer to a special problem: Because every input-geometry is limited on its body outline, most results can hardly be identified as coffee or teapots. Typical characteristics are missing. The results rather suggest associations to vases or urns. For this reason a selection of complete pots (including handle and spout) is morphed in the next series (Figure 04). This series examines the validity of the principle and thus the validity of the two preceding series of experiments.

The solution space of morphing operations

The morphing operation requires at least two input-geometries. They mark the starting point and end of a linear transformation process. Thus in this case the solution space can be described as a straight line, limited by two input geometries. All descendants of this morphing process, as well as all descendants of the subsequent generations, are positioned on the same straight line. In morphing processes this straight line is usually described as time axis. The starting geometry always obtains the value 0 and the goal form always the value 1.

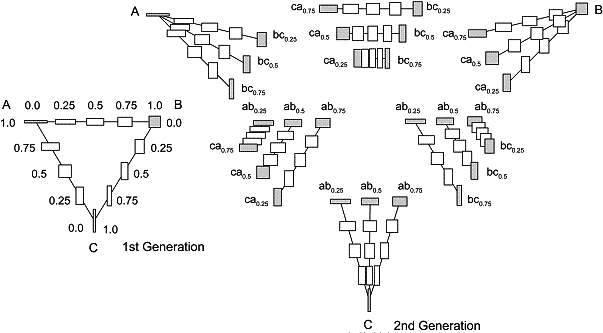
Figure 06: Solution space of morphing operations based on three input-geometries

According to the number of intermediate stages this time axis is then partitioned equally. If a morphing operation creates two intermediate geometries, the axle is divided into three parts. The first intermediate geometry is described by position 1/3 and second by position 2/3. According to this 10 intermediate geometries are described by the positions 1/11, 2/11, 3/11,4/11 etc.

The solution space of morphing operations based on three input-geometries can be described as a triangular area. Straight lines between the three geometries define the two dimensional area. In order to check the validity of this model the second and third generation were examined. Within the triangular solution space morphing operations can be described with the help of straight lines. These lines are running crosswise and intersect at certain points but every intersection describes only one geometry. In order by-pass peculiarities or inaccuracies, caused by the morphing algorithm, only basic geometries were used in this experiment (Figure 06).

According to the preceding examples the solution space, limited by four geometries, can be described as a three dimensional area. And like before, at every intersection only one geometry is described.

Morphing processes can be controlled with the algorithm and the input-geometries. If one takes the algorithm as given and unchangeable only the geometries remain as variable parameters of the process. They become variable parameters of the solution space and each corresponds to one dimension. Therefore the model of the solution space depends on the number of dimensions. According to this, the solution space of the first series of experiments contains 29 dimensions. One out of 30 input geometries becomes the starting-geometry, which can be manipulated with the help of the 29 remaining geometries (parameters). The solution space of morphing operations can be described as n-dimensional space, whereby n is corresponding to the number of variable parameters.

Evaluation of the solution space

The construction of a solution space does not only include increasing variety but also reducing variety. A solution space can be extended or limited by:

1) Adding and excluding input-geometries.

2) Restrictions of the morphing operation (e.g. permitted number of intermediate geometries or the restriction on a defined range of the transformation axle (time axis)).

3) The use of computer-aided procedures to evaluate resulting geometries according to defined criteria. Geometries that do not fullfill the requirements can either be excluded or modified. All criteria used for automated evaluation must be computable (volume, price, weight, technical negotiability).

Figure 07 / 08: Simulated morpging operation (I-DEAS) / Automated evaluation procedure

To compute defined criteria, the morphing process needs to be transferred into computer-aided-design applications. Because the chosen application I-DEAS does not offer morphing operations, they have to be simulated by using the loft operation. The loft operation creates a three-dimensional solid on the basis of two cross sections (outlines of coffee-pots). The two cross sections are transferred into one another by a constant transformation similar to the morphing operation. New cross sections can be extracted and rotated from this solid (Figure 07). The solids, created in this procedure, can be used for computer-aided evaluation. Defined criteria can be misalignment of weight when pouring out, distance between the centre of gravity and handle necessary angle for emptying the pot (Figure 08) or size of the surface in proportion to volume.

Figure 09: Physical models of morphed nature forms

But even if all used geometries of coffee- and teapots are based on physically existing cans, the additional evaluation of physical models (scale 1:1) can be very helpfull. Physical models supply information, which cannot be computed. Surely one can try to evaluate proportions on the basis of computer representations, but with high probability the evaluation of physical models will come to different results. Experiences, gained thereby, can be formalized again and then be implemented into an automated system.

Increasing variety

In the preceding series of experiments the different geometries were always morphed with geometries of the same species, coffee- and teapots with coffee- and teapots. The solution space convinces by the large portion of suitable solutions (without consideration of aesthetic preferences). But at the same time these solutions offer only little surprises or innovations. The borders, determined by the preselection of geometries of only one species, seem to be quite close.

The following two series of experiments shift these borders and expand the solution space by supplementing by new geometries of different species. This is a big advantage of breeding designs on the computer. One is not limited to interbreed within one species, like breeders normally are. Using morphing algorithms one can interbreed every species with every different one.

The first series is using the outlines of the preselected pots, like before and additionally new outlines of glasses, posts and table legs. In the next series the outlines of coffee- and teapots are excluded. Instead of using already designed input-geometries this experiment is based on grown nature forms like leafs, blooms and branches. They are reduced to their outline and rotated along their center axle (Figure 9 / 10).

Figure 10: Selected examples, series of experiments using nature forms

The results can be summarized quite briefly. The less the input-geometries are predetermined by meanings, the more freely the results can be interpreted. In particular the morphs of nature forms offer space for free associations like vase, candle stand, streetlights or wine glasses (Figure 10). This space is only limited by the dominance of the rotation-symmetry. Thus morphing algorithms can also be used as initial-tools during early stages of the design process.

References

[1-2] Böhm, Florian: Evolutionäres Entwerfen? - Florian Böhm im Gespräch mit Sabine Kraft und Schirin Taraz-Beinholt. In: ARCH +, Zeitschrift für Architektur und Städtebau,

Ausgabe 159/60, ARCH + Verlag GmbH, Aachen 05/2002, S. 128-133

[3] ARCH +, Zeitschrift für Architektur und Städtebau, Ausgabe 159/60, ARCH + Verlag GmbH, Aachen 05/2002, S. 128 –133

[4] Alexa, Marc: Morphing von Polyedermodellen, GRIS / GDV Jahresbericht 1999, Technische Universität Darmstadt 1999

[5] Sederberg, T.W.: 2-D shape blending: an intrinsic solution to the vertex path problem Computer Graphics 27, 1993, S. 15-18

[6] Shapira, M.; Rappoport, A.; Shape blending using the starskeleton representation. IEEE CG&A, 1993, S. 44-51

[7] Alexa, Marc: Mesh Morphing - State of The Art Report. Eurographics Association 2001