On the Art of Designing Science

Abstract

Science is sometimes described (or better: mistaken) as the venture of seeking knowledge or the objective truth about things in Nature. Design might not exactly be a science but many of its various sub-disciplines are trying hard to achieve or to maintain scientific status for a number of reasons. One underlying rationale is that natural science represents truth in some way, that rigorous science brings us closer to truth and that pursuing design scientifically helps make designed products more valid. It is the purpose of this paper to provide an illustrated inversion of this rationale. Using cellular automata systems, tools of scientific origin with various applications in art and design, as examples, this paper first examines how scientific theories and methods depend on design, whereas design can exist independent of science. It then proceeds to briefly discuss some recent generalisations of cellular automata dynamics that, in contrast to the argument in the first part of this paper, seem to attribute primary explanatory power about the universe to cellular automata. Expressions of science are designed, and doing so successfully seems to be an art.

1. Introduction: Science, Nature and Design

To develop our understanding of Nature, scientists observe and analyse our environment to devise theories about it largely by means of reduction, simplification, isolation and generalisation. But there is also no question that the sum of reduced descriptions of natural phenomena is unlikely to produce adequate or complete representations of Nature. Art and design traditionally find numerous paradigms and substantial inspiration in Nature. Generative art and design, in a somewhat more formal mode of operation, also apply principles, techniques and models of natural phenomena that have arisen from the scientific field. Examples are genetic algorithms, fractals, neural networks, replacement grammars, and – as the proceedings of the GA conferences demonstrate – cellular automata. There are a number of reasons for applying scientific tools to design. They include the wish to model or mimic phenomena we can observe in Nature by formalised means, the wish to make designing more valid by applying scientific rigour, the wish to produce generalised knowledge about form and design to inform work in design or in other fields and the simple wish for tools that produce form and support the automation of production. The general idea is that some connecting relationship exists between science and design. But what is the nature of this relationship and which of the two fields came first? Design’s ambition to be scientific seems to imply its inferiority to science (see Glanville [10]). Simon ([13], pp. 132-133) states that “the natural sciences are concerned with how things are [while] design, on the other hand, is concerned with how things ought to be, with devising artefacts to attain goals”. In this sense, design can hardly have originated from science whereas design might well have possessed the devices to spawn science. Accordingly, Glanville observes that design is not a subset of science but that science is rather a subset of design. Adopting this perspective, it can be stated that scientific tools and models are design products. The following sections aim at further substantiating this argument by discussing a variety of design features of cellular automata in place of all scientific models.

2. Choices and Constraints in Cellular Automata Design

Existing in and forming part of time and space, we are in a very difficult position to understand space-time, for the simple reason that we cannot step outside of it to compare a universe with time and space to one without, in order to spot the differences. We have a number of theories and models of space-time, but with space and time being not only essential constituents of our physical universe but probably also of ourselves and our perception, it is difficult to conclusively and scientifically prove or disprove one or the other of them. Most theoretical models of space-time differ only at the astronomical scale and perform practically identical at the scale of human experience. Despite our deficient understanding of space-time, theoretical models (or black boxes) of it are used as bases upon which to formulate other, less fundamental model. Involving concepts of space and time, cellular automata are designed to provide tempo-spatial conditions for cellular “evolution”. These conditions are typically modelled to be uniform within the cellular system following scientists who believe that the laws of Nature are uniform in space and time.

Humans experience time and space as continuous phenomena. Movement through space and aging are not perceived as progress through “granular” environments. We nevertheless find it necessary to measure time and space in relative as well as in absolute terms to facilitate for instance our social interaction and technical processes. We do this by applying scales of units to distances and durations. Science therefore considers light-years or milliseconds and computers execute and count machine cycles, whereas humans experience smooth progression. We do not know the causal relationship between physical change and time. Is physical change a phenomenon for which time provides an independently progressing degree of freedom or is time the result of change in the physical universe? Or is the search for a causal relationship between the two fundamentally misguided? We do not know. Still, when we model physical systems in the form of cellular automata, we typically model time in the form of discrete steps in which the cellular rule sets are executed. There are theories assuming granularity in space-time with definitive smallest possible units of distance and of time. But again, being caught inside our physical Universe, it would be very difficult for us humans or any physical measuring apparatus to sense its grain. In cellular automata, time and space are non-continuous, i.e. segmented into discrete units. This also applies to the logic states of individual automata cells, which are members of the family of so-called finite-state automata. There is a definitive number of states a cell can adopt. This is largely inconsistent with the physical Nature we perceive. Everyone who has observed decaying fruit for example will agree that it would be very difficult to identify a finite number of states in this continuous process. If a decaying object is a finite state system, it will very likely still involve a large number of states, occurring at a very small scale. We also do not know the extent of physical space and it is frequently assumed that our Universe is infinite. This attribute is of course impossible to achieve in a human-designed system, even though it is an essential element of the conceptual forerunner of cellular automata. The tape of the Turing Machine was designed to be infinite. There are different speculations that assume our Universe to be finite, to expand continuously, to alternately expand and contract or to have a so-called manifold topology, meaning that a finite cubic segment of space repeats itself infinitely in all dimensions (a “three-dimensional torus”).

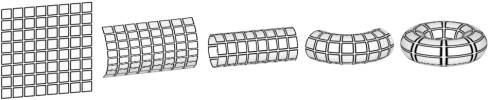
Even though nobody has actually experienced evidence of such a spatial topology in the physical universe yet, this model is frequently used in cellular automata systems to produce infinity-like conditions (i.e. to avoid awkward conditions near the boundaries of a finite grid). Figure 1 shows how a flat two-dimensional automata grid can be transformed into a two-dimensional torus (doughnut) topology. Analogously, higher-dimensional cellular automata systems can be designed to model higher dimensional manifolds’ behaviour if the designer wishes to do so.

Figure 1: Flat torus to 3D torus (“doughnut”) transformation

An automata grid of finite dimension has, in contrast to the physical universe (just as the memory of a von-Neumann computer has in contrast to a Turing Machine) the convenient characteristic of allowing absolute referencing. In programming a Turing-Machine-like system, a great deal of effort is required to enable the program to keep track of “where” it is in relation to given data elements. The programmer of a von-Neumann computer, in contrast, takes the CPU’s external view on memory and can refer to memory elements using absolute addresses. So if a cellular automata system were to exceed close-range cellular neighbouring relations, the host system’s top-down perspective and absolute referencing possibilities (compare figure 3) would provide convenient implementation shortcuts that have little correspondence with Nature.

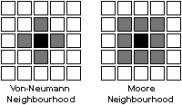
Figure 2: Alternative “neighbourhoods” and cellular automata

In typical cellular automata systems, cells interact (exchange information) with their immediate neighbours only. Usually being arranged in uniform cubic close packing, a configuration that is rather exceptional in Nature, the notion of an immediate neighbour is ambiguous since there are neighbouring cells adjacent to the sides (horizontally, vertically) as well as the vertices (diagonally) of cells. Consequently, there are two typical types of neighbourhoods modelled in cellular automata systems. These are called the “von-Neumann neighbourhood” with four neighbours per cell and the “Moore neighbourhood” with eight neighbours per cell (see figure 2). Neither is inherently correct or wrong. They are designed to suit the requirements of different models, and users are free to choose. Cellular automata systems have been designed that are based on both types of neighbourhoods at the same time, such as a growth structure demonstrated by Schrandt and Ulam (see [9], figure 1). Others have used entirely different models of cellular neighbourhoods.

In cellular tissues in Nature, information exchange between cells can take place in close, middle and long ranges ([6], p. 268 ff.), sometimes requiring rather long stretches of time, sometimes operating extremely quickly, as in electric impulses or crystalline chain reactions. The definition of the cellular neighbourhood is up to the designer of the experiment in which they are implemented. The awkward ambiguity between different types of direct neighbours in cubic tissues can be avoided by designing cellular automata based on hexagonally close-packed structures as shown in figure 8. Cellular automata systems can furthermore be designed to operate using uniform or non-uniform rule sets, uniform or non-uniform cellular geometries, and also to manipulate all these design features dynamically during runtime by various means. These areas haven’t yet been the subjects of extensive investigations. While all these design choices discussed above are quite obvious, less obvious and subtler ones exist.

It is often noted that all parallel processes can be simulated in serial. With most contemporary computing machinery built around one or very few sequentially operating processors, this statement is reassuring to those who whish to emulate parallel physical processes on commonplace digital computers. John Conway’s Game of Life is a classic example. Using cellular automata, simulated on a single CPU, it has been compared with or used to simulate various types of natural dynamic systems such as population dynamics, adaptation, competition and evolution. From a mathematical viewpoint, it might indeed be possible to re-model a parallel algorithm to perform in serial, producing an equivalent end result. One outcome can be based on more than one causal process. In Generative Design, it is however very often a dynamic system’s actual process or the form it produces that we are interested in, and not some kind of end result. We typically use cellular automata models to serve open-ended processes as opposed to close-ended calculations. Since process, processes and results are perceived and interpreted differently by different observers, we must take notice of a parallel process and a serial process as two different things. Moreover, in being most usually modelled on serially operating CPU’s, cellular automata systems show gross shortcomings when they are modelled to represent natural phenomena

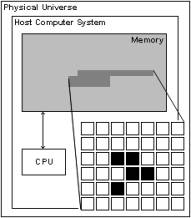
Figure 3: Host CPU operating on CA representation in host memory.

Typical implementations of cellular automata operate (“evolve”) by means of an overall sequential loop that sweeps through the entire system to repeatedly dedicate “time slices” of the hosting CPU to each cell (see figure 3). These time slices are discrete, just as the spatial partition of the cellular grid and the total number of possible cell states are. Slices of host CPU time are dedicated to one single cell at each point in time. After one execution loop is completed and all cells’ transition rules are carried out, another execution loop starts and so forth. The host loop usually scans through the cellular system using one loop structure or multiple nested loops reflecting the number of spatial dimensions of the system (two loops for a two-dimensional system, three loops for a three-dimensional one). As a result, the cellular execution sequence is performed line- or column-wise from top to bottom, from left to right or similarly.

One of the best-known rule sets is that of John Conway’s Game of Life [5]. In this uniform two-dimensional two-state (“alive” and “dead”) system, cells refer to their Moore neighbourhood. The rule set states that living cells with less than 2 or more than 3 alive neighbours die and dead cells with exactly three alive neighbours become alive. As is well known, this rather simple system gives rise to very dynamic and complicated processes, including various local attractor patterns, oscillators and so forth. The so-called glider, discovered by John Conway and shown in Figure 4, is probably the best-known example of a stable but mobile self-reproducing pattern within the system. Its replication capability applies to all four possible rotations of any of its four configurations.

Figure 4: Classic glider replication in John Conway’s “Game of Life”

What is typically not discussed in descriptions of cellular automata systems is the necessity of a secondary data array, acting as a backup buffer behind the scenes. During each execution loop, the state resulting from rule set execution is not assigned to the cell directly but to a separate memory array. Only after the completion of a full execution cycle, the content of this secondary array is mirrored to the primary grid of cells before the next execution cycle commences. This secondary array plays an important role in the dynamics, the stability and especially in the symmetry of behaviours observed in cellular automata systems. The difference it makes lies in the way it suppresses state changes to affect neighbouring cells and their states during the same execution cycle – a capability allowing for immense derivative dynamics to unfold if allowed. Carrying out the rules of the Game of Life without implementing this backup buffer could lead to behaviour such as that illustrated in figure 5 below. The Sequence starts out with a classic glider configuration. However, within the four execution loops expected to be required for a displaced copy of the initial glider configuration to re-emerge, the pattern has evolved into a static “still life” of four cells that is also known as a ”tub”.

Figure 5: Progression from glider pattern in cellular system without backup buffer

Why does the secondary array exist and what does it imply when compared to the physical universe? One might speculate that the original computers hosting early Artificial Life systems were rather slow machines and that an ongoing and immediate effectiveness of state changes during each execution cycle would have visually revealed the jerky line-by-line scanning of the host system. It would have destroyed the Nature-like beauty of the game. The design decision of introducing a secondary backup array as a kind of Z-buffer might have improved the visual quality with instantaneous overall updates. But the way in which it has been implemented has a significant influence on the system’s logic that undermines its resemblance to natural physics. Cellular automata are often associated with autonomous “objects” or “agents” whose collective decentralised action develops emergent properties. Cells in the Game of Life and most other cellular automata do however not comply with this interpretation since, as described here, their performance is not independent of centralised and synchronised control. Elements of physical systems show response to changes in conditions immediately or maybe with some delay, but (at least according to our perception of the physical universe) they do not wait for a universal backup buffer to be written for all types of particles and then for the buffer to be mirrored back into the primary representation of physical reality.

Another reason for the introduction of the backup buffer might have been that without it, processes unfolding in cellular automata systems are largely dependent on the order of cellular execution: of the sequence in which the host system visits individual cells to perform their transitional programs. Different results would be achieved depending on whether horizontal scans are given preference over vertical scans or vice versa, or if cells are executed in a random sequence. In this sense, the progression shown in Figure 5 can only be observed in a system that scans left-to-right lines from the top to the bottom. Other scanning sequences would produce different results than the one shown in figure 5. If desired, increasing the quantity of information in the system can compensate this effect. Figure 6 shows how a six-state system can be designed to produce stable Game-of-Life-like behaviour without backup buffer despite random cellular execution order, by introducing additional transitional cycles.

Figure 6: Six-state glider replication in random execution sequence without backup buffer

Synchronicity is a key property of most cellular automata systems. Without it, cellular automata are very difficult to program and control to produce desired results. But with synchronicity being the result and side effect of sequential simulation of parallel processes, the importance of this design feature often goes unnoticed. Where parallel automata are not simulated but in fact implemented in discrete hardware units, ingenious tricks are required to synchronise execution. Frazer, for example, presents a hardware design by Quijano and Rastogi (see Frazer [4], p. 56) in which an array of physical automata is fitted with a light sensor and synchronised by a strobe light. To allow manageable operation, all cells in a system should be executed equally often and no cell should be executed twice before all other cells are executed once (figure 3 fulfils this criterion). This means than within each execution loop, cells can be scanned and executed spatially as shown on top of figure 7. As mentioned above, one disadvantage of this approach is that without a global backup buffer, it can reveal the un-natural-looking scanning behaviour of the system. Alternatively, cells could be executed in a random sequence within every overall loop. A disadvantage is, however, that during multiple execution loops, certain individual cells are likely to be executed twice before others are executed once. The illustration in the middle of figure 7 shows how cells E and F are executed twice while cell D is omitted by the random sequence. In experimenting with morphogenetic automata systems applications [3] that start cellular development from initial zygote cells to proliferate into void space, I found it useful to use the age of cells as a sequencing criterion as illustrated at the bottom of figure 7.

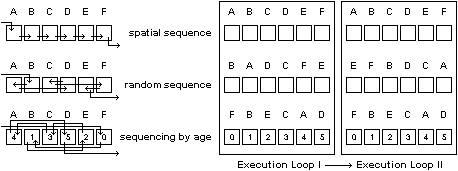
Figure 7: Some alternative strategies in loop sequencing

It seems obvious that the cellular phenomena we observe in Nature manage to produce far richer developments than man-made cellular automata do, without having to pay much attention to the above considerations. Consequently, alternatives to cellular automata have been proposed that are said to model natural processes more realistically in a number of ways [14]. For instance natural cellular systems are richer than many cellular automata systems in that they manage to break symmetry and to express local differentiations. In this sense, the synchronised backup buffer used in the Game of Life and in Schrandt and Ulam’s growth system seems to present a strong limitation, since in these systems symmetric initial configurations can only continue to develop symmetrically. Breaking synchronicity makes it easy to break symmetry. Alan Turing [15] was among the first who have examined symmetry-breaking capabilities in morphogenetic processes. His reaction diffusion model describes how initially symmetric systems can develop into asymmetric configurations and how initially homogenous systems can express local attributes such as limbs and organs. It describes how small-scale effects such as thermal or Brownian motion or cell-internal asymmetry can give rise to asymmetric pattern differentiation. Biologists have observed a yet simpler strategy for expressing local differences in tissues in the eye disk development of the fruit fly drosophila melanogaster (this model is discussed in [6] and a cellular automata model of it was discussed in [2]). The model describes the expression of hexagonal ommatidia with 20 cells of seven types from a hexagonally close-packed two-dimensional array of equal cells. A signalling wave (shown in black in figure 8) sweeps across the eye disk, triggering a state change in which cells behind the wave try to ‘lock’ surrounding cells to form two rings around themselves, consisting of cells that have not managed to lock such two rings. To mimic this behaviour, a cellular automata system can be programmed in different ways, including one approach in which no propagating signalling wave is required when the sequential scanning direction in a procedurally simulated system is exploited to perform its function.

Figure 8: Model of pattern expression in eye disk development during Drosophila Melanogaster embryogenesis

Once local attributes such as organs are expressed, further questions arise with respect to system orchestration that can be answered by various alternative design decisions. Figure 9 shows a Game of Life system with an expressed organ consisting of nine cells. The lower-level cellular process (glider progression) determines the state of the higher-level organ – in this case the organ state is 1 when more than two cells “become alive” and 0 when less than three cells are “alive”.

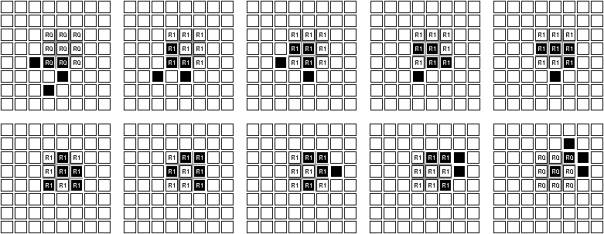
Figure 9: Glider traversing organ

Higher-level cellular automata with features such as organ expression and interaction on higher levels than that of cellular interaction remain comparatively rare (for a recent example see [8]). One reason for this might be that systems of this kind involve some difficult design questions especially with respect to timing and synchronisation matters. How are host time slices to be assigned to elements on the system? Does the action of an organ require dedicated higher-level rules and processing or should it be a mere side effect of low-level cellular activity? The action of discrete elements in von Neumann’s Universal Constructor (construction arm, construction unit, tape unit etc.) are the result of low-level cellular activity only. Alternatively, the illustration in figure 9 was produced with an additional explicit organ rule set that was executed separately at the end of every execution loop. Again, it is questionable to what extent these strategies simulate actual behaviour of hierarchical higher-level processes in natural higher organisms. It seems difficult to grasp the dynamics of hierarchical systems with ever-smaller elements and the temporal causalities their interactions produce. It has been suggested that the common model of a globally synchronous linear time might be an inappropriate starting point for investigation into problems of this kind, and it has even been proposed that it might be fundamentally false. Recently, scientists have suggested that hierarchical organic processes might not only be fractally organised, but that they might be a consequence of a fractal nature of space-time [10][12].

3. Evolution Towards Better Models

The “design quality” of scientific tools such as theories and models depends on how reliable and helpful they are to their users. Cellular automata actually have attributes that strikingly resemble some aspects of natural particle interaction, going beyond the original purposes they were modelled for. This has without doubt strengthened belief in their scientific significance. The fact that there are patterns of cellular automata states that can only exist as initial states and cannot be the result of cellular evolution (so-called garden-of-eden configurations) for example is in some ways redolent of the phenomenon of thermodynamic irreversibility.

Once some observed natural phenomena have been reduced to form a scientific model, it is important that this model in turn be proven effective in making statements or predictions about Nature. For instance, one might attempt to use cellular evolution to predict thermodynamic processes in order to test the usefulness of cellular automata as models. Our observations of physical reality inform science so that science can generalise them to inform our interpretation of other observations we make from physical reality. What is particularly startling about typical cellular automata in this context is that they, being a scientific model, are almost as confusing as Natural phenomena themselves. But as a tool for “chaos science” that is exactly one of the key the points. It demonstrates how complicated natural phenomena with unknown underlying rules and cellular automata evolution with known simple rules can look very similar, as was already stated very early on in cellular automata research (see Schrandt and Ulam, pp. 219 ff. in Burks [1]). Another early point was to show that life and self-reproduction are based on logic processes that can be imitated using appropriately designed simple techniques. However, neither of these points can effectively support the reverse argument, which is to state that therefore everything in Nature is necessarily based on very simple processes. Recently, in the field of cellular automata research, the observation that simple rules can give rise to complicated patterns has been generalised into a New Kind of Science [17] concluding that more or less everything in the physical universe is based on simple rules. In the majority of Wolfram’s models, “simple rules” refer to binary signals that are exchanged in immediate neighbourhoods of one-dimensional globally synchronised two-state automata with Boolean rule sets. Another vaguely explicit generalisation of observations made in cellular automata published in the same work states that the physical universe can be modelled using cellular automata, that specific instances of cellular automata can be described as computationally universal and that therefore the universe must be computationally universal. The value of these theories and the mechanistic assumptions upon which they are built remain to be proven but it seems that they do not significantly enlighten our understanding of Nature. Nor do they allow the formulation of any statements or predictions about phenomena in Nature. Consequently, the author suggests that the practitioner of his science “just watch and see” the Universe unfold ([17], p. 846).

Regardless oversimplified theories, it must be acknowledged that simple rules giving rise to complicated emergent behaviour do not represent the only type of potentially interesting composite dynamic systems. Simple phenomena can also give rise to simple overall properties and complex phenomena can give rise to complex as well as to simple overall properties. Moreover, systems of all these kinds can occur in arbitrary combinations, configurations and quantities. Hierarchical parallelism in particular seems to bear some key secrets of natural phenomena such as life and space-time. At the same time, it poses a major challenge for dynamic systems modelling and the limitations of procedural digital computation could turn out to be a key obstacle in unlocking these secrets.

In the natural universe, we mostly observe systems with multiple, non-uniform elements. These are neither synchronised, nor fixed in grids. They co-exist at equal scales with similar physical dimensions or nested in different scales of granularity and they seem to have large numbers of states. The relationship between simple rules and large numbers of states seems to be closely related to questions of relative scale. Observations in higher-level systems substantiate this assumption. There are very few general scientific theories to investigate these issues. One theory is Koestler’s [11] holon theory which defines a ‘holon’ as a stable, quasi-autonomous whole or a part of a hierarchical system. Holons exist in parallel at the same and at different levels of scale, and combine to form other holons within a self-organising hierarchy. Genes, cells, organs and organisms are typical examples, all showing relative independence from the structure of which they are part, while still being ultimately controlled by it to some extent. Scientists are only beginning to develop models embracing principles of this kind. The result might be scientifically more useful than cellular automata models, but it will again most likely be man-made, incomplete and a makeshift solution.

4. Conclusion

Even though we use them to represent Nature, scientific models are man-made and incomplete. They are devised for specific purposes and in specific contexts and are the result of ultimately pragmatic design decisions and design constraints. Existing scientific models could have been designed in different ways and many of them will be modified to meet changing requirements in the future. We use cellular automata and other scientific models to drive design for various reasons. Before adopting them too swiftly in order to substantiate other man-made designs ‘scientifically’, or even to devise new sciences based on them, we need to understand that models of this kind have been the result of design in the first place. The resemblance of some phenomena in cellular automata with natural phenomena can hardly legitimise the general reverse deduction that the universe resembles cellular automata.

5. Acknowledgements

I gratefully acknowledge the support and inspiration from my colleagues at the Spatial Information Architecture Lab at the Royal Melbourne Institute of Technology and at the School of Design at The Hong Kong Polytechnic University, in particular Timothy Jachna.

6. References

[1] Burks, Arthur W., ed. (1970): Essays on Cellular Automata. University of Illinois Press, Urbana, Chicago and London.

[2] Fischer, Thomas, Fischer, Torben and Ceccato, Cristiano (2002): Distributed Agents for Morphologic and Behavioral Expression in Cellular Design Systems. In: Proctor, George (ed.): Thresholds. Proceedings of the 2002 Conference of the Association for Computer Aided Design in Architecture. Department of Architecture, College of Environmental Design, California State Polytechnic University, Pomona, Los Angeles, pp. 113-123.

[3] Fischer, Thomas (2002): Computation-Universal Voxel Automata as Material for Generative Design Education. In: Soddu, Celestino (ed.): The Proceedings of the 5th Conference and Exhibition on Generative Art 2002. Generative Design Lab, DiAP, Politechnico di Milano University, Italy, pp. 10.1-10.11.

[4] Frazer, John H. (1995): An Evolutionary Architecture. Architectural Association. London.

[5] Gardner, Martin (1970): Mathematical Games. The Fantastic Combinations of John Conway's New Solitaire Game "Life". Scientific American 223, October 1970, pp. 120-123.

[6] Gerhart, J. and Kirschner M. (1997). Cells, Embryos, and Evolution. Toward a Cellular and Developmental Understanding of Phenotypic Variation and Evolutionary Adaptability. Malden, MA: Blackwell Science.

[7] Glanville, Ranulph (1999): Researching Design and Design Research. In: Design Issues. Vol 15, No. 2, Summer 1999, pp. 80-91.

[8] Helvik, Torbjørn and Baas, Nils A. (2002): Higher Order Cellular Automata. Poster presented at the Workshop on Dynamics of Biological Systems, Krogerup Højskole, Denmark. URL: http://www.math.ntnu.no/~torbjohe/pub/HOCAposter.pdf [Nov. 2003].

[9] Herr, Christiane M. (2003): Using Cellular Automata to Challenge Cookie-Cutter Architecture. In: Soddu, C. (ed.): The Proceedings of the 5th Conference on Generative Art 2003. Generative Design Lab, DiAP, Politechnico di Milano University, Italy, pp. xx-xx

[10] Ho, Mae-Wan (1997): The New Age of the Organism. In: Jencks, Charles (ed.): Architectural Design Profile No. 129, New Science New Architecture, pp. 44-51.

[11] Koestler, Artur (1967): The Ghost in the Machine. Cambridge University Press, Cambridge, UK.

[12] Nottale, Laurent (1996): Scale Relativity an d Fractal Space-Time: Applications to Quantum Physics, Cosmology and Chaotic Systems. Chaos, Solitons and Fractals 7, pp. 877-938.

[13] Simon, Herbert A. (1969): The Sciences of the Artificial. MIT Press, Cambridge, Massachusetts.

[14] Stark, Richard W. and Hughes, William H. (2000): Asynchronous, Irregular Automata Nets: The Path not Taken. In: BioSystems, No. 55, pp. 107-117.

[15] Turing, Alan M.: (1952): The Chemical Basis of Morphogenesis. In: Phil. Trans. R. Soc. London B, 237. pp. 37-72.

[16] Weeks, Jeffrey R. (2002): The Shape of Space. Second Edition. Marcel Dekker Inc., New York and Basel.

[17] Wolfram, S. (2002): A New Kind of Science. Wolfram Media, Champaign, IL.