Selectionist musical automata

Integrating explicit instruction and evolutionary algorithms

Peter Beyls

peter.beyls@pandora.be

Abstract

We describe an open, modular system for experimentation with algorithmic composition. It integrates evolutionary methods for implicit synthesis of complex hierarchical structures as well as a large library of software tools allowing user directed explicit object manipulation. The idea is to combine the generative potential of genetic methods with the instructive power of user control embedded in knowledge and culture. Melodic material is generated by viewing the rewrite rules of both L-systems and linear cellular automata as genotypes. The user creates cross-overs and mutations according to visual/auditory interactive evaluation. One can traverse genetic space by morphing one rule into another. Further, objects are visualised in a graphic interface and available for direct manipulation, analysis and structural assembly. A complex harmonisation module creates articulated chords to a given melody based on tension profiles and conventional pattern matching. An embedded interpreter allows the user to extend the functionality of the system which is fully operational and implemented in Object Lisp.

1. Introduction

Much recent work in algorithmic composition and interactive composing has turned to biologically inspired models for the synthesis of coherent yet unpredictable output. The design of programs with true creative impact no longer relies on explicit rules based on a known aesthetic tradition. In contrast, we speculate on the potential of genetic engineering for the synthesis of original musical constructs.

Composition becomes navigation in a virtually infinite search space inhabited by families of related musical objects. Large groups of genotypes are generated at random. A given fitness is attributed through interactive evaluation, and the DNA of a few selected objects is mixed using cross-over and mutation operators. Results may be stored to disk and sorted according a number of critical features. At a later stage, the composer can issue search commands over this database as well as embark on a new exploration from an earlier point of reference.

The process of gradual optimisation allows the composer to control intricate structures without necessarily understanding their underlying complexity. In addition, genetic algorithms provide a way to discover interesting structures that were not anticipated by the composer. Note that the human interactor actually samples a virtually infinite, non-linear search space. The composer conditions the system to favour interesting emergent functionality -- highly in contrast with compositional theories based on explicit structural design.We have applied the evolutive method in three implementations: a program that grows brains for interactive composing; real-time sensor-activator networks with evolved connectivity [Beyls 99, 00], a system which views the rewrite rules of L-systems (Lindenmayer Systems) as genotypes, implemented as Lisp functions of arbitrary nesting complexity and finally, cellular automata with evolved lookup tables. The present paper reports exclusively on the latter two.

However, it is understood that automation by itself seldom yields a complete musical composition. When considering larger musical movements, we often think in terms of development of germinal ideas, of shifting tendencies in time and the critical control of tension profiles i.e. compositions consisting of statements built according to a specific plan. Our system provides a desktop model to handle a pool of musical fragments visualised as boxes freely configured in a workspace. A box contains a figure of arbitrary complexity; a few notes to a complete musical gesture. Typically, melodies are generated from cellular automata or L-systems and imported into the current workspace for further treatment, analysis and assembly.

Our system also allows for genetic interpolation from the specification of two points in genetic space; the result is a shifting musical climate between two points of reference. In addition, we use a novel harmonisation algorithm based on a measure of psychological tension in the melody/chord relationship. Also, our musical workbench provides a large toolbox of functions to edit and transform generated musical material.

In summary, exploration and discovery are implicit to the current approach though the overall intention is the synthesis of scores for human performance, i.e. the system must incorporate knowledge of physical musical instruments.

2. Implementation

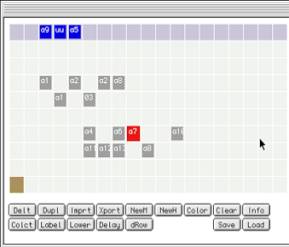
The main interface contains a family of musical objects under observation, visualised as an array of coloured and labelled boxes. One of them is selected and subject to manipulation by the user. The top row is thought of as an assembly line; the user collects boxes into a sequence which can be retrieved into a single, new macro object. The events that constitute the top row are shown in the upper right pane in piano roll notation, the lower pane shows the currently selected object. Figure 1a. Main interface, typical workspace configuration

Any workspace can be saved to disk and later retrieved, like a dynamic sketchbook for musical experimentation -- any interface in the present system provides tools to save and load objects. In addition, the interface provides access to a large set of operators, some of them quite exotic; operators include contrast-expansion, counter melodies according to user-specified intervals, simple rule-based multi timbral orchestration, a conditional filter, the generation of new objects from interpolating between two existing ones, chord generation by a ring modulator inspired function and many more.

The new object which results from a transformation can be appended, prepended or replace the current object. Operators feature appropriate default arguments as well as function-specific program suggested parameters. Since the system aims to be open and modular, we provide an imbedded interpreter where the user may write small Lisp programs and save them into a private library.

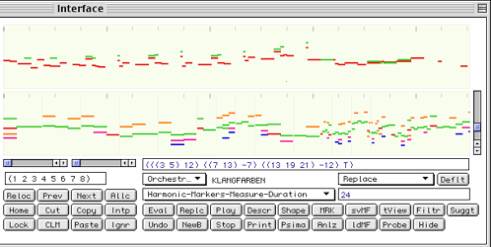
Figure 1b. Main interface, score visualisation

In view of harmonisation, the current melody is subject to segmentation according to 4 potential criteria:

- segmentation according to an explicit grouping parameter list

- segmentation by comparing melody durations to a user specified duration argument, create mark when the event-start-time modulo duration argument equals zero

- segmentation by scanning the melody for user-specified cadences

- segmentation according to values or intervals in melodic tension.

Tension plays an important role when considering the complexity of melodic material. Formally, we use a logarithmic scale [Jaxitron, 85] to compute harmonic tension: a minor-seventh contributes 1, major-second adds 10, major-seventh adds 100 and a minor-second adds 1000, all other intervals add zero. So a melody can be scanned with a certain window, say 5 wide, the local tension sums are collected in a list and subject to inspection. Information on how tension evolves in time is often taken into consideration in the harmonisation module; it may be used as a parameter to control automatic segmentation of melodies.

3. Melody generation by cellular automata

Cellular automata are discrete models of complex dynamical systems [Wolfram, 94]. We implement one dimensional linear automata and think of the rewrite rule as a genotype. Fig. 3 show nine automata with numeric fields for local parameters; lambda parameter in percent, noise value, nr of generations (up to 80), neighbourhood (3, 5 or 7) and nr of values (2 to 8). A CA grows from editable initial conditions. The complexity of a CA is said to belong to one of 4 families; CA evolving to a steady state (point attractor), CA moving into a cycle attractor, CA showing multiple types of relative periodicity and finally, CA featuring strange attractors. A clever tuneable complexity navigator, known as the lambda parameter, was suggested by [Langton, 86]. Basically, it specifies the density of positive values relative to zeroes in the rewrite rule i.e. how many values map to live cells. Thus, it offers a statistic measure of how active the automaton will be.

Visual inspection provides a first hint to the musical potential of a CA. Two automata are selected by mouse pointing to become the parents of a reproductive process; their lookup tables are applied to a cross-over operator and some percentage mutation; from here 9 new children are bred from these 2 parents. The lower pane informs about the current mapping; a melody follows from an elaborate mapping algorithm which uses a mapping neighbourhood of 2, 3, 4, 6 or 12 -- values applicable in a CA with 12 cells wide.

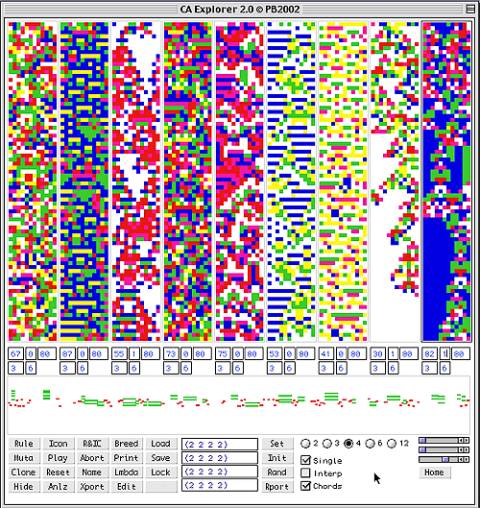
Figure 3. CA main interface.

CA genotypes may be cloned yielding identical structures yet a minimal amount of noise may be used to disturb the functioning of the CA; it may stimulate local structures in an otherwise stable automaton. In addition nearly identical CA can grow from the same rule with minor mutation. Genetic interpolation speaks to the imagination: what if we think of two rules as two points in a huge search space; these two points thought of as anchors of a clear and specific musical climate. So interpolating between the anchors in a few generations yields a trajectory and a potentially characteristic momentum. Any rule is accessible for analysis or explicit editing by the user when hitting the Edit button, in particular if we wish to study the implications of certain values in a rule.

It should be noted that while the combinatorial complexity of genotypes formulated as lookup tables is huge, it is also intrinsically limited. The nature of the rules does not evolve, so the system cannot move into regions of higher hierarchical complexity -- the genetic algorithm does not change the structure of the genotype. L-systems, described in the next paragraph, address this consideration.

4. Melody generation by L-systems

L-systems [Lindenmayer, 68] are prime examples of database amplification systems; a large structure is generated from a simple list of start-tokens and a rewrite rule that is applied recursively for a number of generations. L-systems are similar to type 2 (context free) grammars, they provide a computationally inexpensive way to represent complex patterns showing various degrees of self-similarity and developmental structure. For a formal description of grammars and L-systems in music, see [McCormack].

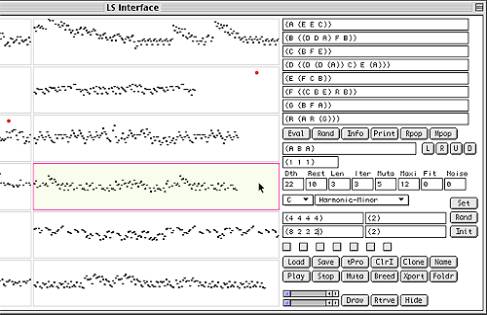
Figure 4. Snapshot of L-system interface.

The genotypes here are not lists but tree structures; cross-over is thought of as replacing local branches at some depth with other branches taken at some other depth from another tree. We have a vocabulary of 8 potential start-tokens; A to G (implies activity) and R (is mapped to a rest). The following editable parameters determine the nature of a rewrite rule:

- Depth: A recursive algorithm is used to compute a new rule; any branch in the nested Lisp structure may feed on itself and spawn additional branches at any given depth. The Depth parameter sets the chance, at any point in the tree, whether branching continues or aborts. Care is taken to avoid infinite feedback -- exit is forced at some given maximum depth. A typical rule is shown in the upper right corner of figure 4.

- Rest: the chance that the R-token is selected over an active token. This is similar to the lambda parameter used to determine the density of activity in cellular automata.

- Len: the maximum length of a rule-part.

- Iter: the number of iterations the rule is applied to the start-tokens.

- Muta: the mutation percentage.

- Maxi: used with the mapping algorithm; it specifies the maximum interval step in the resulting melody.

- Fit: the fitness attributed to the currently selected rule.

- Noise: the amplitude of a noise source set to interfere with the rule.

The start-tokens (‘A B A’ in the current example) are user editable; note that symmetric start-tokens will add coherence to the output, it is one way to balance novelty and unpredictability in the essentially self-contained automaton.

The genotype tree structures are metabolised into polyphonic MIDI patterns and organised into larger musical gestures -- additional interface elements apply to the mapping algorithm: the choice of a tonality, a scheme to select durations at 4 different depths in the resulting tree and a set of check boxes used to inhibit the use of tokens A to G.

The list containing ‘(1 1 1)’ specifies the intervals that will be used to compute melodies. Both the depth of a leaf and its content (A to G) is taken into consideration to compute a new pitch, the depth contributes an additional offset taken from that list (modulo the length of the list). The user proceeds by selecting two phenotypes from critical evaluation; visual inspection and/or by listening to the object. The cross-over operator mixes branches from both parent trees and applies some mutation in order to keep a certain degree of novelty i.e. to keep the system from evolving to a point attractor.

So here again, the system accommodates both generative processes and direct control by a human interactor. A delicate balance is maintained between implicit automation and explicit control. As an example, let’s have a closer, systematic look at a typically hand-crafted mapping algorithm. The L-system generates a tree containing the symbol of every leaf plus its depth. Each symbol is converted into a numeric pointer, pointers are collected in a linear list. Formally, a pointer equals:

(defun transpose-token (symbol interval)

(if (not (eq ‘R token)) ;; skip rest

(+ (nth (position token ‘(A B C D E F G)) interval)

token)))

The list of pointers becomes:

(defmethod compute-pointers ((self lso))

; outputs pointers for pointing in scale plus respective depth

; (starting from 0)

(collect-grammar self)

(loop with ic = 0

with grammar = (grammar-output self)

with d0 = (get-depth-zero grammar)

with d1 = (get-depth-span grammar)

initially (progn (format t "~%Zero depth is ~a and depth span is ~a." d0 d1) (format t "~%Sequence = depth, symbol"))

for tok in (mapcar 'car grammar)

for dth in (mapcar 'second grammar)

when (atom tok)

collect (list (- dth d0)

(transpose-token tok

(* (nth ic (intervals self)) (- dth d0))))

when (and (not (unpack-flag self)) (listp tok))

collect (list (- dth d0)

(loop for e1 in tok collect

(transpose-token e1

(* (nth ic (intervals self))

(- dth d0)))))

when (and (unpack-flag self) (listp tok))

append (loop for e1 in tok collect

(list (- dth d0)

(transpose-token e1

(* (nth ic (intervals self)) (- dth d0)))))

do (setq ic (mod (+ 1 ic) (length (intervals self))))))

The lowest depth value is not necessarily zero, so all depth values are transposed as to have the lowest depth at level 0, the depth span is used to determine pitches. If the unpack-flag is true, the tree is parsed up to the level of a leaf, otherwise the deepest list is considered the top of the tree -- the list is then interpreted as a parallel structure (later to be used as a chord). The algorithm cycles though the intervals. At this point, the resulting list yields a numeric interpretation of the tree, the next step is to provide musical meaning.

A 10 octave scale is created from an explicit selection of both key and mode from popup menus. In addition the user may edit the intervalic structure of any mode; it forms the basis of custom tonality design. The score events are computed as follows,

;; select a duration list from 4 potential ones, according to depth

(setq dur-list (nth (mod depth 4) (durations self)))

;; select a duration value by cycling through every list

(setq dur-value (nth (nth (mod depth 4)

(duration-counters self)) dur-list))

;; a single MIDI event becomes

(when (and (numberp e)

(plusp dur-value) ;; not a rest

(not (nth (mod e 7) (inhibition-flags self)))) ;; token not inhibited

collect (list start-time

;; compute MIDI key number

(if (chroma-flag self) ;; chromatic or diatonic use of depth

(+ bias (* 1 depth) (nth e (scale self))) ;; bias = register of LSO

(+ bias (nth (+ e depth) (scale self))))

dur-value

(if (zerop (nth (mod depth 4) (duration-counters self)))

(+ 90 (random 30)) ;; articulate velocity

(+ 60 (random 20)))

1) ;; channel 1

5. Harmonisation

The harmoniser imports a segmented melody and finds appropriate chords according to constraints specified by the user, it does not incorporate genetic ideas. The central constraint is minimum and maximum harmonic tension between segment and chord, 36 tonalities provide a pool of 432 harmonic alternatives. Harmonisation is viewed as a problem of constraint satisfaction; tension, intended root tone motion, required intersection count of melody and harmony, specific tonalities .. all contribute to the nature of the harmonic path.

An orchestration module is under construction, the goal is to output scores for human performers. An object-oriented database was created documenting the characteristics of acoustic instruments; this information is used to filter musical objects according to constraints in the database. Orchestration includes first, the critical distribution of polyphonic material over a number of instruments according to criteria that may shift in time and, second, the rule-based articulation of melodies assigned to particular instruments that may as well evolve during the life span of a given musical gesture. After some experimentation with a genetic approach (viewing orchestration as an array filled according to genetically derived functions) we adopted a text oriented interface; the user issues Lisp macros to orchestrate the current object. Direct functional expression was felt to be repeatable, reliable as well as flexible. By the way, we may in fact consider textual code as genotype, the approach was applied successfully in the pioneering work of Karl Sims [Sims, 91].

The pragmatic automata described here imply extensive selectionist user interaction; fit objects are selected for breeding new generations. This determines both the strength and weakness of the system; the user navigates a wealthy field of possibilities but that field is highly non-linear and it is very time consuming to evaluate all possibilities at every step in this selective process. So ways to automate selection -- given explicit complexity criteria -- would lower the pressure on the user. We have implemented functions to analyse the time-dependent complexity of CA in terms of periodicity, speed of change in (and acceleration of) periodicity, density in time, evolution of complexity measured using a Hamming window... The idea, then, is to adopt an unsupervised method: generate families of genotypes, evaluate the metabolism which follows and save the result to disk. The user could then explore that database with thousands of objects and issue sort commands -- structures would then be directly accessible given intended characteristics.

6. Conclusion

The methods described aim the combination of exploration and exploitation in a computational environment which stimulates creative decision making -- optimisation in selectionist automata mirrors the creative process of searching through the composers personal search space. Exploitation concentrates on the effective use of a certain momentary niches while exploration means moving on to potentially better, yet unexplored points in combinatorial space. Exploration is analogous to self-confirmation in the creative process while exploration is more like self-revision and seems closer to the heart of true human creativity. Gradual optimisation is extended through explicit stylistic input from a human interactor. The idea is to start from randomness and to grow a pool of related objects -- a field of reference is thus created; goals are identified in a gradual fashion. The user provides constraints, interferes with the functioning of the system by providing initial conditions and tuning parameters and thus complements the otherwise automatic, generative behaviour of the global system. Obviously, this type of intimate machine interaction yields results that could not be produced in isolation by neither man nor machine.

7. References

[Beyls 97] Aesthetic navigation: musical complexity engineering using genetic algorithms, Proceedings of the JIM97, Lyon, France 1997

[Beyls 99] Evolutionary strategies for spontaneous man-machine interaction, Proceedings of the International Computer Music Conference, Beijng, China 1999

[Beyls 00] Synthetic creatures in context, Proceedings of Intersens, Marseilles, France 2000

www.labo-mim.org/pdf intersens/Beyls.pdf

[Jaxitron, 85] Cybernetic Music, Tab Books Inc. 1985

[Langton, 86] Studying artificial life with cellular automata, Physica 2D, Elsevier Science Publishers 1986

[Lindenmayer, 68] Mathematical models of cellular interaction in development, Journal of theoretical biology 18, 1968

[McCormack] Grammar Based Music Composition

www.csse.monash.edu.au/~jonmc/ resources/L-systemsMusic.pdf

[Sims, 91] Artificial evolution for computer graphics, Computer Graphics, Vol.25, Nr. 4, 1991

[Wolfram, 84] Cellular automata and complexity, Collected papers, Addison-Wesley Publishing Co. 1994