Exploring the Massing of Growth in Cellular Automata

Robert J. Krawczyk

College of Architecture, Illinois Institute of Technology, Chicago, IL, USA.

e-mail: krawczyk@iit.edu

Abstract

In the investigation of cellular automata as an architectural massing generator, as a cell survives generations after generation, a question occurred if the survival property could be integrated into the final form so its history is not lost. One method that could be considered is color, single generation cells having a different color than ones surviving multiple generations. Another method is to increase the size of the cell as it survives over time. When both methods are considered they are able to add an interesting variety to the massing of an architecture that is basically made from the regular placement of single cells.

1. Introduction

Cellular automata is a computational method which can simulate the process of growth by describing a complex system by simple individuals following simple rules. An early example of three-dimensional cellular automata was the wooden block model created by Schrandt and Ulam [1]. Bays [2] further developed three-dimensional patterns, as did, Coates [3] for architectural applications, much in the same spirit as Bays. More recent investigation includes two methods developed by Wolfram [4], in which a stacking method is explored, as well as, one similar to Bays. Examples of all of these can be seen in Krawczyk [5]. The striking similarity in all of these is the explicit representation of the cellular automata, even though each had taken a different approach and had a different application as an investigative goal.

In a previous investigation, Krawczyk [5], the primary organizing element, the location of the cell, was interpreted in a variety of architectural elements. Concepts that were demonstrated included: horizontal and vertical connectivity, support structures, floor planes, envelope, and site boundaries. The rules and neighbour configurations were held constant and there was no attempt to research the variety of forms possible when these are considered.

One of the observations from this previous research was that the massing of the cells at any one time never included consideration for the cells that had survived from generation to generation. The question that resulted was: could this property be displayed in some fashion in the final form. Showing this property would increase the visibility of the underlying cellular automata method used. This current research addresses this question.

2. Recording Survival

The first method in recording survival was to simply display the surviving cells in another color. Figures 1a., b., and c. display three original results without color differentiation. Figures 1d., e., and f. display surviving cells in a different color.

a. b. c.

d. e. f.

g. h. i.

Figure 1. Survival as color and shape

The architectural patterns that were generated were interesting but the overall massing still remained the same. The next option was to represent the surviving cells in a different shape from the others. Figures 1g., h., and i. display one such variation, an octagon as the cell shape. These did further accentuate the surviving cells, but were not strongly integrated into the remaining square cells. The horizontal connections were much stronger than the vertical. These results lead to the concept of varying the cells not by shape but by size. Figures 2a., b., and c. display the same results with the surviving cells modified by only height. As the cell survives from generation to generation it increases its height by a small amount. This also enables survival to be represented as growth. Figures 2d., e., and f. display the same results by giving the cells only horizontal growth instead of vertical. Finally, Figures 2g., h., and i. display the results when both horizontal growth is included with growth in height. With growth in all directions, the architectural massing greatly deviates from the regular cellular one of simple square cells. This offers a variety of expression and also a visible history of the survival of cells.

a. b. c.

d. e. f.

g. h. i.

Figure 2. Survival as variation in size

A further investigation could include the rate of increase for each generation or the grouping of cells having survived the same number of generations, color-coded in some fashion. The original shape of the cells could also be varied. This research only considered the square and later the circle as possible plan layouts.

2. Generating Variation

To be able to investigate the possible variation that might be possible with the retaining of survival and displaying growth method, a series of experiments were performed. From previous research a series of parameters of boundary, survival/birth rules, neighbourhood definitions and number of generation was established. In the first series 1,144 trials were executed. This included all the results from two boundary conditions, one limited and the other unlimited; thirty-seven rules, based on a survival/birth neighbourhood count having a variety of combinations of a maximum of eight cells; four neighbourhood definitions: six locations, four on the same level, one above and one below; the classic twenty-six locations, all adjacent cells on the same level and all the ones above and below; seventeen locations, all the cells on the same level and all the ones below; fourteen locations, diagonals on the same levels and diagonals directly the level above and below. Each of these parameter sets was executed for five, six, nine, and fifteen generations. The initial configuration consisted of eight cells outlining a square arrangement, with the center cell empty. Selected results from this series are displayed in Figure 3.

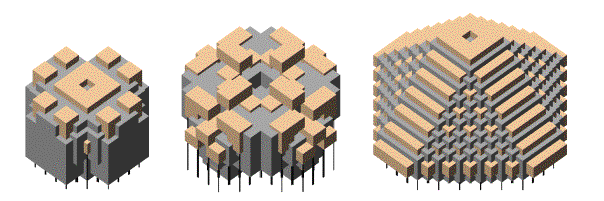
Figure 3. Regular survival series

In reviewing the generated results, some were eliminated; the arrangements that became extinct within the number of generations and the ones that became overly fragmented. Only the ones that retained a fairly connected mass were considered. Architecturally, the process developed connecting masses that further enhanced and highlighted the cellular automata method used to create them. The standard method treats all cells equally, this massing retains the survival history of the cells. When the total series was examined, the possibilities of interesting subgroup arrangements were observed. Further research could find the relationship of these arrangements with the generating parameters exploring the concept of natural occurring styles.

Another series was also investigated that further attempted to introduce a method to increase variety within the results. Figure 4. displays a sample of massings where at every generation a mutation is applied by randomly selecting a new survival/birth rule and neighbourhood count. Architecturally, the concept explores a method to break any evolving pattern so the forms are further unpredictable and offer an even wider range of massings without introducing a natural style. The boundary condition is set to unlimited throughout, with the random selection using all thirty-seven rules and all four types of neighbourhoods. In this series the life span is set to six generations and the space module is represented as a cube. The initial configuration consists of the same eight cells in a square arrangement as before. Over 2,000 random trials were generated.

Figure 4. Mutated survival series

Figure 5. displays an initial sampling of massing developed in the same manner as described above except that the cells are represented as circular volumes and are limited to seven generations.

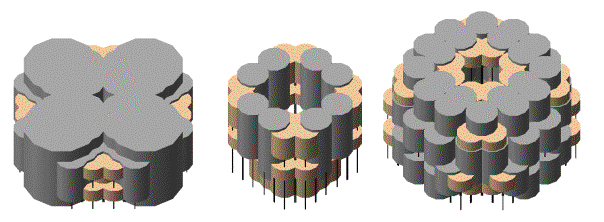
Figure 5. Mutated survival circular series

References

[1] Schrandt, R. and Ulam, S.: 1970, On Recursively Defined Geometrical Objects and Patterns of Growth, in A. Burks (ed), Essays on Cellular Automata, University of Illinois Press, Urbana, pp. 232-243.

[2] Bays, C.: 1987, Candidates for the Game of Life in Three Dimensions, Complex System 1, pp. 373-400

[3] Coates, P.: 1996, The Use of Cellular Automata to Explore Bottom Up Architectonic Rules, Eurographics Conference, Imperial College of Science and Technology, London

[4] Wolfram, S.: 2002, A New Kind of Science, Wolfram Media Press, Champaign

[5] Krawczyk, R.: 2002, The Architectural Interpretation of Cellular Automata, Generative Art, Milan