Generation of Three-dimensional Cellular Automata

Dr. Hong-Sheng Chen, BArch, MArch, PhDArch.

Institute of Building and Planning, National Taiwan University, Taipei, Taiwan.

e-mail: chsh@ntu.edu.tw

Abstract

Cellular automata (CA) are mathematical models for complex natural systems containing large numbers of simple identical components with local interactions. Some researches have demonstrated how to apply this form-making methodology on architectural design, visual design, and even music composing. This paper attempts to introduce some new generative ideas about three-dimensional CA, especially on architectural and music interpretations. For the purpose of generating three-dimensional forms in the computer environment, AutoCAD software and AutoLISP language serve us as a visualization tool.

1. Introduction

Following Wolfram’s original idea [1], CA can be extended to two-dimensional and three-dimensional structures in time sequence. Schrandt [2] and Mar [3] had given some interesting researches on these topics. Emphasizing on its application about form making, Krawczyk [4] demonstrated several architectural interpretations of CA. From such organized patterns, which derived automatically from a computer-aided CA system, we may give suggestions about architectural forms to designers. Particularly in the digital era, we may need a kind of mechanics to generate free forms and to transform the orthogonal facades for architects. Therefore, in this paper, I try to use a professional architectural drawing software to build CA models. It would be helpful for transferring these models to architectural elements.

CA own the power to produce huge amounts of patterned data and very profuse information could be assumed as formats of art. For example, music composition can be thought of as being based on pattern propagation and formal manipulation of its parameters. No wonder researchers started to suspect that cellular automata could be mapped into musical representation in order to generate compositional material [5]. Musical and architectural interpretations are two major interests in this paper.

2. The basic concepts

2.1 One dimensional CA

The research of cellular automata based on computer is one of the earliest forms of artificial life research. Conway's game of life, which sets rules about cells in a grid being on or off, is an original study. In the game of life there is a matrix of cells, and each cell can be alive or dead according to specific rules. We may call it one-dimensional CA. Owing to the similarity to the binary logic of 1s and 0s; it attracts early researchers’ attention about the possibilities for computing.

The rules try to simulate the social relationship and the growth of the natural life. For example, if a cell has too many or too few neighbours it dies, from over crowding or lack of support. If it has a moderate number it lives or comes to alive. Each iteration of the game results in a new pattern of dead and alive cells. The patterns of cells can be mapped to various physical and artistic elements.

2.2 Three dimensional CA

Three-dimensional CA is an expansion of one-dimensional and two-dimensional CA. It deals with more complicated information about the relationship between cells; however, it also provides more spatial data to us. The basic concept of three-dimensional CA constitution in this paper is described as follows. A cell is concerned with its lower-layer neighbours; the amount of its neighbours makes it alive or dead. We overlap the several cell-grid layers and build a 3D-structure. In this computer system, the user may specify a first floor plan or generate the first floor plan by random number. Every upper-floor grid is checked by the sum of its nine lower-floor grids. The rule describes how many lower-level solid cells (0-9) can compose a upper-level cell. Users may specify a rule or let the random number make a rule. The first iteration of first floor life-power was transferred to upper floors, and we even can trace back up side down. With the benefit of computer, this study is built in the environment of AutoCAD and AutoLISP. That’s the reason why we can try many cases using different rules and different sizes of the first floor plan and even different three-dimensional viewpoints very quickly.

2.3 Generation of form and music

The pure mathematical translation of cellular automata into architectural form includes a number of issues that do not consider built reality [6]. The interpretation or translation to a possible built form can be made after the form has evolved. Figure 1 is an example that designers create architectural forms with CA.

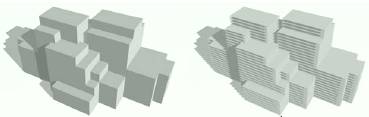
Figure 1. Architectural forms derived from CA. (source: Krawczyk [4])

To transform CA into architectural forms is easier to be realized than to map CA with music, because cells themselves have composed a solid and void space-structure. Some musical questions still could be remained as undetermined “black boxes”; for example, how can a configuration of cells represent a sound granule, and how can the relations between cells represent melody and rhythm? Researchers need mapping methods for translating CA into music composing. Recently, Miranda [7] proposed a Cartesian model in CAMUS to represent a triple, that is, a set of three notes. The model tries to transform spatial data into music; it has two dimensions, where the horizontal coordinate represents the first interval of the triple and the vertical coordinate represents its second interval (Figure 2). It’s one of the known methods to interpret CA into music.

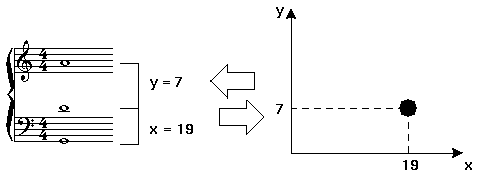
Figure 2. Mapping between music and Cartesian space. (source: Miranda [7])

3. From forming to transforming

In this section, let’s discuss how to create forms and therefore to transform them. The first step is to compose the space structure; in other words, we need a method to use generative rules to create forms. The second step is to transform the structure derived from the first step.

In our computer presentation and simulation, we apply a life and death rule to generate the second floor, third floor, fourth floor and so on. The rule could be denoted as: “0D1L2D3D4L5D6L7D8D9L”, L for life and D for death. V and X also represent same meanings in Figure 3. The number, from 0 to 9, stands for under-level solid neighbour cells in total. For example, 4L means it will survive when there are 4 solid or occupied cells at lower floor; 2D means it will be dead when there are 2 solid or occupied cells at lower floor. The colours represent the amount of cells. We use AutoLISP programs to generate 3D structures. We may use AutoCAD command to see this basic structure from different view-angles, and to “shade” this structure (Figure 4).

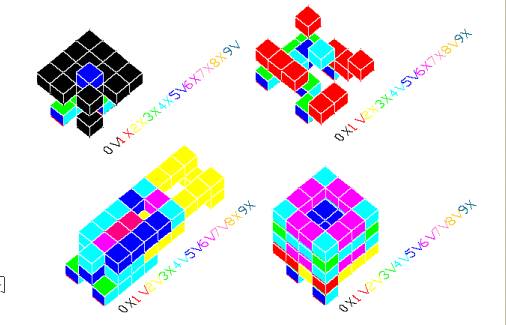
Figure 3. Basic examples of three-dimensional CA derived from different rules.

Figure4. A basic structure (left) and a shaded structure (right).

We give every cubic cell different colour for representing its total lower-level neighbours. For example, red stands for one solid cubic under it’s lower-level neighbours (within 3 x 3 grids); yellow for 2, green for 3, bright blue for 4, dark blue for 5, magenta for 6, pink for 7, brown for 8, grey for 9, and white for zero.

3.1 Architectural form

Our CA system provides a basic construction of solid and void space. It could be an interesting inspiration for designer to create the composition of space. Like Figure 5, we embed columns in a cellular structure, and make it look more like a real construction. Here, allow me to explain again, the colour of every cube has its meaning. The colour is determined by the total of its lower level solid cells; therefore it is not just for fun. The ground level has no lower level; therefore, we give the 6 faces of a cell different colours.

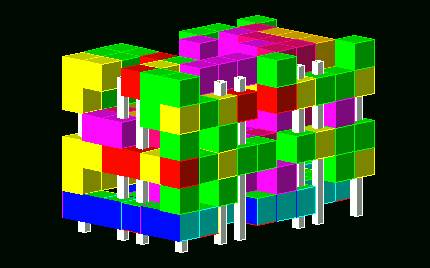
Figure 5. Embed columns in a cellular structure.

3.2 Transforming

Following is an idea of transformation. I put two strings into every cell for stretching its cubic-box contour (Figure 6). The strings connect four diagonal corners of a box. When a generate program runs, the simulation system will stretch the lengths and change the directions of these strings based on random numbers; therefore the whole structure could be transformed into a kind of “free” form. It is able to break the original orthogonal boxes when this program runs. The facades of a structure will be twisted seriously if we use this transforming rule many times. That’s the reason why I put only two strings inside a box, because more strings stretched in a box will destroy this box and make it unrecognisable.

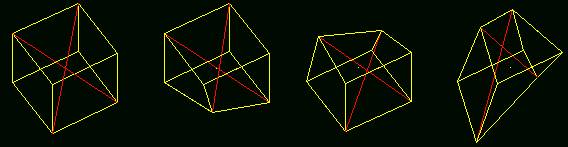
Figure6. A box with normal strings and three boxes with stretched strings.

In fact, when the simulation system stretches a string, it will stretch all the boxes whose corner is connected with this string’s two ends. Therefore, the whole wire-frame structure is transformed. Figure 7 is an example to explain the original orthogonal structure and two transformed structures after applying different times of stretching-rules.

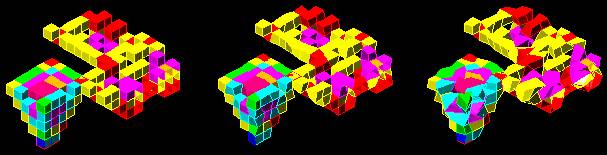
Figure7. An orthogonal structure and two transformed structures.

3.3 Generating different size cells

We may change the size of these cells with random numbers, which give the boundary of maximum and minimum lengths of every box (Figure 8). It vivifies the composition of a structure, too. This kind of expressions could be a good suggestive composition for designers, and for further manipulation.

Figure 8. Random cell size structures.

On the other hand, it may give some suggestions and inspirations to design building’s elevation. (Figure 9.) In this section, we may realize the diversity and creativity of three-dimensional CA. With the assistance of AutoCAD and AutoLISP program language, we may generate many space structures, and test interesting solid/void possibility in computer.

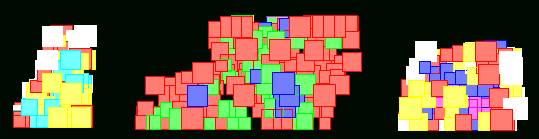
Figure 9. Simulation of architectural elevations.

As we know, a box has six faces. In the above-mentioned examples, all boxes are closed. However, we may open some faces of these boxes, or even erase some boxes in a structure if you do not like so many boxes, to create an open-faced structure. Demonstrating the inner composition of cells, we may display a construction with cubes and plates (Figure 10).

Figure 10. A structure with some opened boxes.

3.4 Random-sized cell structures

In this section, we use two above-mentioned methods together to create free-form random-sized cell structures. Obviously this generation can transform the original form a lot; the result seems more similar to natural organizations than artificial works (Figure 11). For example, it may look like villages that are located on a hill. Figure 12 has two pictures of Greek villages, Fira and Oia. There are some interesting similarities between our generative cell structures and these natural grown villages. For example, they both have cubic contour, plane roofs, vertical walls, horizontal layers, hierarchy and organic organization in particularly.

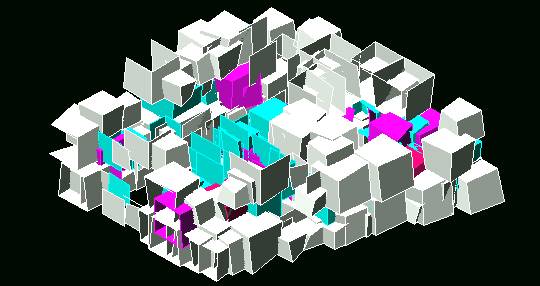
Figure 11. A structure with random-sized and twisted and opened cells.

Figure 12. Two organic cubic structured villages. Left: Fira, Right: Oia; Santorini, Greek.

4. Musical interpretations

Modern music has become an interesting discipline for the application of new scientific discoveries inviting composers to combine artistic creativity with scientific methods [7]. Based on the development of computer techniques, more and more composers turn to the sciences to supplement his or her compositional models. Particularly, artistic creations share the same sources of mathematics, nature, and biology, etc. By the same token, scientists also seem to show interest in the organisational principles to be found in music and other arts.

CA are computer modelling techniques widely used to model systems in which space and time are discrete, and quantities could be displayed as a finite set of discrete values. Therefore, the proposed three-dimensional CA could be a generative machine, which is able to create multi-layers cells. If we regard these cells located at ground level as fundamental tones, then we may apply generative rules to create upper levels. Take Figure 13 for example, we translate a piece of music into cells, and the location of cells match their melody and rhythm. In other words, we may see the ground-floor plan (left-up) as a piece of music. The second floor (3,4), third floor (5,6) and fourth floor (7,8) are generated from ground floor (1,2).

In theory, we may derive as many levels as we wish. Finally, these cell-plans composed tones, chords and melodies. If we use another rules, perhaps the results of generation and the melody will be very different. In this case, maybe it is not a good piece of music for everyone; however, it’s an interesting way to generate not only cubic boxes but also music.

We may use it in another way. If we take a whole piece of music as a very long ground-floor plan, we may generate a whole piece of music at one time. With the assistance of computer techniques, it would be a quite interesting way to compose new music.

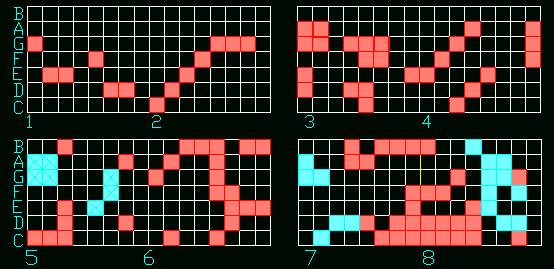
Figure 13. Floor plans representing a piece of music.

5. Conclusions

The results of the cellular automata interpretations are very encouraging. They are good evidences that both architectural and musical forms can be successfully modelled by using cellular automata. Nowadays designers probably have learned to shift their issues from forming to transforming [8], and from designing one artificial product to creating a family of art [9]. However, we still need more ideas about generative design methods in various artistic domains. In architectural experiments, this paper provides several ideas about space transformation and construction. In musical experiments, this paper tries to translate spatial relations to compose music. It should be noted that it is not the only way or correct way to utilize CA. There ought to be many interesting or global principles creating both architectural and musical forms. Perhaps the next step would be to integrate CA and neural systems in order to study the relationship between form making, design thinking, and behaviour controlling. In general, we found that a CA system could produce profound data sources until the next cell generation dies. We think that in this case it might need a kind of rebirth or regenerative model for continuing to grow cells. As architecture and music are primarily cultural-related phenomena, sometimes we need to think about how to employ CA techniques that can produce results sensible, content, or at least reasonable. Otherwise it is just an interesting computer game.

References

[1] Wolfram, S.: 1984, Cellular Automata as Models of Complexity, Nature, 311, pp. 419-424

[2] Schrandt, R. and Ulam, S.: 1970, On Recursively Defined Geometrical Objects and Patterns of Growth, in A. Burks (ed), Essays on Cellular Automata, University of Illinois Press, Urbana, pp. 232-243.

[3] Mar, G. and Denis. P.:1996, Real Life. International Journal of Bifurcation and Chaos, Vol. 6, No. 11, pp. 2077-2086.

[4] Krawczyk, R. J.:2002, Architectural Interpretation of Cellular Automata, Generative Art Conference, Milan, Italy. pp. 7.1 – 7.8

[5] Miranda, E. R., CAMUS-- A Cellular Automata Music Generator, http://website.lineone.net/%7Eedandalex/camus.htm#intro

[6] Krawczyk, R.: 1997, Programs as Pencils: Investigating Form Generation, ACADIA 1997 Conference, Association for Computer-Aided Design in Architecture.

[7] Miranda, E. R. Evolutionary Music Research -- Sound Synthesis and Composition, http://website.lineone.net/~edandalex/celautom.htm

[8] Soddu, C.: 2000, From Forming to Transforming, Generative Art Conference, Milan, Italy.

[9] Fischer, T. and Herr, C. M.: 2001, Teaching Generative Design, Generative Art Conference, Milan, Italy.