Very small Elements in very large Arrays

Prof. H. E. Dehlinger, Dipl.-Ing., M. Arch., PhD.

Kunsthochschule Kassel, Generative Design Lab, University of Kassel, Germany.

e-mail: dehling@uni-kassel.de

Abstract

Embarking on a minimalist concept of algorithmic generation, pen-plotter-drawings have been generated, which use very small elements in very large arrays. The calligraphic quality of the drawings relies on a massive repetition of "standards" within a matrix. Random processes are used to disturb and to contaminate the regularity of this matrix. The resulting drawings are complex and unique. They demonstrate the power of a simple concept, based on a minimal set of easily identifiable elements.

1. Generative Processes and Design

In any kind of generative design process, answers must be given to two important questions:

(a) What is intended (what is the pursued concept, the idea)?

(b) Which system of generative rules - which generators – are suited to produce (a)?

Naturally, the generative system employed should meet the designers intentions as precisely as possible. This is not always simple for different reasons. All design problems have specific and well-known characteristics, and since generative design - despite its heretic and radically different approach - is within the realm of design, it will still face these very same problems, which are characteristics of design and which are responsible for the difficulties and dilemmas of designing at large. Some of these difficulties, which we find in all design problems, are for example [1]:

(1) There is no definite problem formulation

(2) There is no stopping rule

(3) Solutions are not true-or-false, but good-or-bad

(4) There is no immediate or ultimate test of a solution

(5) Every solution is a “one-shot operation”; because there is no opportunity to learn by trial-and-error, every attempt counts significantly

(6) There is no enumerable (or exhaustively describable) set of potential solutions, nor is there a well-described set of permissible operations, that may be incorporated into the plan

(7) Every design problem is essentially unique

(8) Every design problem can be considered to be a symptom of another problem

(9) The existence of a discrepancy, representing a design problem can be explained in numerous ways. The choice of explanation determines the nature of the problem’s resolution

(10) The designer has no right to be wrong

The invention of a generator (the design of a design machine) represents the actual challenge within generative design. Any such generator is not objectively right or wrong, it is more or less good or bad in the eyes of a respective viewer, inspecting the results it generated. The ideologies, value systems, aesthetic views, etc. which are hidden within any generator, represent very personal forms of knowledge, and the designers of these systems carefully lock this knowledge away from any public access.

2. Performance of Generators

As a measure of performance p of a generator (with regard to the quality of the generated output), we may use the ratio of the number n of good (useful, acceptable, spectacular, unexpected etc.) outputs generated over the number N of attempts to generate them:

p = n / N (1)

A goal is to get close to the value 1 for p; e.g. to produce for each generative run a “good” (useful, acceptable, spectacular, unexpected etc.) result. What we regard as good and how we measure the quality of a generated output, is a different question of its own. In a favorable case, the generator contains sophisticated measures, acting like filters through which only the “good” solutions are allowed to pass. In an unfavorable case, the evaluation of generated results is a separate, post generative process, where for each generated output it is to be decided, whether it will be rejected, or accepted as useful. For the drawings discussed here, p is approximately 1 / 3.

When we analyze generators with reference to their evaluative schemes we find an open list of approaches, for example:

(1) an explicit performance function (like greatest velocity, lightest weight, greatest stability etc.) is employed. Such performance functions are widely employed in optimization techniques

(2) a large number of assumptions and of personal preferences are elevated to the status of axioms and parameterized for manipulation in various ways

(3) ad hoc input from the context of the problem space is used to feed a generator

(4) a set of procedural rules is operating on a carefully constructed morphological structure

(5) a set of transformations is applied to an arbitrarily chosen input (traffic data, weather forecast, my left shoe, the sound of an engine, the sequence of cigarette brands in a vending machine, a song, movements in a video clip, an image drawn from the environment, etc.)

(6) a set of variables resulting from a strict rational analysis is manipulated by a player following specified rules

(7) etc.

Whenever judgment comes into play, our decisions are grounded on “Weltanschauung”. We unavoidably disembark from objectivity and have to resort to argumentative persuasion. And judgment (evaluation) is everywhere in generators. The seemingly trivial selection of a pair of coordinates x,y for further processing may draw on a preference structure which is hidden further down in the generator, where allowable ranges may have been explicitly stated as a consequence of some other chain of considerations.

But this is no harm as long as no claim of “optimum”, rightness or truth is made. It is one of the astonishing experiences encountered in the generative approach that surprisingly unexpected results may pop up, which trigger our fantasy and our imagination and which are leading to unexpected new viewpoints.

3.Small Elements in large Arrays

I talk about drawings, which are produced with a generative program, and which are executed on pen plotters. Pen plotters, a type of first generation computer periphery, have become extinct and they have been replaced by other, more efficient printing technologies. There is however reasons to prefer them to printers, particularly for art motivated output. The calligraphic quality of a line produced mechanically by a pen is of special interest for the type of drawings discussed here.

The experiments generating such drawings, and the generative systems, which have been designed to produce them, are regarded, as exemplary models for the design of generative systems as such, because they display all the difficulties of such systems, but they do this in a comprehensive, easily understood manner.

It is regarded an important goal of these experiments, to program generators which produce results with a minimum of effort, and I like to categorize this approach as “Generative Minimalism”. The resulting drawings should be of high calligraphic quality and leave ample room for associations and interpretations. As a justification for choosing the topic “Small Elements in Large Arrangements” I refer to the following list:

(1) Such elements are found in many different forms and on many scales of our environment such as: In views into a landscape, the grasses on a meadow, in the branches of trees, in the leaves on trees, the pebbles on a beach, in the asphalt cover of roads, on walkways, in the tiles of roofs, as stones in old and new walls, etc. Small elements in large numbers and arranged in endless varying patterns are very frequent in nature and in man-made environments, and they are familiar to us.

(2) “Repetition” is an interesting generative operation. To generate a structure of order using identical elements is possible with a very simple generative rule. The application of such a principle is in line with the intended “Generative Minimalism”

(3) The use of small, simple shaped elements in large arrays is an experimental scheme, which can be easily extended to complicated arrangements with any number of elements (of any complexity)

(4) For the design of the generators, no natural limit is in existence. Modeling such generators sheds light on the design problem of generative systems in a very general sense

(5) Arrangements of elements, which we find in nature, are rarely “geometrically clean”. More frequently, they are disturbed and contaminated, which is exactly one of the appealing aspects to us, when viewing such semi orderly structures.

(6) For the generative production of disturbances in the arrays, coincidental shifts of the elements are performed. Shifting elements may also be considered a minimalist generative operation, which again is in line with the intended goal of to follow a “Generative Minimalism”.

The illustrations [1], [2], [3] show some examples of small elements drawn from nature, where they are found in large numbers.

Fig.1 Stones in a river Fig.2 Trees against sky Fig. 3 Leaves on the ground

The illustrations [4], [5], [6] show some attempts to derive abstractions from the above for use in the drawings.

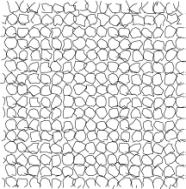
Fig. 4 “Potatoes” Fig.5 “Circles” Fig. 6 Short strokes

The illustrations [7], [8] and [9] show some examples of generated drawings, which use such elements.

Fig.7 Example of drawing Fig. 8 Example of drawing

Fig. 9 “Cheer” (2003)

4. Summary

A summary of the discussed approach and its results is formulated in the following statements:

(1) small, identical or slightly varying elements in large numbers are placed in dense, contaminated arrangements

(2) elements and arrangements where collected from nature (environment), stored photographically, converted and abstracted, then used as suggestions for experiments

(3) Generators for arrangements were programmed in Spitbol [2], which generated the HPGL-code [3] for the plotter drawings.

References

[1] Horst W. J. Rittel, Melvin M. Webber, Dilemmas in a General Theory of Planning, Policy Sciences 4 (1973), 155 – 169.

[2] Robert B.K. Dewar, Mark B. Emmer, Robert E. Goldberg, MaxSpitbol, The SNOBOL4 Language for the Apple Macintosh Computer, Tutorial and Program Reference Manual Catspaw Inc., 1989.

[3] Hewlett-Packard Company, Interfacing and Programming Manual, San Diego, 1983.