The Groningen Twister
An experiment in applied generative design
Abstract
This paper
describes a collaborative project between the chair for
Computer Aided Architectural
Design (CAAD) at the ETH Zurich, the design team of Kees
Christiaanse Architects & Planners (KCAP) in Rotterdam, and
an engineering team of Ove Arup & Partners in Amsterdam and the chair for
Computer Aided Architectural Design (CAAD) at the ETH Zurich. The project
was initiated in February 2003.
The aim of the project was to develop a CAD-tool which would help the architects of KCAP to solve a complex design task: Underneath a pedestrian area that links the main station to the city center of Groningen/NL, there was a need for parking space for approximately 3000 bicycles. To support the concrete slab of the pedestrian level, the desired design called for more than one hundred columns of different sizes to be placed in a random pattern, but to be then sized and controlled according to structural, functional and aesthetic needs.
To solve this problem, a software was developed at the chair for CAAD that simulates a growth process for the columns. The distribution of the columns is defined by structural rules, provided by ARUP’s engineers, as well as functional and design rules provided by KCAP’s designers. The results are presented to the user as a three dimensional, dynamically evolving model. At any time during this process the user is able to control the model on the screen interactively. The user can control the process in two distinct ways, on the one hand by directly controlling the placement of single columns, on the other hand by adjusting various parameters that define the properties of the columns and the environment. The system provides real time feedback, as the column distribution tries to adapt to the changed configuration. This allows the user to test various alternative solutions in very short time. After a stable and satisfactory condition is achieved, the resulting column locations can be exported for construction documents in various digital file formats.
The final architectural design, based on the output of the software, has been approved and construction work in Groningen is about to start.
1. Introduction
In the year 2000 Kees Christiaanse Architects & Planners (KCAP)
[[1]]
and the University of Kaiserslautern started the “Kaisersrot” project [[2]] to develop new methods of
urban development based on “bottom-up” principles. To allow rapid testing of design
rules, various CAD software tools were programmed which allowed to describe
inter-dependencies in urban structures and iteratively generated urban plans
according to rules and user interactions. In 2001 the project was merged with
the Chair for Computer Aided Architectural Design (CAAD) at ETH Zurich [[3]]
and the fruitful cooperation resulted in a number of successful applications,
particularly the “Schuytgraaf” project in Arnhem/NL.
Early in 2003 a design team of KCAP approached the CAAD chair with another, different problem. This time it was not an issue of urban design but a complex architectural design task to be solved. The following text describes – in the manner of a workshop report – the solution of this task, which was achieved by a specifically developed generative standalone CAD-Tool – the Groningen Twister.
2. How to design a forest of columns?
In the city of Groningen, in northern Holland, KCAP is redesigning a
public square in front of the train station: the Groningen Stadsbalkon. In
order to achieve a better link between the city center and the station, a bus
terminal was moved to the side and gave way for a spacious new pedestrian area
and a semi-subterranean parking lot for 3000 bicycles underneath.
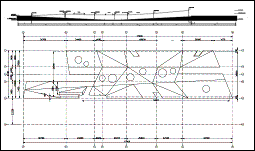
The final design consists of a concrete flat slab with large holes for letting light down to the basement and to enable two large trees to grow up. It has a number of incisions for ramps and stairs. Some edges of the slab rest on the ground, others loom in the air, flexing the pedestrian area into a long sweep over the whole length.
To give the whole structure an additional notion of lightness, the
design called for it to be supported on
a field of slim concrete columns. The complex outline of the slab and the
already defined paths and bicycle stands in the basement made it difficult to
place the columns on a regular grid. As a result, it was decided to locate the
columns randomly, giving the impression of a “column forest”. To re-enforce
this impression, the design called for the columns to be made with different
diameters and random degrees of tilt.
In a first rough calculation, the engineering team at Ove Arup in Amsterdam estimated that it would take about one hundred columns to hold up the slab and stay within the budget. But then the problem was: where to place the columns? There were too many degrees of freedom (column location, tilt angle, column size) and at the same time too many restricting rules (holes, incisions and paths to avoid, bearing capacities, optimum column distances) influencing each other and preventing to design a structurally and aesthetically working solution in reasonable time. A brain twisting task, at least if you tried to do it by hand.
3. Letting them grow
There has been much research into the use of artificial intelligence in design and architecture since Bill Mitchell stated in 1977 that a “comprehensive CAAD system” had to perform the function of automatic generation of solutions to well defined problems[[4]]. Recently, research into the principles of artificial life (such as cellular automata, swarm systems, and genetic algorithms) has proven to be a very reasonable way to deal with the ill-defined (or not adequately definable - due to aesthetic demands) problems of architectural design [[5], [6], [7]]. The chair for CAAD at ETH Zurich has gained some very positive experiences in the field of generative bottom-up principles with the already mentioned Kaisersrot project. So it was clear that a similar solution could be the answer to this problem: A software simulation of “living columns” that are able to grow on the best locations within a common habitat.
3.1 The habitat
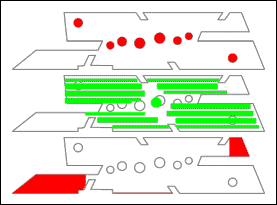The living space for the columns is well defined by the functional
and conceptual constraints described in chapter 2: The top ends of all columns have to be located
within the outline of the slab while avoiding the holes and incisions. In some
areas the slab is lying on the ground, so no columns are needed there. The
bottom ends of the columns should seek the areas of the bike stands to get out
of the way of pedestrians and bikers. As a result, the habitat actually
consists of two layers: the slab where the top ends of the columns have to find
their locations, and the floor plate where the bottom ends have to do so. Fig. 4Fig. 4Fig.
4 shows the habitat with the slab outline, the
attracting areas in green, and the repelling areas in red.
3.2 The organisms
The columns are
generated initially asrepresent particles in a swarm system: Each
column in the system is an autonomous individual, exploring the habitat and
reacting to its neighboring columns .
According to the two layers of the habitat (see 3.1), the column model consists of two independent parts.
The bottom end can move freely within the ground plane of the model, whereas
the top end can move in the plane described by the slab. The actual column
position,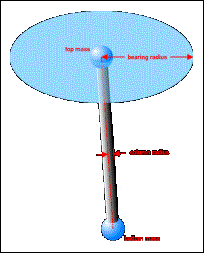 
length and tilt is defined by the connecting line. It has to be assured,
that the tilt angle stays below the assigned maximum.
This behavior is easily described by a spring-mass-system: punctual masses are connected by a virtual spring that pulls depending on the distances between the masses. In our model each organism is composed of two masses which describe the top and bottom end of the column and a spring in between. The force of this spring is proportional to the horizontal distance and, since the move of the masses is confined within the two planes of the habitat, they are drawn to positions above each other.
3.3 Interaction
The columns are interacting with their adjacent columns as well as with the surrounding habitat following the same simple principles of attraction and repulsion by virtual springs. If they come to close, the top masses of each column are repelled by the slab outline, the holes, and the areas without cellar. The bottom masses are attracted by the closest bike stand.
To get the desired effect of distributing the columns, they seek to stay at a certain “social distance” to each other. This distance is defined by the maximum spanning distance of the slab and the bearing capacities of the respective columns. The bearing capacity of a column defines a circle around the top end marking the area where column is able to support the slab (see Fig. 5). Neighboring columns therefore have to be aligned so that their radii touch or overlap slightly. This is also accomplished by virtual springs that push or pull between their respective top masses.
The result is a complex system of masses and springs that can be analyzed in a non-linear time-step simulation, as described by Martini [[8]]. To prevent resonance catastrophes and to promote a termination to the process, an additional damping factor is introduced which induces a certain friction on the movement of column masses.
4. Implementation
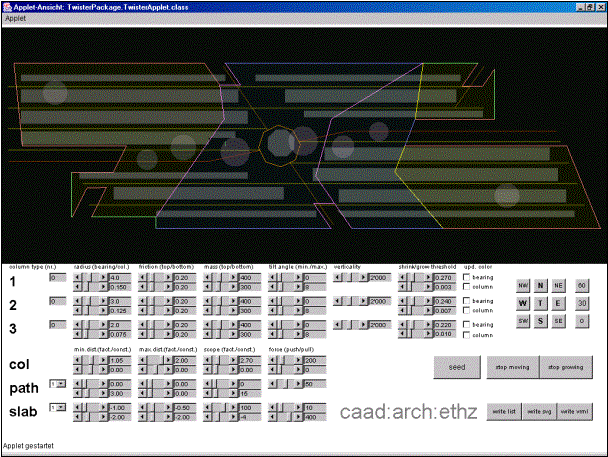
One of the main goals of the project was to create a highly interactive application that would allow the architects to directly influence the outcome of the simulation process and see immediate feedback on the decisions they took. Therefore it was necessary to have a graphical representation of the whole model, preferably in three dimensions, and very short response times. Since the application had to run in a multitude of different environments (at the CAAD chair, at KCAP and at ARUP), it was also necessary to address compatibility issues. Development time for the project was also very short, and it was necessary to quickly exchange new versions of the software over long distances, so after a few tests it was clear that the software could and should be programmed in Java. The Java 3D API provides a very powerful and effective 3D programming interface which at the same time is very clearly structured and easy to use. It runs on Sun, Windows and Linux systems with OpenGL and DirectX graphics adapters, and the Java executables – especially in the Java-Archive format (JAR) - are very lightweight, so the compiled programs could easily be exchanged via email. [[9]]
|
max. rad. |
approx. |
|
|
150 |
2.0 |
15 |
|
250 |
3.0 |
35 |
|
300 |
4.0 |
50 |
4.1 Column Specifications
The
specifications of the columns were given by Arup as shown in Tab. 1Tab. 1Tab.
1. There are three types of columns with different
diameters and bearing capacities. The maximum radius of the column results from
the bearing capacity and defines the distance between the columns as shown in 3.2. The tilt angle of the columns was limited to 10
degrees so that this factor could be ignored in structural calculations. Also
the height differences between the ground plane and the slab were not cared for
and an average height of 3.0 meters was used throughout the habitat. The
approximate number of columns needed was estimated by Arup based on the maximum
radii and the building budget which would only allow for a certain number of
columns.
4.2 Prototype: arranging columns
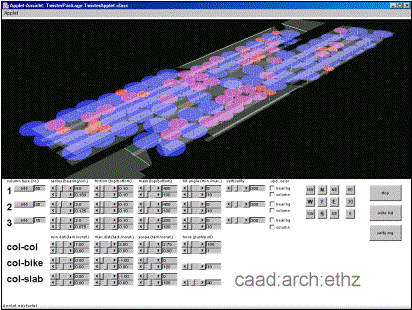The first version of the software was a simple particle system: the
columns as described in chap. 3.2 could be “thrown” into the middle of the habitat and
immediately started to arrange themselves according to the definitions. The
user could pick and drag a single column and change various parameters
influencing the interaction amongst the columns and between the columns and the
habitat (slab, bike stands, holes). The viewpoint could be changed via mouse
dragging, keyboard navigation and various preset viewpoints. The results could
be exported as two dimensional SVG graphics and as comma separated lists of
column locations.
Results
The results
achieved with this first version were very encouraging. The columns managed to
arrange in very reasonable patterns, as is shown in Fig. 6Fig. 6Fig.
6. With some tweaking of the parameters, stable
conditions could be reached in very short time. The frame rate of the
simulation was high enough to directly interact with column numbers up to 150
on an average notebook without hardware graphics acceleration.
But there still were some flaws. Besides pushing each other there was no real interaction between the columns, and they were not reacting on their environmental situation. Once assigned, a column could not change its type anymore. So the arrangement of the column-types was only dependant on the random placement in the beginning and the user who could drag single columns to new (better) locations. There were also big structural problems in the center of the slab where no bike stands were planned, so the columns had no place to position themselves. Furthermore, after they had been shown the first version, the engineers at ARUP came up with some additional structural constraints. So the next version of the Groningen Twister was planned with some major changes.
4.3 Final version: Growing columns
While testing the prototype, construction details appeared which had not been part of the initial considerations: Two expansion joints across the middle of the slab were necessary. Parts of the slab were interspersed with glass blocks which influenced the spanning capacity and therefore the maximum column distance in the affected areas. Some the edges of the slab, the edges of the holes, and the expansion joints, also required different structural responses with regards to cantilevering and column distances.
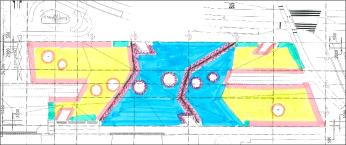New model of the slab
To integrate
the new structural rules into the system, a different model of the slab was
necessary: It now consisted of five independent partitions, separated by the
joints and the border line between areas with and without glass blocks. In
reaction to the differing structural demands in various regions of the slab,
the partitions, their edges and the holes were grouped into five categories
with independent parameters as shown with different colors in Fig. 7Fig. 7Fig.
7.
Paths instead of column areas
To avoid the column-less area in the middle of the slab, the criteria for the placement of the lower column ends was changed completely. The task – to keep columns from obstructing the paths – was now modeled directly: Instead of being attracted by the bike-stand areas the columns now are repelled by the paths, which are defined by their center lines. According to their traffic volume the paths are grouped in three categories with different repelling forces, ranging from the main bike route through the center, to the secondary paths at the stairs, and the small access paths between the bike stands.
Growing columns
The most important change from the prototype was the completely different approach in distributing the columns. By making them pressure sensitive and able to change their type, an actual growth process was possible. Instead of assigning a column diameter and bearing radius from the beginning, the columns were now able to adapt to their surroundings by changing their size autonomously.
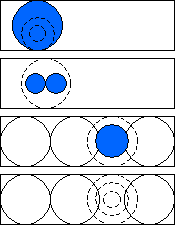A column that is too far away from its neighbors detects a low
surrounding pressure and starts to grow in discrete steps, matching the column
types defined in chapter 4.1 (see Fig. 8Fig. 8Fig.
8a). If it reaches the largest possible state and still
has no close neighbors, it splits into two small columns which both start
growing again (see Fig. 8Fig. 8Fig.
8b). If a column gets to close with its neighbors or
the edges of the habitat the resulting pushing increases the pressure and it
starts shrinking in just the same way (Fig. 8Fig. 8Fig.
8c). And if it reaches the smallest state while the
pressure remains high, it finally dies (Fig. 8Fig. 8Fig.
8d). Thus, by “seeding” a single column the whole area
of the slab is filling up with columns over time.
The pressure threshold values for the growing and shrinking can be adjusted for each column type independently, so it is possible to influence the distribution of columns to the three types. In some regions of the slab where the spanning capacity is lower due to glass inlays, the growth is restricted to the two smaller column types.
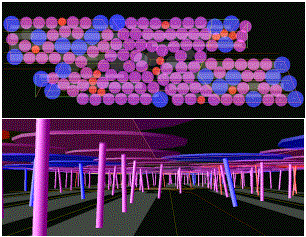
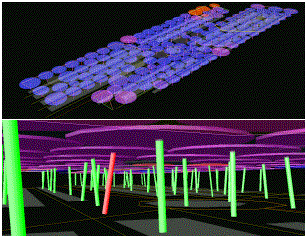Results
The results of
this version proved to be much better than that of the prototype. After
“seeding” a single column into each of the five slab partitions, they start
growing, splitting and eventually filling up the whole area. The column types
adjust to the necessities of their location (see Fig. 10Fig. 10Fig.
10). After a few tries it was possible to adjust the
default parameters so that the structural constraints were fulfilled to a high
degree. Various color coding schemes proved to be helpful. For example; itIt is for example possible
to tint the columns relative to their kinetic energy (see Fig. 11Fig. 11Fig.
11a) or mark those columns which exceeded the maximum
tilt angle (see Fig. 11Fig. 11Fig.
11b). In very short time the architects at KCAP were
able to handle the various parameters quite well and produced numerous versions
of the column layout. The best version was exported to AutoCAD and used as a
basis for the further development of the final design (see Fig. 12Fig. 12Fig.
12).
A few problems turned up in the working phase, which could not be
completely solved due to lack of time: The discrete growth of the columns
caused the phenomenon that the total kinetic energy of the system increased
every time a column changed its type. Either a growing column applied a greater
pushing force on its adjacent columns, or the neighbors of a shrinking column
suddenly had more room to move and therefore a higher potential energy to be
turned into velocity. In tight situations (like in the upper right corner in Fig. 11Fig.
11a) this lead to very unstable conditions with high
velocities and a high type-change rate. Also it was difficult to prevent
columns from exceeding the maximum tilt angle when their lower ends came too
close to a path. The linear increase of the erecting force was sometimes much
lower than the accumulated pushing and pulling forces the attractors and
repellors applied to the column ends.
5. Summary and future work
The basic
concept for this generative tool is direct interaction. The software is seen
looked
upon as an interface which maps the different views of the project
participants onto a single model and therefore allows a very different mode of
communication about the project. In this case the architects at KCAP stated
their design idea based on a flat slab and the notion of a “column forest” and
the engineers at ARUP provided a set of rules of thumb which would ensure that
the design stayed within structural possibilities, based on their notion of a
concrete structure. Programming these rules into a plain simulation system and
allowing the user only to start and stop the process would reduce the task to a
mere optimization problem with a probabilistic outcome based on the quality of
the software design. But if the simulation is highly interactive, so that the
user can influence the process at any given time, it becomes a true design
tool. This tool allows the architect the freedom to decide about the aesthetic
and functional aspects of the design, while steadily, but uncompromisingly,
pushing the results to a state that satisfies all of the structural rules..
There have already been requests for studies on similar projects. To be able to rapidly develop further simulation studies it is planned to develop a software toolkit based on the most valuable insights gained from this experiment.
Steady growth
The sometimes explosive increase of kinetic energy in the system as described in 4.3 poses a big problem. The system never reaches a stable equilibrium as long as the deceleration by damping is lower than the acceleration by type-change of columns. To simply turn up the damping parameter only leads to suboptimal states because the columns are handicapped in arranging their positions. To turn off the growing and shrinking on the other hand prevents them from adjusting their size. The dilemma could be resolved by the introduction of a continuous growth of the bearing radii. The resulting column diameters could still be discrete, some of the columns would then simply be over-dimensioned.
User Interface
Since the target user group of design tools like the Groningen Twister is architects in a professional environment, the software has to become more user friendly and ergonomic. It has been criticized by the users that there was no possibility to save intermediate states of the evolving structure to be able to start later explorations from there on. To be able to quickly react on design changes, import filters for CAD files are needed. Also a direct output to CAD formats is highly desirable.
Statistics and measurements
In the current
version, the designer has to rely on the software to deliver “correct”
solutions without having a detailed control mechanism to see whether structural
needs are fulfilled. What the Groningen Twister is missing lacking up to
now is a quantitative “fitness measure” of the achieved solution. Fitness
measures could, for example, be a comparison of the number of columns required
to cover the whole slab, the amount of “overlapping” bearing radii, the
exceeding of tilt angles, and so on. This would allow a precise identification
of the structurally and functionally best solution and leave the aesthetic
judgement to the designer. The inclusion of this quantitative evaluation would
also make automatic parameter testing possible or the evolvement of solutions
by genetic algorithms.
Acknowledgements
This work would not have been possible without the support of the following people:
Ÿ
Prof. Dr. Ludger
Hovestadt,
head of the
CAAD
chair at
ETH
Zurich
Ÿ
Oliver Fritz and
Markus Braach, the Kaisersrot team at CAAD/ETH Zurich
Ÿ Andy Woodcock, architect and project manager, and his team at KCAP Rotterdam
Ÿ Arjan Harbraken, engineer and project manager, and his team at ARUP Amsterdam
ŸOliver Fritz and Markus Braach, the Kaisersrot team
at CAAD/ETH Zurich
Figures
Fig. 1: Kaisersrot
Software for urban planning
Fig. 2: Model view
of the Groningen Stadsbalkon
Fig. 3:
Longitudinal section and outline
Fig. 4a-c: slab
outline with holes, bike stands and areas without cellar (top to bottom)
Fig. 6: Screenshot
of the Groningen Twister prototype
Fig. 8a-d: A
column is growing, splitting, shrinking and dying.
Fig. 9: Screenshot
of the Groningen Twister before adding columns
Fig. 10a-b:
Twister in action, color coding by column type
Fig. 11a-b: Color
coding by kinetic energy (top) and excessive tilt angle (bottom)
Fig. 12: Rendering
of the final layout (by kind permission of KCAP)