Genetic
Algorithm for the Evolution of Feature Trajectories in Time-Dependent Arts
David Birchfield, DMA, MA, BM
Arts, Media and
Engineering, Arizona State University, Tempe, Arizona, USA.
e-mail: dbirchfield@asu.edu
Abstract
Especially in generative art, the creation of perceptible and compelling large-scale forms and hierarchical structures that unfold over time is a nontrivial challenge. Nonetheless, this is an important goal for artists, such as musicians and video artists, who work in time-dependent mediums. In my work as a composer, I often sketch curves and lines that plot the trajectories of how musical features will develop throughout a given piece of music. For example, I might imagine a piece that exhibits a timbral evolution moving from bright to dark and a density trajectory from dense to sparse. I have found that the design and implementation of multiple, independent musical feature trajectories allows for complex musical structures to emerge, and I have worked to design this capability into generative systems for the composition of music. In this paper I describe the motivations and goals associated with the design and implementation of a hierarchical, coevolutionary genetic algorithm comprised of a population of musical components. I concentrate on the aspects of the algorithm which enable the automated generation of feature trajectories through the use of artificial intelligence and an expanded definition of the genetic feature.
Keywords
Generative Art, Music, Computer Music, Genetic Algorithm, Evolution, Music Theory, Music Cognition, Music Perception, Algorithmic Composition
1. Introduction
In my
work as a composer, I often sketch curves and lines that plot the trajectories
of how musical features will develop throughout a given piece of music. For example, I might imagine a piece that
exhibits a timbral evolution moving from bright to dark and a density
trajectory from dense to sparse.
Simultaneously, the amplitude level might rise from low to high, and
return to a moderate level toward the end.
I hope to create structures such as timbral motives that evolve along an extended contour. I hope to create sequences of rhythmic distortions as defined by a subdivision value’s contour. I want to be able to create meta-contours that drive the overall form of the music as well as local gestural contours which can serve as motivic structures. Furthermore, I want to be able to define independent contours for rhythm, timbre, amplitude, and frequency for any given level of the musical structure. Using sharp contours I want to be able to probe the extremes of each feature of the system and control the extent to which these extremes are reached.
I have found that the design and realization of multiple, independent musical feature trajectories, such as those described above, allows for complex musical structures to emerge. Such structures can support large-scale forms of durations ranging from ten to thirty minutes. I have worked to design this capability into a generative model for the creation of music. In this paper I describe the design and implementation of a hierarchical, coevolutionary genetic algorithm comprised of a population of musical components. I concentrate on the aspects of the algorithm which enable the automated generation of feature trajectories through the use of artificial intelligence and an expanded definition of the genetic feature.
I
will first discuss my motivations and musical goals for creating the
model. I will explain my reasons for
implementing a genetic algorithm. I
will illustrate the hierarchical organization of musical population. I will then discuss the expanded scope of
the genetic feature and describe how this allows for the emergence of
sophisticated feature trajectories over time.
I will explain the role that artificial intelligence plays in the
interactions between musical components, and finally, I will conclude with a
discussion of the musical results and how this methodology can be applied to
other domains of time-based creation.
2. Motivation and Goals
2.1 Formal
Metaphor and Inspiration
As an
artist working in a time-based medium, I am naturally intrigued by time cycles
that occur in my life and the world around me.
Many composers in particular have utilized this inspiration in their
work. Igor Stravinsky provides a
stunning example in his composition, Symphony
of Psalms [3], which conveys the grandeur of the metaphysical world through
the repetition of musical cycles.
The
motivation and inspiration for my design of this generative model comes from my
experience of watching the play of light against the ocean. In an afternoon on the beach I am drawn to
the trajectory of the sun throughout the day, and the slow progression of
clouds across the sky. Simultaneously,
winds blow across the water, causing ripples and chop on the water, while the
repetition of tidal patterns shift in a meta-rhythm. At the nexus of these intersecting forces is the play of light
against the water; a shimmering surface that is slowly changing in tone and
intensity with the influence of each of these cycles. The particular manifestation of these interacting forces on any
given day is always unique. Nonetheless,
the generative process is always the same.
In
this generative model for the creation of music, I am trying to capture this
essential nature of independent cycles that unfold over different time scales
and contribute to defining a musical surface, that is guided by the underlying
structure. Capturing this sense of flux
and process is a critical musical goal.
2.2
Musical Goals
With this motivation in mind, I have defined two broad musical goals
that I hope the system can achieve.
They are open in that they can accommodate many different surface-level
characteristics, but restrictive to the extent that they define the basis of
music that I hope the generative system will produce.
- I hope to generate large,
slowly evolving forms that are balanced by local variety.
- I hope to generate
musical processes that unfold over time independently for each musical
feature. The surface of the music
is the composite resulting from the interaction of these otherwise
independent processes.
3. The Generative Model
This
generative model for the automated composition of music utilizes a coevolutionary
genetic algorithm [1, 2]. The algorithm
is hierarchically organized, and it is comprised of a population of musical
components including Notes, Gestures, Phrases, Sections, and Metasections.
I
chose to implement a genetic algorithm for this work because the computing
paradigm is sufficiently flexible and open-ended to allow for manipulation and
enhancement to suit the musical purpose.
Additionally, it is possible to leverage features of the genetic algorithm
that are well suited for organizing music.
- An unlimited genetic
feature space can be defined for each member of the population.
- Each genetic feature
evolves independently to yield virtually unlimited combinations.
- Members of the population
will mate with one another to produce children which are a hybrid of the
two parents. For example, two musical Sections can mate to produce a third
Section which will exhibit musical features such as frequency and
amplitude which are drawn from both parents. In this manner, the genetic algorithm affords the
possibility for repetition and distortion in time. This fact allows for the
cross-pollination of salient musical features at various hierarchical
levels.
- A genetic algorithm is a
complex nonlinear system and one cannot predict the outcome of the
evolutionary process without actually running the simulation. Genetic mutation and the infinite
variety of combinatorial possibilities, allow the algorithm to generate
novel and unpredictable results. I want to build a generative system that
is capable of producing musical results that are not explicitly built into
the system and could not have been anticipated. New forms and musical ideas can emerge from the system which
adhere to the goals outlined above, but are not ‘composed’ in a
traditional sense.
3.1 The Evolutionary Process
The genetic algorithm described in this paper does not require any feedback from the author. Unlike selective breeding models [1] that require feedback to steer the evolutionary process, fitness evaluation is accomplished by upper level components within the hierarchical structure.
The population hierarchy and all genetic features are initialized with random variables. The topmost level of the hierarchy does not mate with any peer components, and as a result, the initial seeding of this component will dictate the overall form of the evolved piece. However, all details regarding the fleshing out of this form are determined entirely within the algorithm itself. Each evolved piece of music is unique and I cannot predict nor alter its particular features.
A difficult challenge in any genetic algorithm is to simply determine when the evolutionary process is finished. In this algorithm, through extensive experimentation, I have found that a population will stabilize after several thousand generations. This stability is indicated by a reduction in the percentage of deaths and ill-fit members of the population. Consequently, in most examples discussed in this paper, the evolutionary process is terminated after three thousand generations.
3.2 The Musical Hierarchy
In order to generate musical works which are hierarchically organized and contain feature trajectories that unfold at different timescales, I have implemented a hierarchically organized, coevolutionary genetic algorithm. Metasections, Sections, Phrases, Gestures, and Notes comprise the musical population. In the system, an upper level component, such as a Section, contains a sub population of organisms, such as Phrases. Throughout this paper I will refer to such an upper level component as a ‘parent’ and will refer to its sub components as ‘children.’
A given parent component sets the fitness function for its children, and as these children evolve and change and interact with each generation, they are also redefine the fitness functions for their children. Section 3.4 describes the role of components in different hierarchical levels of the system.
Though the number of tiers in the population architecture is fixed, each population is randomly initialized, and the details of the resulting tree structure are always unique. Figure 3.1 diagrams a possible realization of the hierarchical structure wherein Metasections can contain n levels of other Metasections. At the terminal Metasection level, Metasections contain Sections. Sections contain Phrases, which contain Gestures, which contain Notes. The Note is the fundamental component of the structure.
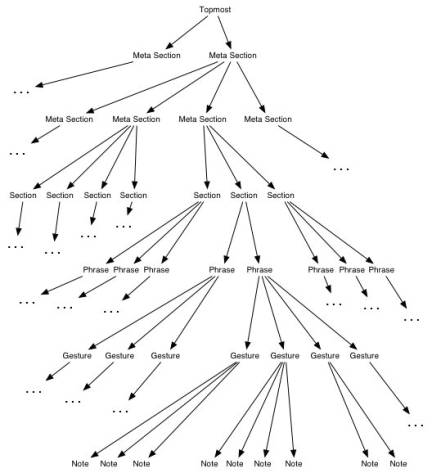
Figure 3.1
3.3 Role of Components in the Hierarchy
3.3.1 Note
The Note is the terminal level of the musical hierarchy. Notes are realized as musical events at the final stage of the generative process.
3.3.2
Mid-Level Components
Mid-level components, including Gestures, Phrases, Sections, and Metasections, are not directly realized as music. Their primary role is to shape the feature trajectories and bandwidths for their child components.
3.3.3 Topmost
Level
The
topmost level of the hierarchy does not mate with any peer components, and as a
result, the initial seeding of this component will dictate the overall form of
the evolved piece. The evolutionary
process leads toward a realization of the global structure that is fixed in the
initialization of the topmost level.
4. Expanded Scope of the Genetic Feature
A given Phrase could evolve a population of Gestures that simply cluster at random around some specified value. However, I want the system to generate groups of components that are organized in such a way that they yield discernable trajectories over time. I want Phrase groupings to emerge that contain groups of Gestures moving from low to high, and returning to a medium level. Similarly, I want a sequence of adjacent Phrases to yield a perceivable progression of feature trajectories with each new Phrase. Consequently, a number of additional dimensions have been added to each genetic feature to facilitate the generation of independent feature trajectories at each level of the hierarchy. Exactly as with the basic genetic values, these additional dimensions are exchanged, mutated, and inherited through the process if reproduction, and as a result, the genetic pool for these additional dimensions is perpetually varying and evolving with each passing generation.
Each genetic feature of a component is defined by this expanded set of dimensions. Some of these dimensions govern the component itself, and some define contours that dictate the relationships between child components. In this section I will describe these additional dimensions and explain how they contribute to the creation of sophisticated feature trajectories.
4.1 Fundamental Dimensions
4.1.1 Primary
Value
The essential dimension of a feature is its primary value. This dimension plays three important roles in the genetic algorithm.
- This feature dimension sets the expressed value of the feature when the component is realized in the generative process. For example, if a Note has an amplitude with a primary value of 0.5, the Note’s amplitude will be set to 0.5 when it is realized by the generative system.
- The primary value dimension is used to evaluate the fitness of a member of the population.
- The primary value is inspected and modified as components interact and organize themselves along the trajectory skeleton defined by their parent.
4.1.2
Bandwidth
Each feature has a bandwidth dimension. This dimension in a parent component governs the range of feature values that its children can exhibit.
The bandwidth is centered around the primary value of a given component. For example, if the primary amplitude value of a component is 0.5 and the bandwidth dimension is set to 0.5, the bandwidth of that feature will span from 0.25 – 0.75. Consequently, any child of this component can have a primary amplitude value from 0.25 – 0.75 and still be well fit along the amplitude axis.
A parent’s bandwidth dimension plays a key role in defining the fitness function for its children. However, the bandwidth dimension does not have a function for Notes, because they are at the terminal level of the population hierarchy.
4.2 Contour Defining Dimensions
The primary role of upper level components in this system is to shape feature contours for their child components. Gestures, Phrases, Sections, and Metasections are not directly realized as sound events, but their genetic features shape the trajectories that drive the music generated by the algorithm. In this section I will describe the genetic feature dimensions that have been implemented to allow the generative system to create musically compelling feature trajectories.
4.2.1 Anchor
Points
In conjunction with the primary value and bandwidth dimensions, four additional feature dimensions frame a skeleton trajectory for a given feature. These dimensions are the start value, middle value, middle value location, and end value. Figures 4.1 a & b illustrate two trajectory skeletons which could be defined by three anchor points.
Squares mark the anchor points of the trajectory, and these points are connected by lines. In Section 5, I will describe how components of the generative system interact with one another to create an infinite variety of lines and curves that flesh out this basic structure.
a) 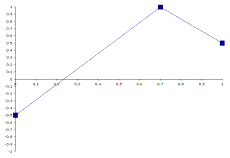 b)
b)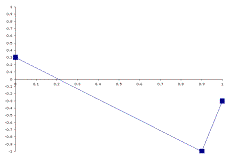
Figure
4.1
4.2.1.1 Start
and End Values
The start and end values define the underlying direction and shape of the feature contour. This feature contour is always centered about the axis of the primary value dimension of the feature. If the start value is less than the end value the overall trajectory of the feature will move from low to high. If the start value is higher, then the overall trajectory will move from low to high. The plots in Figure 4.1 illustrate each condition.
4.2.1.2 Middle
Value
Two feature dimensions, a value and position, define the middle point of the feature contour.
The value of the middle point is a function of the contour direction. This value is derived from subtracting the start value from the end value. As illustrated in Figure 4.1, trajectories which move from low to high, as defined by the start and end values, will have a positive middle direction, while contours that move from high to low will have a negative middle direction. Thus, the middle value is set to either +1.0 or –1.0, but as with all trajectory anchor points, this value is scaled according to the bandwidth dimensions of a genetic feature. This scaling function is described in section 4.2.2.
4.2.1.3 Middle
Value Position
The above method is used to calculate the value of the middle point, but this middle point is not necessarily assigned to the centermost member of a peer group. The middle value position determines the point at which the middle peak of the contour will occur. The middle value position is a percentage that scales across the number of child components contained within the parent to determine which child component will be assigned as the middle value anchor. In figures 4.1a-b, the middle value positions are 0.7 and 0.9 respectively.
4.2.1.4
Assigning and Fixing the Anchor Points
Once the start, end, and middle points have been calculated, they are assigned to the child components of the parent. For example, a Phrase might contain seven Gestures. These Gestures are arranged in ascending order beginning with the Gesture which starts at the earliest time and ending with that Gesture which starts at the latest time. The features of the first and seventh Gestures in this example are assigned by the start and end anchor points. Using the middle value location as a percentage, one of the child Gestures will be assigned the middle value. It is also possible for the middle value position to supplant a start or end point to yield a trajectory defined by only two anchors, a start and end.
In Section 5, I will discuss the process by which adjacent, non-anchor components can organize themselves along the basic trajectory established by these three anchor points. Nonetheless, these three components are rigidly fixed as anchor points, and they will not deviate until the parent’s feature dimensions change.
4.2.2
Bandwidth Scales the Trajectory
In section 4.1.2 I introduced the bandwidth dimension of a genetic feature. In addition to regulating the fitness function for child components, the bandwidth of a given feature scales the trajectory range for its children.
Figures 4.1a-b chart trajectories with peaks at 1.0 and –1.0 that are centered about the axis of a hypothetical primary value. If a given feature’s bandwidth value is 1.0, these full value ranges will be preserved. However, a bandwidth value of 0.5 will scale the trajectory range such that the peaks would reach 0.25 or –0.25. If this trajectory is centered about a primary value of 0.5, the peak anchor point in figure 4.1a, with the same bandwidth value, would reach 0.75, while the peak anchor point of figure 4.1b would dip to 0.25. Bandwidth values which exceed the global 0.0 – 1.0 range are truncated at either bound.
4.4 Bandwidth Contour Dimensions
A feature’s bandwidth value is critical in the organization of feature contours. Given that this dimension plays such an important role in defining the generated forms, I want to provide the generative system with the facility to construct meaningful bandwidth trajectories that unfold over time. This was accomplished through the implementation of an additional array of bandwidth dimensions.
Figure 4.3 illustrates a Phrase, containing four Gestures, which exhibits a gradually diminishing bandwidth trajectory. Using these additional feature dimensions, the genetic algorithm can potentially generate a shape where the first Gesture has a very wide frequency bandwidth that narrows over time before reaching a very narrow width by the fourth Gesture. Concurrently, the amplitude bandwidth might begin very broad and similarly grow narrow by the fourth Gesture. Thus, over the course of this Phrase, the music would start with diverse amplitudes that are spread over a full frequency range, and would gradually focus toward a narrow frequency band at a nearly uniform amplitude level. Such a bandwidth contour would provide a striking musical result that unfolds along with the other independently evolving feature contours for these Gestures.

Figure 4.3
4.3.2 Bandwidth contour dimensions
Just as a component defines the trajectory of primary values of its children, it also defines a contour of bandwidths. Two variables are used for this purpose, bandwidth start value and the bandwidth end value. The bandwidth start value acts as an anchor point and sets the bandwidth for the first child contained within the component. The bandwidth end value sets the bandwidth anchor for the last member. Note that only two points, a beginning and end value, are used to define the bandwidth contour of a component.
4.4 Secondary Trajectory Dimensions
4.4.1
Secondary Trajectory Control
Thus far, I have described the expanded feature dimensions that define feature and bandwidth trajectories for each genetic feature of the system. There is yet another way in which component feature trajectories are organized, secondary trajectory control dimensions. These secondary trajectory dimensions control the trajectory of anchor points for a sequence of child components of a given parent.
Imagine again that a given Metasection contains six Sections. Each of these Sections defines a feature trajectory for each of the Phrases it contains as describe above. While the feature dimensions described thus far are sufficient for generating compelling trajectories within each of the child Phrases in this example, I want to ensure that the trajectories contained within each of the Phrases are not simply repeated. I want the model to generate sequences of musical structures that contain meaningfully shifting trajectories. Consequently, I have implemented an array of additional feature dimensions that define trajectories for the anchor points of child components. These dimensions define starting and ending values for each of the three trajectory anchor points, and are evolved by the genetic algorithm in the same fashion as all feature dimensions described in this paper.
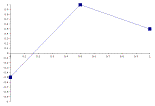
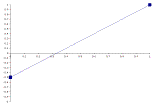
Figure 4.4 illustrates a sequence of trajectories for six Sections in which the middle anchor point moves later and later with each successive component.
1.  2.
2. 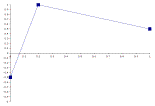 3.
3.
4.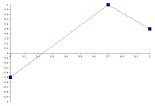 5.
5.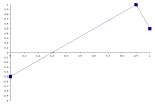 6.
6.
Figure
4.4 – 6 Sequential Sections
With the implementation of secondary trajectory dimensions, a given parent component can set trajectories for the start, end, and middle values of its child components. In the above sequence, only the middle value position is shifted. However, if all three values were to be shifted over a component sequence, the transformation would prove more dramatic. A secondary trajectory could be very small such that a sequence of contours would not change much at all, or the system could generate secondary trajectories where the trajectory is radically transformed over the span of just a few components.
4.4.2 Feature
Dimension Depth Limit
The need for increased variety and control over feature trajectories is mitigated by the fact that this process of deeper and deeper nested levels of control must stop at some point. I have decided to stop at this secondary level. There are no tertiary levels that govern how the secondary levels will change over the duration of a musical component. Furthermore, I did not define additional middle values to act as targets for these secondary control values.
This balance is guided by the feeling that this level of trajectory manipulation and variation yields results that are discernable to listeners. A shifting trajectory as described in Section 4.4.1 defines an arc that a listener can still readily detect. Through experimentation with the system I have determined that the implementation of more levels of control would risk destroying the sense of meaningful progression, and might rather cross into a perceptual realm where feature trajectories seem to be generated at random. This limit on the nesting level ensures that the trajectories defined by a family of peer components will not grow stagnant and preserves a perceptible level of continuity between them.
5. Component Intelligence for Contours
I have described feature dimensions that enable the genetic algorithm to generate a wide variety of skeleton trajectories that can independently steer trajectories for each genetic feature of the system. Figure 5.1 illustrates a potential skeleton trajectory for a given feature of a component.
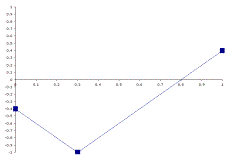
Figure 5.1
Though this basic shape is fundamentally satisfactory, I want the generative system to be able to generate trajectories that include curves and lines that allow for even greater control, variety, and subtlety in the generated forms.
For example, in composing a section of music, I might begin with the notion that the rhythmic activity should move from very still, to a frenetic peak toward the end, suddenly returning to a middle intensity at the end. However, these three points would rarely be linked by a simple linear rise or fall in activity. Rather, an exponential curve might link the first two points, followed by a shallow logarithmic curve between the second two points. Any variety of curves might potentially join two points, and this is a vital formal feature that I want to the system to generate.
In order for the algorithm to generate a great variety of connecting curves I have implemented a system of low-level intelligent interaction between adjacent components so that the organisms themselves can work together to generate compelling feature trajectories.
5.1 Component
Intelligence
In the generative system, complex, curved contours arise from local interactions of intelligent musical components. In addition to the global cycle of life, death, and reproduction that drives the evolutionary process, each component in the hierarchy has an awareness of the state of adjacent members in its peer group. For example, if a Phrase contains nine Gestures arrange in ascending order according to their start times, the first and second Gestures can relate their feature sets to one another. Similarly, the second and third Gestures are aware of one another just as the third and fourth members of this group are aware of each other. This local awareness allows a group of components to fit themselves loosely along the contour skeleton that is defined by their parent.
To illustrate how these local interactions contribute to the construction of feature contours, I will refer to the contour graph in figure 5.1 and assume that nine Gestures are to fit themselves along this amplitude contour defined by their parent Phrase.
As discussed in the previous section, there are three anchor points in this group. The first Gesture of this group, Gesture1, will have its amplitude set to –0.4 (scaled according to the bandwidth of the containing Phrase). The middle Gesture is the third member, Gesture3, and will thus have its amplitude set to –1.0 (also scaled of course). The ninth Gesture, Gesture9, will be anchored at an amplitude value of +0.4. The remaining, non-anchor Gestures use local intelligence to organize themselves along the basic trajectory specified by the parent Phrase. Thus, Gesture2 must position itself somewhere between Gesture1 and Gesture3 to link the first two points. Between Gesture3 and Gesture9, five Gestures must sort themselves along any ascending curve from –1.0 to +0.4. With each generation of the genetic algorithm, each Gesture will make minor adjustments to its features until all nine gestures are sorted into the proper order that fleshes out the underlying skeleton trajectory. The feature distances between adjacent members of this group are not set by the parent Phrase. This low-level, intelligent sorting process yields any variety of curves which could join the three anchor points, and Figures 5.2 a-d illustrate solutions that could result from this component interaction.
a)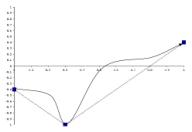 b)
b)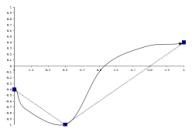
c)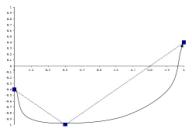 d)
d)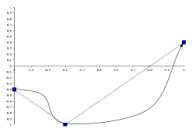
Figure 5.2
Figures 5.2-d illustrate contour shapes that are musically compelling and familiar. Imagine that these contours govern the amplitude shape of a Phrase, or the rhythmic acceleration of a Gesture. Imagine that they shape a fall and rise in frequency over the duration of a long Section, or that they steer a timbral motive across a Phrase.
By evolving a population of intelligent musical structures, the system itself can explore the creation of an infinite variety of feature contours, and thereby generate complex and discernible musical forms.
5.2 Bandwidth
and Secondary Trajectory Intelligence
In previous sections I have described how anchor points for bandwidth and secondary trajectories are used to define contours for bandwidths and skeleton trajectories. Exactly as described for feature contours, local intelligent interactions between adjacent components will generate a great variety of curves to link these bandwidth and secondary trajectory anchor points.
6. Musical Results
The true measure of the success of the generative algorithm is the quality of the music it generates. ‘Quality’ is defined according to adherence to the points described in Section 2. Over the course of working on this project I have been encouraged by the steady improvement in the quality of the resulting music. The first musical outputs were undifferentiated from one another, and exhibited flat trajectories at the formal and local levels. As the feature dimensions were enhanced, more varied trajectories began to emerge. As the feature list was expanded, the generated pieces grew in sophistication and clarity. This improvement in the musical results is evidence of an increased understanding of the critical features of the music I hoped to generate and my ability to quantify their influence.
As the project progressed, I also felt
that as a listener I was increasingly able to navigate the musical structures
that emerged and could more clearly recognize my own musical biases in the
pieces. This ability to grow more
conditioned to the musical style of the genetic algorithm provides further
evidence of the increasing sophistication of the generated music.
Another musical goal of the project was
to generate music that exhibits large-scale, slowly evolving forms and
addresses the passage of time on multiple levels. The genetic algorithm produces pieces that exemplify such forms.
7. Conclusions
The evolutionary framework described in this paper provides an effective means of generating an unlimited number of independent feature trajectories that unfold over time. These trajectories are musically compelling at every level of the hierarchical structure, and they contain sufficient variety and sophistication to support the creation of large-scale musical forms.
7.1 Other
Time-Based Media
This paper describes the implementation of a generative model for the creation of music. Nonetheless, this methodology for using a genetic algorithm to generate independent feature trajectories that unfold over time in a hierarchical structure is applicable to any time-based media.
The genetic features described in this paper are used to drive features such as amplitude trajectories and harmonic progressions. These trajectories could also be mapped to drive video filtering parameters in a generative model for video art. They could drive actuators in a kinetic sculpture, or could shape the environment of an active installation. The generative model is intentionally flexible to allow for extrapolation to other domains.
8. References
[1] Holland, J., Adaptation in Natural and Artificial Systems, University of Michigan, Ann Arbor, 1975.
[2]
Husbands, P., Distributed Coevolutionary Genetic Algorithms for Multi-Criteria
and Multi-Constraint Optimisation. Evolutionary Computing, AISB Workshop 1994:
150-165
[3] Stravinsky, I., Symphony of
Psalms. Boosey and Hawkes, London, rev.
1948.