A molecular collision model
of musical interaction
Peter
Beyls
Hogeschool Gent,
Belgium &
Computer Music Research,
School of Computing, Communications
and Electronics,
University of Plymouth, UK
peter.beyls@plymouth.ac.uk
Abstract
This
paper speculates on the potential of a limited set of interacting particles to
produce interesting temporal structures in a two dimensional world. Particles
exchange information locally though global complex behavior emerges
spontaneously. The imaginary physics of the world is described in an ensemble
of 2D arrays. An autonomous genetic algorithm continuously aims to optimize the
arrays in an effort to maximize diversity. In addition, an external user may
interfere in a subtle way; external gestures are integrated into the arrays in
proportion to their strength. A quite elaborate mapping scheme creates
relationships between complex system behavior and parametric MIDI events.
1. Introduction
The present paper formulates a generative
system featuring native internal dynamics open to disturbance by unpredictable
actions from an external user. It follows the general working hypothesis of
much Alife research; life-like phenomena can be studied by building distributed
systems composed of many interacting components. Complex global behavior
emerges spontaneously from a collection of simple local interactions between
the constituting elements. These elements vary widely in dimension and
character; consider for instance, communicating newsagents living on the
Internet, social forces between people in a given society or molecules engaged
in a chemical reaction. The behavior of such systems cannot be envisaged from a
critical analysis of its components; in particular, the mutual relationships
between components will force a global unpredictable functionality.
In addition, various cognitive abilities have
been characterized as distributed, self-organizing systems (Minsky, 85). The
fluid dynamics approach of (Hofstaedter, 95) suggests the study of cognitive
processes, including creative decision making, as processes of molecular
interaction. Again, coherent structures appear from the random flux of
continuous interactions amongst molecules. Our work adopts the metaphor of
colliding molecules as a first principle and thus also relates to recent work
in artificial chemistry (Dittrich, Ziegler & Banzhaf, 01).
Our
application proposes a model of musical man-machine interaction based on the
real-time interpretation of particles interacting in a closed container. The
container may be either of imagined toroidal shape or feature reflective walls.
The internal physics of the system, i.e. what happens when any two particles
collide, is represented in a 2-dimensional array. The array instructs particles
to move in particular directions. The user interferes with this innate behavior
by modifying the array through physical gestures. The user does not exercise
explicit control but rather disturbs the expression of an otherwise autonomous,
internal physical law. The basic idea here is to synthesize families of waves
of variable coherence and periodicity. The complexity of the waves follows a
law and the user has only limited and indirect instrumental control over the
quality of the wave propagation process.
2. Motivation
The
present experiment grew from earlier work with cellular automata (Beyls, 04).
CA are idealized systems to study complexity in natural and synthetic phenomena
but as models they are discrete both in time and space. However, one could
actually interpret embedded particles in CA as interacting molecules (Hordijk,
Crutchfield & Mitchell, 96). This work interprets domain borders of
space-time diagrams in one-dimensional automata as particles. Still earlier work by Ed Fredkin suggests CA
as models of ballistic computing. The billiard ball model has great musical
potential since its novelty consists in focusing on the detailed evolution in
time of an individual microscopic state – in contrast to studying macroscopic
quantities based on a statistical distribution of states (Toffoli & Margolus,
86). This collision model successfully performs logical operations using
mirrors as routers.
Now,
in an effort to generalize, we may think of particles as responsive objects of
arbitrary complexity and even equip them with some form of long-term memory.
Consider, for instance, people meeting and interacting in a public space.
Social behavioral patterns will surface spontaneously. However, the work
described here takes the atomic route to complexity engineering; the objects we
use feature a single instance variable – the angle of movement -- and cannot
remember former actions (no memory).
Related work
The
discipline of artificial life has spawned many incarnations of distributed
computational models. According to the field of application we speak, for
instance, of particles, molecules, agents or artificial creatures. Particle
systems have a long history in the computer simulation of complex natural
phenomena. They are instructive, early examples of studying complexity by
considering relationships amongst small buildings blocks – in contrast to using
differential equations. More recent work by (Reynolds, 87) describes the
flocking of birds (boids) as an emergent process. The Swarm simulation
environment developed at the Santa Fe Institute (Minar, Burkhart, Langton &
Askenazi 96) is also a significant example.
The
swarm and boids ideas was recently adapted for musical purposes by (Blackwell
& Bentley, 02). Swarmmusic is an interactive music improviser. It maps the
positions of particles/boids to positions in MIDI space. An external human
improviser may act as a temporary target for the swarm. Style-scripts provide
additional parametric control over the nature of the interaction thus further
conditioning the musical output.
Earlier work of the present author has addressed the potential of
real-time man-machine interaction in virtual worlds. Four different agents
oriented systems aimed at interactive composing are documented in (Beyls, 97).
3. Formal definition
For
our purpose, a molecular system is characterized as a tuple {M, R, A}
where M is a finite and fixed size collection of basic molecular
building blocks and R denotes all possible interaction rules. A
specifies an algorithm incorporating additional parameters conditioning how and
when the rule R will be applied. Note that the interaction vessel itself
is assumed to remain fixed, it is of no qualitative concern to a formal
description.
We
consider the density of molecules to be fixed (8 in our implementation) and,
for clarity; we shall modify a molecular feature (the angle) instead of
changing the concentration and/or type of molecules.
The
system activity is formally summarized as:
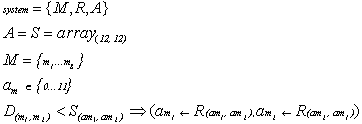
The algorithm A
is equivalent to S, a sensitivity matrix. It holds numerical values
expressing a threshold for interaction between any two types of molecules to
take place.
The
vessel contains 8 molecules defined by M. All molecules move in a
direction defined by their momentary angle. The state space of angles is
discrete and has a resolution of 30 degrees, so relative angles range between 0
and 11 to cover full circle. Note that angles are spread out evenly in that
circle. Note also that the angles resolution has a very strong impact on the
potential temporal complexity of the system as a whole; higher resolution will
expand the state space in an exponential way. (This will be addressed in future
implementations).
Interaction
rules R are also described explicitly as regular arrays of 12 by 12 elements.
The angles of interacting molecules receive specific interpretation. Both
angles are interpreted as to index locations in the array -- to retrieve the
new values of both respective angles. The array is a simple and compact way to
represent how 12 different types of molecules potentially interact. The state
space of all possible matrix rules is huge (12 expt 144 is a 156 digit number!)
and thus considered virtually infinite.
The
effect of the rule array is qualitative control over molecular collisions. Now,
interactions between molecules become effective when their physical distance is
less than their mutual interaction threshold defined by array S. When
interacting, both molecules will update their angle. For clarity, sensitivity
values S are symmetric in the current implementation, though
unequal sensitivity values would certainly add higher degrees of non-linearity
to the system.
4. Implementation
The array
The
above figure shows the systems architecture. The central 2-dimensional array
acts as a lookup-table rule, which molecules in the vessel address. Interacting
molecules modify the vessel as a whole thus conditioning posterior
interactions. This creates a complex dynamical system; a simple simulated
universe is tightly coupled with the expression of a virtual physics defined in
an array. For simplicity, we assume the initial conditions (molecular
positions) to be random. Also note that we are dealing with a non-reversible
system (Prigogine, 84). The future is captured in a deterministic device (the
array) though the global system behavior may appear to feature chaotic
attractors.
Once
set in motion, the couplings between rule array and the vessel -- completely
disconnected from the user -- may orchestrate the sustained synthesis of
interesting waves for hundreds of generations. The array values (0~11) are
mapped to 12 different colors in a private GUI (see fig. 3)
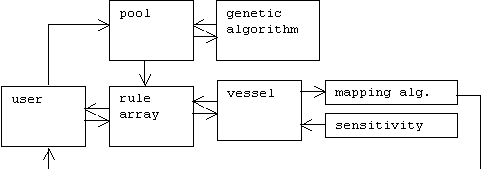
![]()
Fig. 1. Global system architecture.
Observe the two loops incorporating the user.
The user
The
actions of the external user speculate on the possibility to issue qualitative
control over this global behavior albeit in an unusual, indirect way. A user
provides gestures in 2D space; consider MIDI input of a sequence of (pitch,
velocity) events interpreted as a trajectory (x, y) in 2-dimensions. The
current implementation uses mouse input; the user draws some gesture (limited
to maximum 100 coordinate pairs). The gesture is analyzed instantaneously when
a mouse-up event occurs; analysis includes relative length, angularity,
traversed distance, total surface used and acceleration/deceleration. Given a
fixed sampling rate, we obtain information about the character of a gesture,
and consequently, about the motoric personality of a given user.
Now
a gesture modifies the current array plus some of the other arrays in the pool.
The amount of change plus the number of arrays modified is stochastically
proportional to the total length of all segments in a gesture. In addition, the
change in an array is computed following an interpolation algorithm. That is,
the previous contents of an array strays partially into the future. Therefore,
arrays also function as long-term memories.
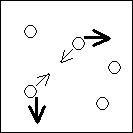
Fig. 2 Prototypical example: two objects interacting according to
their current angle of movement. Thinly drawn arrows denote angles at time
T, thick arrows denote angles at time (T+1).
The vessel
The
simulated vessel is the environment holding molecules moving in a given
direction at constant speed. At every cycle, every molecule checks whether any
other molecule is within its sensitivity range. If positive, the angles of both
objects are viewed as (x,y) pointers in the array. The retrieved value (0~11)
will set the new angle (0~330) of that molecule. In case we are dealing with
asymmetric affinities, some of the neighbor molecules will change their angle
if their sensitivity is high enough. When more than two molecules are within
interaction distance, all neighbors will be evaluated sequentially, the last
value retrieved will finally affect the new angle. The sensitivity between any two angles is expressed in a 12 by 12
sensitivity array. However, most of the experiments reported here use a fixed
sensitivity value for all angular affinities.
The pool
There
is a small critical mass of 8 arrays, one of which is copied into the currently
exploited array. A background algorithm switches continuously between the
arrays when the ‘delta flag’ is true. During every time frame, the specific
array also traces the quality of its performance; it counts the total number of
interactions plus the number of unique instances of angles-histograms
encountered (see Fig 5. History track of angularity histograms). The fitness of
the array will be directly proportional to the diversity in histograms. Arrays
are chosen at random conditioned by the number of times they were chosen
before; the selection probability is inverse proportional to the number of
times used in the past. All arrays are visualized in a graphic user interface
(see fig. 2), small arrays on top are selected by pointing and the two numbers
separated by a colon indicate respectively the nr-times-selected and the
accumulated total fitness.
Fig. 3 Rule array selector and
visual feedback interface. The user implicitly steers a complex dynamical system from the
observation of the cumulative effect of (1) rule array selection and (2)
rule modification, as described above. The user’s evaluation is purely
subjective; one tries to discover relationships between global system
behavior and spontaneous user activity.
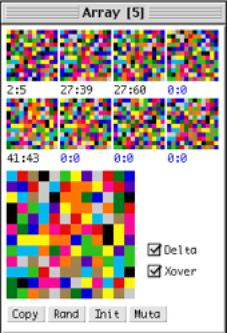
The genetic algorithm
When
the ‘Xover’ flag is set, an autonomous genetic process will act in parallel.
The genetic interpretation and action is straightforward: arrays are viewed as
genotypes subject to standard crossover and mutation operators. The arrays are
first sorted according to fitness, the two fittest are considered parents in
the breeding process yielding 8 fresh arrays. A small amount of mutation helps
prevent premature convergence into a more or less uniform pool.
So
both the user and the GA contribute to the interactive development of
interesting, propagating structures. Actually, a particular type of man-machine
cooperation emerges; the GA clearly aims optimization by creating arrays that
often look quite similar; they converge to some spot in genetic space. On the
other hand, user activity both selects and modifies some arrays, often
profoundly disturbing the GA instantiated structures. The system thus
permanently fluctuates producing patterns of variable regularity. User
initiated actions have two effects; they tend to favor short-term disorder
while also influencing long-term behavior since some of the modified arrays
will survive in the next generation. Machine initiated activity can be
described as background autonomy according to the single criterion of global
system fitness.
The
general advantage of the genetic approach is twofold. First, it allows managing
the external effect of complex processes without fully understanding the
internal machinery orchestrating them. Second, genetic algorithms may generate
constructive material that could not be anticipated by an external observer --
so they function as generators of surprise in an otherwise stable system.
For
musical continuity, we rely exclusively on the arrays. The system as a whole
exhibits a certain inertia; arrays are modified by interpolation and the
genetic activity spawns offsprings that inherit features of their parents as
they were living in the previous generation. In other words, the perceived
melodic continuity is an implicit byproduct of the global systems behavior – it
does not result from any form of melodic memory. Consequently, coherent melodic
form issues from the accumulative forces of explicit physical gesture and
implicit genetic evolution.
5 Mapping procedures
The
mapping process defines an imagined relationship between an abstract pattern
generating system and an evolved, elusive cultural system we call music. It is
the most crucial yet the most difficult component of any generative music
generator. We could view molecules as interacting harmonics articulating some
complex sound, we could view the molecules as controlling a black box sound
synthesis algorithm of arbitrary complexity. However, we shall try to map
system dynamics into a melodic sequence with given tonality. The mapping
process avoids momentary absolute values and favors using the first derivate of
the current situation. In other words, the variable distances between molecules
rather than their position are considered. The mapping proceeds as follows:
(defmethod create-melody-slice
((self cawp))
;; only 1 situation of max 7 events
(clear-events (melody self))
(loop with position-distances =
(position-distances self)
with angle-distances =
(angles-distances self)
with interacting-lists = (mapcar
'interacting-p
(subviews self))
with all-durats = '((4 2 2) (16 8 8)
(2 1 1 2 1 1)
(8 2 2) (8 1 1 1
1))
with durats = (take all-durats
(mod (loop for el
in interacting-lists
sum (length
el)) 5))
with ahist = (angles-histogram self)
with maxv = (apply 'max ahist)
with posmaxv = (position maxv
ahist) ;; 0 to 11
with countv = (count maxv ahist)
;; min/maj
with tonaltype = (if (zerop (mod
(apply '+ ahist) 2)) 0 1)
with scale = (nth (+ posmaxv
tonaltype) 24-scales) ;; global
with st = 0 ;; start-time
with chan = 0 ;; midi channel
with d ;; event duration
initially (format t "~a ~a ~a ~a
~a ~%"
ahist posmaxv countv
tonaltype scale)
for i from 0
for cell in (subviews self)
for interact in interacting-lists
for p in position-distances
for a in angle-distances do ;; a is
signed
(setq d (/ (take durats (+ a i)) 10))
(setq chan (if (< p 100) 0 1))
(when interact ;; length of list > 0
(cm::insert-object ;; insert timed midi event
(cm::new
cm::midi
cm::time st
cm::keynum (+ 36
(*
12 (round (/ (point-v (view-position cell)) 40))) ;; octave
a) ;; angle
cm::amplitude (if (plusp a)
(+ 100 (random 20))
(+ 60 (random 20)))
cm::duration d
cm::channel chan)
(melody self)))
(unless (< p 100) (incf st d)))) ;; conditional chord
The
method create-melody-slice, sent to a CAWP object (acronym for continuous
automaton wave propagation), creates consecutive short melodic sequences.
The physical configuration of the cells is significant, though we avoid reading
and interpreting the structural pattern as if it were a conventional musical
score. Note we are dealing with two different but parallel timing processes.
The first one concerns the internal clock controlling the timing of the simulation
including the real-time visualization. Timing is set by the user -- up to about
10 updates per second. The second process handles MIDI events at a much slower
pace; both processes are concurrent though not synchronized. The melody object
sends a message when it has finished playing its current contents, this
triggers the create-melody-slice method and this process repeats
indefinitely. One could say that the mapping procedure occasionally samples the
current situation of a virtual world. The (dis)similarity of the melodic output
will thus reflect how much the world changes from one generation to the next.
Let’s address the mapping algorithm in detail.
The
position-distances and angle-distances are the first derivate of
the respective instance variables, angle-distances are signed values. Interacting-lists
holds a list of all the current neighbors of every cell, if any.
All-durats is a local library of relative duration units, a short
stylistic ensemble of building blocks to be exploited by the algorithm. Durats
is the selected element from that library; the selection pointer equals the
total sum of all neighbors of all cells, modulo 5 (i.e. number of sublists in
all-durats). The local variable ahist is the current angles-histogram,
12 elements wide of which Maxv holds the angle that is most expressed in
the current situation and posmaxv is the position 0~11 of that value in
the histogram. Countv is the number of times the maxv value
occurs in the histogram, it says a lot about how specific that value is and, in
addition, it is a hint to the diversity of the histogram.
Our
system is built inside a larger framework for musical experimentation (written
in Lisp -- Digitool MCL 4.2) that provides many resident composition, pattern
processing and analysis tools, including tonality libraries of arbitrary
complexity. However, the current implementation builds on Western tonality and
uses a simple global variable 24scales holding all major and minor
scales in all pitch-classes. These libraries are precomputed for computational
efficiency. The algorithm decides on major tonality if the sum of all values in
the current histogram (modulo 2) is even, else it is minor. A specific scale is
then retrieved from the scale library using a combined influence of pitch-class
(set by posmaxv -- very
conveniently in the range 0~11) and tonality.
The
algorithm now loops through the various lists; the position-distances are
considered at a threshold of 100, a value derived by trial and error. For
instance, if the distance between two consecutive cells is less than 100
pixels, MIDI events will sound on channel 1 (a value of zero in the program)
else on channel 2. In addition, the
same mechanism exercises a grouping of events, controlling the start-time of
new MIDI events. Thus, chords are always sounding on channel 1.
Finally,
a new MIDI event is instantiated on the condition that the cell under
consideration is actually interacting, if not, a rest is implicitly generated.
The pitch of the event combines 2 forces: octave position follows the vertical
position of the cell and the signed angle value adds an interval (-11 to +11)
to derive the final pitch. The sign of the current angle-distance conditions the
loudness of new events.

The
figure above shows a short score excerpt of a typical molecular interaction
sequence. The global, uniform sensitivity in this example is 15 pixels. We
notice the complex interlocking of rhythmical patterns. A point attractor is
passed through starting at measure 15. The expressive qualities follow
exclusively from the interpretation of a small group of objects moving in 2D
space.
6. Experimental results
The
complexity of the temporal patterns varies widely; given fixed and uniform
sensitivity, it is directly proportional to (1) the number of different angles
at any moment in time and (2) the number of cells that change value at every
cycle.
Our model is
considered a tool to experiment with interesting temporal changes – not so much
to help construct artifacts with a given finality. We focus on qualitative
descriptors such as stability, diversity, sensitivity and relational affinity.
Our model is built as a synthetic world with private physics, an imagined micro
society. Most important, it expresses non-linear relationships between its
components. This implies coherent yet unpredictable behavior; minute external
disturbances can indeed entail massive consequences. From the work of
[Prigogine & Stengers, 84] we know that order can arise spontaneously out
of disorder through the process of self-organization. This principle is scale
invariant, it holds for ant societies as well as galaxies – we shall bring it
into play it in terms of an abstract social system.
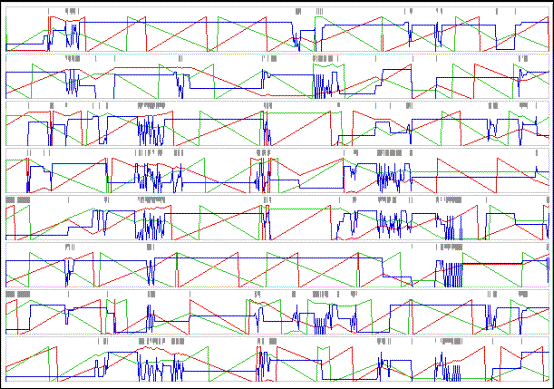
Fig. 4. History track of physical
position and direction
Our
experiments prove that social constructions occur spontaneously. For instance,
given the right initial conditions and the right rule array, a few cells will
cluster and move as a group, incidentally, similar to gliders in a 2D cellular
automaton. At every process cycle, the net effect of all cells executing a
private rule will be a coherent cluster of cells moving in a single direction.
Now, a cell approaching the cluster may interact with its closest component and
implicitly reconfigure the previous social construction. In other words,
collective cycle attractor behavior is destroyed temporarily. According to the
rule, communicating particles may simply bounce symmetrically, act as a
catalyser in a group reaction or engage in circular motion… Many complex
temporal patterns emerge that could be described formally using the notion of temporal
profiles. A profile would capture the rule and the initial conditions and
would then consider the cell’s trajectories and perhaps interpret them as a
collection of tightly coupled breakpoint-envelopes. These envelopes could very
well control a Fourier synthesizer, the result would be the expression of
social control amongst harmonics. This idea awaits further implementation.
Figure
4 documents 600 cycles of an interaction process with 8 molecules in a
container without reflecting walls. A single random rule matrix is used. The
sensitivity matrix holds random values in the range 1 to 30. There is no
gestural input from the user, so the internal dynamics develop in isolation, as
a closed system. Green and red lines respectively denote x and y coordinates and
blue lines show the momentary angles. The gray patches indicate when a
particular molecule is actually engaged in interaction. The gray patches at the
top of each graphic pane make it possible to detect chain reactions.
Qualitative oscillations of angle values are clearly observed. So there is
evidence that this type of complex dynamical systems may support modeling wave
propagation. According to the contents of the rule array, the waves may either
sustain or lead to a single angle value, the latter being equivalent to point
attractor behavior.

Fig 5. History track of angularity
histograms.
Figure
5 shows 12 data tracks in time, 600 generations long, each track represents an
angle from 0 to 330 in steps of 30 degrees. Angle histograms are computed at
the end of every process cycle; this provides information of which angle values
are in use, reflected in the density of the track (1) in addition to how many
instances (2) of these angles are being used, reflected in the thickness of the
track. The sensitivity array is uniformly filled with a fixed value of 15,
which means a global sensitivity value of 15 pixels.
A
subtle user gesture at around generation 400 slightly modifies the current rule
and forces a new type of waves to appear. First, past behavior is gradually
acknowledged and second, amplitude and periodicity gradually build up towards a
regular pattern. After a few generations, the internal dynamics will modulate
that pattern and it will evolve according to the nature of the modified rule.
One could say this constitutes a second kind of macroscopic behavior; waves
appear to interact as bigger constellations; in effect, a neat example of
emergent behavior.
7. Conclusion and outlook
This
paper documents early experiments with an object oriented collision model
supporting musical experimentation in real-time. It can be considered a
continuous cellular automaton, a form of ballistic computing or an example of
artificial chemistry. Anyway, the key notion here is emergence.
Interesting temporal structures appear from the expression of a simple rule
captured in a 2D array. These structures are thought of as propagating waves.
The role of the user is quite subtle; one does not tweak a series of black-box
global variables, in contrast, one shares forces with a genetic algorithm
acting in parallel. So implicit autonomous actions as well as explicit user
activity steer the relationships of an ensemble of objects moving in a 2D
virtual world. Imagine a virtual physics of which the expression and evolution
is partially controlled by an external user.
The
system acts successfully as a generator of interesting waves of variable
periodicity, even when operating according to the following constraints:
(1)
a fixed and uniform sensitivity range for all cells,
(2)
a fixed step size for all cells
(3)
a fixed density and energy of cells,
(4)
a discrete and small set of potential actions i.e. only angles change
(5)
no changes introduced by angle inversion when bouncing a reflective
wall, and
(6)
genetic background activity is switched off.
It
proves that the economy of expressing simple angular relationships in an array
does indeed suffice to support interesting, non-linear dynamic behavior.
However, further work is needed to classify families of automata and to study
the impact of initial conditions. Automatic classification could even be
addressed in an unsupervised offline algorithm since complexity criteria are
explicitly available.
The
work documented here is implemented in Macintosh Common Lisp using the
functionality of the MIDI drivers in Common Music (Taube, 97). Our
implementation challenges Lisp for real-time work. No doubt, Lisp is the most
powerful symbolic programming language yet it has trouble coping with the
pressure of real-time control – to the best of our knowledge, just one effort
aims to connect the universal power of Lisp with the optimized number crunching
efficiency of Max/MSP [Garton]. More work is needed to design robust
multi-purpose, concurrent computational environments using symbolic programming
languages.
References
Dittrich, Ziegler & Banzhaf. Artificial
chemistries, A review. Dittrich, Ziegler & Banzhaf. 2001
Beyls,
P A survey of agents based real-time interactive systems. Proceedings of
the ICMC97, Thessaloniki, ICMA, San Francisco, CA, 1997
Beyls,
P Cellular automata mapping procedures. Proceedings of the ICMC04,
Miami, ICMA, San Francisco, CA, 2004
Blackwell,P
& Bentley,P.Improvised Music with Swarms, Proceedings
of Congress on Evolutionary Computation 2002. [BLBEC2]
Minar, N,
Burkhart, R, Langton, C. and Askenazi, M, The Swarm Simulation System: A
Toolkit for Building Multi-Agent Simulations SFI Working Paper nr.
96-06-042, 1996
Minsky, M. The society of mind,
Simon and Schuster, NY 1985
Toffoli, T. & Margolus, N. Cellular
Automata Machines, MIT Press, 1987
Prigogine, I. & Stengers, I Order
out of chaos, Bantam Books Inc 1984
Hordijk,
W. Crutchfield, JP & Mitchell, M Embedded particle computation in
evolved cellular automata, PhysComp96, New England Systems Institute, 1996
Garton,
B. Maxlisp encapsulates CLISP within the Max/MSP
real-time music environment. See: http://music.columbia.edu/~brad/maxlisp/
Reynolds, C. Flocks,
Herds, and Schools: A Distributed Behavioral Model Computer Graphics
(Proceedings of SIGGRAPH ’87) 21: 25-34. 1987
Taube, H. An introduction to
Common Music, Computer Music Journal, Vol 21, nr. 1, 1997