Topological Approximations for
Spatial Representations
P. Coates AA Dipl, C. Derix MSc
DiplArch, T. Lau MSc BScArch,
T. Parvin MSc DiplArch and R.
Puusepp, MSc MArch
Centre for Evolutionary Computing in Architecture
School of Architecture and Visual Arts, University
of East London, London, UK
e-mail: p.s.coates@uel.ac.uk + c.derix@uel.ac.uk
Marshall McLuhan once
said in his book Understanding Media that ‘Environments
are invisible. Their ground rules evade easy perception.’ Evasive
perception leads to fuzzy representations as shown through Kevin Lynch’s mental
maps and the Situationists’ psycho-geographies. Eventually, spatial
representations have to be described through abstractions based on some
embedded rules of environmental interaction. These rules and methods of
abstraction serve to understand cognition of space.
The Centre for
Evolutionary Computing in Architecture (CECA) at the University of East London has
focused for the last 5 years on methods of cognitive spatial descriptions,
based largely on either behavioural patterns (i.e., Miranda 2000 or Raafat
2004) or topological machines (i.e., Derix 2001, Ireland 2002 or Benoudjit 2004). The former being agent based, the latter
(neural) network based.
This year’s selection of
student work constitutes a combination of cognitive agents + perceptive
networks, and comprises three theses:
Tahmina Parvin (section 1, p.2):
an attempt to apply a Growing Neural Gas
algorithm (GNG) - an extension of the traditional Kohonen SOM (self-organizing
feature map) - to spatial representation. This follows as a direct consequence
from previous work (Derix 2001 and Benoudjit 2004) where the rigidity of the
simple SOM topology during learning became problematic for representation.
Renee Puusepp (section 2, p.10):
an experiment to create a genuinely intelligent agent to synthesize perception. This work also uses the connectionist model
as a basis for weighted learning. Agents learn to direct themselves through
environments by distinguishing features over time using a type of weighted
behavioural memory.
Timothy Lau (section 3, p.16):
a route finding method as outcome
from an ant-colony algorithm constraint through way-finding operations and an
environmentally generated topology. This work was stipulated by ‘live’
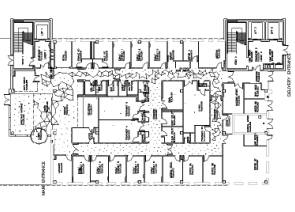
architectural briefs to solve health-care lay-outs.
All three projects are in
development and promise to be explored further. Their relevance cannot be
underestimated at a time when so called ‘smart’ technologies seem to have been
exploited and the demand for self-regulating ‘intelligent’ media is growing.
This means for architects that they will need to understand the occupants’
perception and their behaviours in more depth by using such simulation methods
like the ones presented below:
+
section 1 +
GROWING NEURAL GAS.
SELF-ORGANIZING
TOPOLOGIES FOR SPATIAL DESCRIPTION
Abstract
Space can cognise itself
from elements of social system and can be self-generative at the same time.
Architectural space can be visualized as an autonomous, adaptive and intelligent-complex
system coupled with other autonomous complex system. Adaptive behaviour of
autonomous artificial system of growing neural gas is exploited as a model of
cognitive process for built environment. Cognition can be defined in terms of
ability to respond to the environmental events, and the ‘stimulus’ is the part
of environment that is absorbed by the structure of the model. Space can be
expanded, deformed, fragmented, decayed and above all self-organized by
learning from constituent of environment.
Programs or events can be
constructed by combination of actions and can be represented as point intensity
on probability space. Space is constructed by intentional actions of
individuals. Growing neural gas can be viewed as a ‘distributed representation technique for the spatial description’
of space, can learn and adapt itself according to point intensity on space.
Different space – time
conditions can create topological displacement and variation in spatial
character.
In general, the
discussion is about the morphology of growing neural gas as an artificial
autopoietic system and how it can couple to relevant features of the
environment, as a two-way learning mechanism. The model’s synergetic
construction of topology is a mental construction towards a theory of space.
Space can be viewed as open, complex and
self-organizing system, which exhibits phenomena of non-linearity and
phase-transition.
The notion of spatial
cognition
Spatiality refers to mental
perception of space, mapping environment and behaviour.
Spatial analysis is about the
interrelationships between behaviour and properties of the man-made
environment. It is about the techniques that objectively describe environments.
This description can be related to specific local level phenomena of human
behaviour such as vision, movement, perception, action or particular global
phenomena of complex system.
Cognition or
‘knowing’ is the perception of environmental change. It is the design process
in nature and artificially intelligent system. Pointed out by Herbert Simon, any
entity, be it natural or artificial, that devises courses of action
aimed at changing existing situations into preferred ones (whatever they
might be), can be said to engage in
design activity [Simon, 1981].
Cognition
can be modelled
as the embodied, evolving, and interaction of a self-organizing system with its
environment as a design process in nature. Time-dependent cognition is an
essential component of life or artificial life. All living systems or
artificially living systems are cognitive systems. Cognition is simply the
process of maintaining itself by acting in the environment.
Maturana and
Varela define 'cognition' in terms of basic ability to respond to environmental
events. Design is a cognitive activity that all humans, other living beings,
and the intelligent machines, are engaged in. The nature of design activity is
highly diversified, as the underlying cognitive processes involved in different
domains are fundamentally different.
Space is a container, and action is what we do within it. A kind of natural geometry is generated by actions and movements on space. As an example, a group collectively define a space in which people can see each other, mathematician defines it as ‘convexity of space’, and represents it by points on space.
Formal and
spatial aspects of architectural and urban design are known as
‘configurational’ research techniques, which can easily be turned round and can
be used to support experimentation and simulation in design. This way is one
kind of attempt to subject ‘the pattern aspect of elements in architecture’ to
rational analysis, and to test the analysis by embodying them in real designs.
Spatial
scales can be local and global. The local scale deals with immediate neighbours
and global scale deals with overall spatial configuration.
Graph-based topological
model in archiectural spatial analysis
Graph-based operationalizations of space, which are used for mental representations of environment in the field of architecture and cognitive science, describe environment by means of nodes and edges, roughly represent to spaces and their spatial relations. Edges implement relationship between nodes. Graph-based model is flexible, extendable, and its’ generic framework with straightforward algorithms help to solve specific higher-level questions regarding architectural spatial issues.
Mental representations of space cannot be seen independently from the formal and configerational properties of the corresponding environments. At the same time, formal description of a space as used in architecture gain rationality by incorporating results from cognitive research, which give the prediction and explanation of actual behaviour of the system. Graph- based diagrammatic analysis deals with theory of space gives quantitative expression to ‘elusive pattern aspect’ of architectural and urban design. It is a ‘neutral techniques’ for the description and analysis of the ‘non-discursive’ aspects of space and form. Graph based models are used for quantitative comparisons between spatial configurations in order to identify the essential properties in terms of function or usage. It is considered as strictly formalized description system of space. Beside applied research, graph investigations in architecture particularly concentrated on methodological issues such as the analysis techniques on arbitrarily shaped environments on variable scale levels and on the formalization and automation of the graph generation process within certain complex spatial system.Turner, Dexa, O’Sullivan, & Penn (2001) have proposed visibility graphs in different way to optimise the computational graph analysis. Visibility graphs replace the isovist as node content by inter-visibility information translated into edges to other nodes. Visibility graphs are useful to predict spatial behaviour and affective qualities of indoor spaces.
Neural networks and graph-based topological representation
Knowledge is
acquired by the network from its environment through a learning process and
Interneuron connection strengths are used to represent the acquired knowledge. The every single unit
could be the metaphoric representation of an individual entity and lines could
be communication links. A neural network can be represented as a graph
consisting of nodes with interconnecting synaptic and activation links.
Self-organizing neural network: Growing Neural Gas
Self
–organizing neural network models were first proposed by Willshaw & vonder
Mlalsburg (1976) and Kohonen (1982). The networks generate mappings from
high-dimensional signal spaces to lower dimensional topological structures.
The
“growing neural gas” algorithm of Martinetz & Schulten (1994) seems to
produce compact networks, which preserve the neighbourhood relations extremely
well. The network has a flexible as well as compact structure, a variable
number of elements, and a K-dimensional topology. The algorithm is considered
as spetio-temporal Event Mapping (STEM) architecture. It can be viewed as
decentralized model of human brain learning process or decentralized model of
cognition.
Martinetz
(1994) introduced a class of Topology Representing Networks (TRN), which
belongs to Dynamic Cell Structures (DCS), build perfectly topology
preserving feature map. DCS idea applied to the Growing Cell Structure
algorithm (Fritzke 93) is a more efficient and elegant algorithm than
conventional models on similar task. Growing Neural Gas (GNG) is a class
of Growing Cell Structure. It differs from Growing Cell Structure through its
less rigid topological definition.
GNG only uses
the parameters that are constant in time. It employs a modified Kohonen
Learning rule (unsupervised) combine with competitive Hebbian learning. The
kohonen type learning rule serves to adjust the synaptic weight vectors and
Hebbian learning establishes a dynamic lateral connection structure between the
units. The new model of growing neural gas can be said the extension of
Kohonen’s feature map with respect to various important criteria (Fritzke,
1993a).
Two basic differences with Kohonen SOM:
1 The
adaptation strength is constant over time. Specifically used constant
adaptation parameters e_b and e_n for
the best matching unit and the neighbouring cells, respectively.
2 Only the
best-matching unit and its direct topological neighbours are adapted.
Neural gas as a connectionist model (Donald Hebb 1949)
Brain
operation can be modelled by means of a network of interconnected nodes. Each
Node takes the sum of its inputs and generates an output. The output is
determined by the transfer function of the node, which has to be non-linear.
The connection (synapse) between any two nodes has certain ‘weight’. The
information flows only in one direction. Complex behaviour emerges from the
interaction between many simple processors that respond in a non-linear way to
local information.
The
characters of connectionist models are:
1 High level of interconnectivity
2 Recurrence
3 Distributedness (described
algorithmically)
sparsely connected fully
connected richly connected
GNG
connectionist model consists of a large number of units, richly interconnected
with feedback loops, but responding only to local information.
The process of autopoiesis
An answer
lies in the pattern characteristic of all living systems is autopoiesis, a
network pattern in which each node is a production process that produces or
transforms other nodes. The entire network continually produces itself. The
pattern & process of interaction are called autopoiesis & cognition.
Thus, autopoiesis is the pattern by which life emerges in dissipative systems
and cognition is the very process of life itself.
Virtually autopoietic system can be understood in terms of networks or systems with very simple rules of interaction. These simple rules can lead towards immensely complex sequences. Networks are systems composed of interconnected parts. Relationships between parts are circular (closed loop). This causes feedback because the actions of each component "feeds back" on itself. Both positive and negative feedback is possible.
Autopoiesis generates a structural coupling with the environment: the structure of the artificial system generates patterns of activity that are triggered by perturbations from the environment and that contribute to the continuing autopoiesis of the system. Maturana argues that the relation with the environment moulds the "configuration" of a cognitive system. Autopoiesis is the process by which an organism continuously re-organizes its own structure. Adaptation consists in regenerating the organism's structure so that its relationship to the environment remains constant. An organism is therefore a structure capable to respond to the environment. Autopoiesis is a self-generating, self-bounded and self-perpetuating process.
Growing neural gas as a autopoietic
representation of space
Growing
Neural Gas can be an advance tool for visualization
of emergent spatio-temporal correlations between different entities on space.
The point intensity of signal space can represent activity intensity on a three
dimensional space. More program intensity will generate more signals on space,
which means more stimuli to enhance the system operation.

Self-organizing growing neural gas
Model
description
Current
work
Initially,
the model is an unsupervised self-organizing growing neural gas algorithm. It
has some randomly moving points on three dimensional spaces, which are denoting
the signal intensity on the space. The signals movements are based on Brownian
motion.
The network
start with more than three units ( k > 3), that means with connecting edges
it forms a hyper tetrahedron, which ultimately lead towards k-dimensional
simplex.



k-dimensional
simplex
At first the system
shows a chaotic way of growth and decay and topological displacement. But after
a certain period of time, after it has reached to the maximum growth level,
self-organized itself within the three-dimensional signal-space. It gives a
topology preserving networks of nodes. In this self-organization, every unit
deals with its compact perceptive field with its’ nearest neighbours, which
ultimately gave a compact volumetric topological expression of the space.
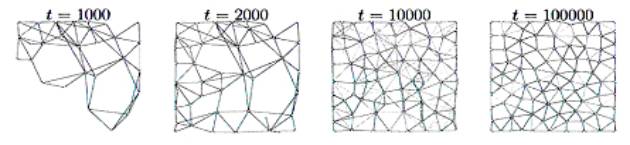



GNG Topologies after thousands iterations
Projected work
Further work
will combine the GNG with a supervised Radial Basis function (RBF) which will
give more potential flexibility to the model and to the clustering of
elements.
Otherwise, the
Ant-based clustering algorithm and growing neural gas networks can be combined
to produce an unsupervised classification algorithm that can exploit the
strengths of both techniques and can be more flexible to describe autopoietic
space. The ant-based clustering algorithm detects existing classes on a
training data set, and at the same time, trains growing neural gas networks.


GNG
with Radial Basis Function
In later
stages, these networks are used to classify previously unseen input vectors
into the classes detected by the ant-based algorithm. The advantage of this
model above GNG model is that the dimensions of the environment don’t need to
be changed when dealing with large databases.
CONCLUSION
In this discussion, the
goal was to establish self generating growing neural gas as an tool to
visualize autopoietic complexity of architectural and urban space. The model is
exceptional for its’ growth process through cognition, the occasional death of
units and self-generation; all of which belong to the core concept of life. The
initial model is a simplest form of growing neural gas model and an abstract
representation of design space.
REFERENCES
[1] Coates P.,
Derix C., Appels T. and Simon C, Dust,
Plates & Blobs, Centre for Environment and Computing in Architecture
CECA, Generative Art 2001 Conference, Milan 2001
[2] Derix C.,
Building a Synthetic Cognizer, Design
Computational Cognition 2004 Conference, MIT, Boston, USA, 2004
[3] Cilliers,
Paul. ‘Complexity and Postmodernism, Understanding Complex systems.’
[4] Bill
Hillier, ‘Space is the machine’, Cambridge University Press, Cambridge, 1996
[5] Luhmann,
N. ‘ The Autopoiesis of social system’, 1972
[6] Maturana
H. & Varela, F. (1980) Autopoesis and cognition: The realization of the
living.
[7] Yehuda E.
Kaley, Architectures New Media. Principle, Theory, and Methods of Computer-Aided
Design
[8] Lionel
March and Philip Steadman, ‘The geometry of environment’. An introduction to
spatial organization in design, RIBA, 1971
[9] Teklenburg,
Jan A.F., Zacharias, John, Heitor, Teresa V. ‘Spatial analysis in
environment-behaviour studies: Topics and
trends’, 1996
[10] Turner
A., O’Sullivan D., Penn A., Doxa M, ‘From isovists to visibility graphs: a methodology
for the analysis of architectural
space’.
[11] Gerald
Franz, Hanspeter A. Mallot, & Jan M. Wiener. ‘Graph-based models of space
in architecture and cognitive science-a Comparative analyses’.
[12] Peponis,
John, Karadima Chryssoula, Bafna Sonit. ‘On the formulation of spatial meaning
in architectural design’.
[13] Fritzke,
B “ Unsupervised Ontogenic Network”, Handbook of neural Computation, 1997
[14] Gerald
Tesauro, David Touretzky, Todd Leen. ‘Advances in neural information processing
system’. MIT press,Vol. 7, 1995
[15] Andrew,
Adamatzky. ‘Computing in Nonlinear Media and Automata Collectives’. 2001
[16] Stephen
Judd, ‘Neural Network Design and the Complexity of Learning.’ MIT Press, 1990
[17] Fritzke,
B. ‘Fast learning with incremental RBF networks’. Neural Processing Letters,
1994
[18] Fritzke, B. A growing neural gas network
learns topologies. 1995
[19] Fritzke,
B. Growing Cell Structures – A self-organizing Network for Unsupervised and
Supervised Learning, 1993
[20] Gerald
Tesauro, David Touretzky, Todd Leen. ‘ A growing neural gas network learns
topologies’. ‘Advances in neural information processing system’. MIT press,Vol.
7, 1995
[21] Martinetz and Schulten, A “neural-gas”
network learns topologies, 1991
[22]
Martinetz and Schulten, ‘Topology representing networks’, 1994
[23] Jim
Holmtrom,‘Growing Neural Gas’. Experiments with GNG, GNG with Utility and
Supervised GNG
[24] J.
Handl, J. Knowles and M. Dorigo, ‘Ant-based clustering: a comparative study of
its relative performance with respect to k-means, average link and 1d-som’.
[25] Conroy,
Ruth. ‘Spatial Intelligibility & Design of VEs’
[26]
Toussaint, Marc. ‘ Learning maps for planning’
[27] X. Cao,
P.N. Suganthan, Video shot motion characterization based on hierarchical
overlapped growing neural gas networks
[28] Randall
D. Beer, ‘Autopoiesis and Cognition in The Game of Life’.
[29]
Gershenson, Carlos. Francis Heylighen.‘How can we think the complex?’
[30] Wendy X.
Wu , Werner Dubitzky. ‘Discovering Relevant Knowledge for Clustering Through
Incremental Growing Cell Structures’.
[31] K.A.J.
Doherty, R.g. Adams, N. Davey. Hierarchical Growing Neural Gas
[32]
http://www.neuroinformatik.ruhr-uni-bochum.de_
/ini/VDM/research/gsn/DemoGNG/GNG.html
+
section 2 +
Synthetic perception. Processing spatial
environments
Abstract
The way we perceive the environment around us is
inseparable from our decision-making and spatial behaviour. Learning to find
one’s way around in a foreign city does not rely only on one’s cognitive
skills, but it is also dependent on the clarity of urban layout. Computational
models have proven to be highly useful in simulating various aspects of
sensory-motor conduct, and help to explore the fundamental principles of
environmental behaviour. The proposed paper employs algorithms to assess
intelligibility of spatial arrangements, and suitability of these algorithms to
elucidate the processes of cognitive mapping. During the exploration of digital
models, semi-autonomous agents develop a set of formal rules to interact with
the environment.
Introduction
Architectural
space is full of cues. These cues, either intentionally designed or randomly
established, determine the way people use the space. If features of space
happen to give misguiding signals, space becomes inefficiently used. One can
argue that environment has some sort of intelligence that communicates with its
inhabitants; one can even claim that people are capable of magnifying this
intelligence. There can be a certain kind of embedded intelligence in the
environment – an intelligence that makes the environment literally speak or
automatically adjust itself. However, speaking of traditional urban
environment, there can be only embedded intelligibility. The intelligibility of
space determines the capability of being understood by an intelligent
inhabitant. In other words, the space does not contain any self-explanatory
information per se; it is the observer who carries the meaning with him.
From that point of view, the space is unconscious medium like a piece of paper.
Merleau-Pointy [1] sees intelligible space as an explicit expression of
oriented space that looses it meaning without the latter.
Spatial
behaviour is very much affected by one’s knowledge of the space and vice versa.
The perception of space is never static but evolves over time. Perception is
locked in a reciprocal dialogue with the movement of the inhabitant. The way
the environment coerces us to move, can be more or less in conflict with our
natural movement, which is defined by the proportions of our body and by the
speed of the locomotion.
An organism’s
ability to learn is strongly related to its position in the evolutional
timeline. Higher organisms have less intrinsic behavioural patterns, and depend
more on their experience. Environmental learning involves obtaining appropriate
sensory-motor conduct, and storing spatial information for future use. In
literature, such stored environmental data structures have been referred as
cognitive maps [2] and environmental images [3].
This paper
considers cognitive mapping – also known as mental mapping – as a method to
collect, restore and retrieve environmental information. Maps are
representations of the environment, acquired through direct or mediated
perception. Psychologists and geographers have used the term ‘cognitive map’
for decades in context of way-finding and environmental behaviour [4].
The cognitive
map possesses a kind of continuity; a certain procedural or algorithmic
sequence that we follow in order to get from one point to another. The map is
more a routine-like description, a behavioural description of an environment
rather than a structural description of surroundings. From architects’ and city
planners’ point of view, it is worth studying the process of cognitive mapping
and its major shapers, because it could reveal the fundamental principles
behind environmental decisions.
Artificial
perception of space
This paper
explores a contingent way to approach processes of cognitive mapping using
computational methods. It is impossible to explain the full range of natural
cognitive mapping with computational models, but these models still provide
some helpful insights. The usefulness of these maps is best displayed in
unravelling wayfinding difficulties within multi-agent environment. The
proposed algorithm tries to exhibit essential parts of cognitive mappings such
as collecting, storing, arranging, editing and retrieving environmental data.
Flow of the algorithm
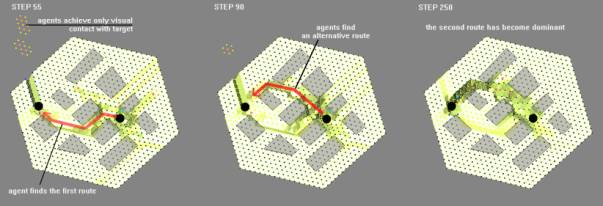
The algorithm under
review benefits from several well-known concepts. The goal of the agents is to
find a way to an assigned target point while interpreting sensory input and
leaving some trails into the environment. Successful agents are awarded by
upgrading their value; the value of a non-successful agent is reduced to
minimum.
Agents are using a
combination of computational cognitive map, which is agent’s
representation of the environment, and syntactic instructions that determine
how that map is interpreted. An agent is ‘born’ tabula rasa – the
evolution of the map and the reference to it happens during its interaction
with the environment. Conception and fade-out of cognitive data is simulated
using pheromone trail algorithm – last visited spots contain more information
than formerly visited ones. Syntactic instructions have to develop and change
according to this dynamic environment. The pursuit of targets is facilitated by
trivial vision. If the visibility line between the agent and its target is
clear, the agent takes an automatic step towards the goal.
Besides
individual learning, the development of an agents’ syntactical instructions
also takes place at a phylogenetic level. Evolution of agents is similar to
evolution of Braitenberg’s vehicle type 6 [5]. A single agent is chosen for
reproduction. However, in the process of reproduction only 75% of syntactical
instructions of the agent have been transmitted to its offspring. The
selection of the parent agent is partly up to chance – the best (by
value – see above) of a subset of randomly selected individuals gets the honour
to be copied. 
1. Input-output
coupling. Agent
obtains input from digital environment and from the cognitive map.
Output is generated interpreting input according to syntactical rules
(reference of the cognitive map).
Design of the agent
The design of
the agent is fairly simple. The visible entity of the agent consists of the
central ‘body’ and six sensors attached to it to form three symmetry axes. The
consideration behind the hexagonal design was to give agents sufficient liberty
of motion retaining the symmetry and thus leaving undefined the front and
the back. Sensors are combined into three identical axes which have a
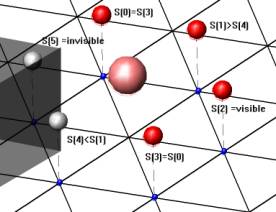
major influence over the activation function (see image no 2). Each sensor-axis
has four possible states: two polarized states (only one sensor active), both
sensors active, and both sensors passive. All three sensor-axes together yield
to a sensory space with 64 possible input combinations. Sensor morphology is
invariant, which means that the body plan of the agent is not capable of
evolving over time.