Fractal components in the Gothic and
in the Baroque Architecture
Professor Nicoletta Sala, Ph-D
Accademia di Architettura (Academy of Architecture) di Mendrisio.
Università della Svizzera Italiana (University of Lugano).
Largo Bernasconi, 6850 Mendrisio. Svizzera. E-mail: nsala@arch.unisi.ch.
Abstract
Fractal
geometry describes the irregular shapes and it can occur in many different
places, for example in Mathematics and in Nature. The aim of this paper is to
present an overview which involves the fractal geometry, the property of
self-similarity and the Iterated Function System (IFS) applied in two different
architectural styles: the Gothic and the Baroque.
1.
Introduction
In the different centuries the
architecture followed the Euclidean geometry and the Euclidean shapes (for
example, to realize the boards and the
bricks). Thus, it is not a surprise that the buildings had Euclidean
aspects. The geometric properties of the symmetry applied to the buildings and
to the temples helped to realize the engineering calculus, and to obtain the
structural stability. Some architectural styles, for example the Baroque, found
inspiration by the Nature, and the Nature is manifestly irregular and
fractal-like. So perhaps there is not difficult to find fractal components in
architecture [1, 2, 3, 4, 5]. As this paper will describe, fractals appear in
architecture to reproduce some shapes and some patterns present in the Nature.
This fractal analysis has been divided in two parts:
·
a small scale analysis, for example to determine the single building shape [4].
·
a large scale analysis, for example to study the urban growth and the
urban development using a fractal point of view [6, 7, 8].
The small scale analysis observed:
·
the
building's self-similarity, for example to find some self-similar components in the Baroque churches which repeat themselves in different scales,
·
the
Iterative Function System (IFS), for example to determine some iterative
fractal processes present in the Gothic style.
The paper is
organized as follow: section 2 presents a short description on fractal
geometry, in particular the self-similarity and the IFS. Section 3 and section
4 show the fractal components in the Gothic and in the Baroque architecture respectively.
Section 5 contains the conclusions, and the section 6 is dedicated to the
references.
2.
Fractal Geometry: the self-similarity and the IFS
A fractal object is self – similar
if it has undergone a transformation whereby the dimensions of the structure
were all modified by the same scaling factor. The new shape may be smaller,
larger, translated, and/or rotated, but its shape remains similar [9]. The
self-similarity is a property by which an object contains smaller copies of itself
at arbitrary
scales. “Similar” means that the relative proportions of the shapes’ sides and
internal angles remain the same. As described by Mandelbrot (1988), this
property is ubiquitous in the natural world [9]. Oppenheimer (1986) used the term “fractal” exchanging it with
self-similarity, and affirmed: “The geometric notion of self-similarity became
a paradigm for structure in the natural world. Nowhere is this principle more
evident than in the world of botany.” [10]
Self-similarity
appears in objects as diverse as leaves, mountain ranges, clouds, and galaxies.
Figure 1 shows a broccoli (Brassica oleracea) which is an example of
self-similar vegetable in the Nature. In figure 2 there is a Sierpinski
triangle that is a fractal object which presents the self-similarity. It has
been created using simple geometric rules.
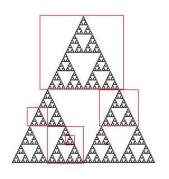

Figure 1. The broccoli is an example of Figure 2. The
Sierpinski triangle is an
self-similarity in the Nature
object derived by a simple iterative process
Iterated Function System (IFS) is
another fractal that can be applied in the architecture. Barnsley [11, p. 80]
defined the Iterated Function System as follow: “A (hyperbolic) iterated
function system consists of a complete metric space (X, d) together with a finite set of contraction mappings wn: X® X with respective
contractivity factor sn,
for n = 1, 2, …, N. The abbreviation
“IFS” is used for “iterated function system”. The notation for the IFS just
announced is { X, wn,
n = 1, 2, …, N} and its
contractivity factor is s = max {sn :
n = 1, 2, …, N}.”
Barnsley put the word “hyperbolic “
in parentheses because it is sometimes dropped in practice. He also defined the
following theorem [11, p. 81]: “Let {X, wn, n = 1, 2, …, N} be a hyperbolic iterated function
system with contractivity factor s.
Then the transformation W : H(X) ® H(X) defined by:
![]() (1)
(1)
For all BÎ H(X), is a contraction mapping on the complete metric space (H(X), h(d)) with contractivity factor s. That is:
H(W(B), W(C)) £ s×h(B,C)
(2)
for all B, C Î H(X). Its unique fixed point, A Î H(X), obeys
![]()
(3)
and is given by A = lim n®¥ Won
(B) for any B Î H(X).”
The fixed point A Î H(X), described in the
theorem by Barnsley is called the “attractor of the IFS” or “invariant set”.
Bogomolny (1998) affirms that two
problems arise [12]. One is to determine the fixed point of a given IFS, and it
is solved by what is known as the “deterministic
algorithm”.
The second problem is the inverse of
the first: for a given set AÎH(X), find an iterated
function system that has A as its fixed point [12]. This is solved
approximately by the Collage Theorem [11, p. 94].
The Collage Theorem states:
“Let (X, d), be a complete metric space. Let LÎH(X) be given, and let e ³ o be given. Choose an IFS (or IFS
with condensation) {X, (wn),
w1, w2,…, wn} with contractivity factor 0 £ s
£ 1, so that
![]()
![]()
(4)
Where h(d) is the Hausdorff metric.
Then
(5)
Where A is the attractor of the IFS.
Equivalently,
(6)
![]() for all LÎH(X).”
for all LÎH(X).”
The Collage Theorem describes
how to find an Iterated Function System
whose attractor is "close to" a given set, one must endeavour to find
a set of transformations such that the union, or collage, of the images of the
given set under transformations is near to the given set. Next figures 3 and 4
show respectively, the first two steps to create an image of a fern using the
IFS, and the Collage
Theorem applied to a region bounded by a polygonalized leaf boundary [11, p.
96].
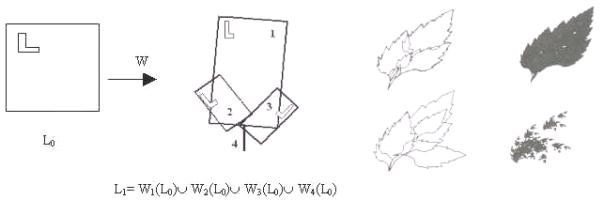
Figure 3. The first two steps to create an image of a
Figure 4. The Collage Theorem applied
fern [13, p. 116]
to a region bounded [11, p. 96]
The IFS are produced by polygons
that are put in one another and show a high degree of similarity to nature,
such as the fern presented in figure 5 [13, p.117]. The IFS form the connection
between the true mathematical fractals and the Nature.
The next sections describe some
applications of the self-similarity and of the IFS in the Gothic and in the
Baroque architecture.
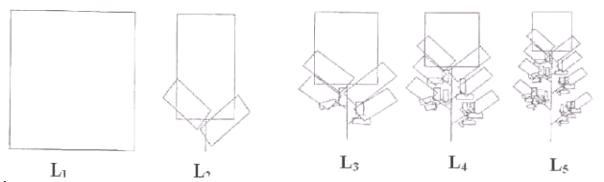
Figure
5. The first five steps to generate a fern using IFS [13, p. 117]
3.
Fractal components in the Gothic Architecture
The Gothic is a style developed in
northern France that spread throughout Europe between the 12th and
16th centuries. The term “Gothic” was first used during the later
Renaissance by the Italian artist Giorgio Vasari (1511-1574) as a term of
contempt. He wrote: "Then arose new architects who after the manner of
their barbarous nations erected buildings in that style which we call
Gothic".
Fulcanelli, the 20th century most enigmatic alchemist, gave
another explication of the term Gothic, which is connected to the language of
the alchemy[1].
Some fractal components are present
in the Gothic churches; an example is shown in figure 6 which reproduces the
facade of the Reims’ Cathedral
(1210-1241, Reims, France). The white arrows point out the fractal components
[13, p. 86]. The self-similarity is
also present inside the Gothic Cathedrals, as shown in figure 7.

Figure 6. Reims’
Cathedral (1210-1241)
Figure 7. Notre Dame (c.
1163-1250, Paris)
shows
fractal components shows a kind of the
self-similarity
Gothic architecture can be observed
using the iterative function system. The method is similar to the Wright’s
approach [15]. He dissected a fern in to similar part, and he marked some
triangles on these parts which are similar to the whole, as shown in
figure 8a). An affine maps was determined by how they map a single triangle to
another triangle. This allowed Wright
to convert out dissection of the fern into four affine maps. Figure 8b
shows the original four parts together with a triangle corresponding to the whole
fern, it is drawn in bold lines.
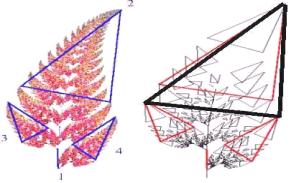
a) b)
Figure 8. Dissection of the fern into similar parts
a),
mapping
triangles for the fern b) [15]
Figure 9a illustrates an attempt to
find a IFS which could generate the ideal Gothic Church conceived by
Eugène-Emmanuel Viollet-le-Duc (1814-1879). The figure 9b is dedicated to
applied the same approach to a flower (Celosia plumosa) with is manifestly
fractal-like.

a) b)
Figure 9. An attempt to dissect a Gothic church in
self-similar parts a), the same approach applied to a flower (Celosia plumosa)
In the
Italian Gothic style there are many examples which show the presence of the
fractal components. In Venice there are many palaces (Ca' Foscari, shown in figure 10,
Ca' d'Oro, Duke Palace, and Giustinian Palace) that
have a rising fractal structure;
for this reason Fivaz (1988)
named this town: "fractal Venice" [16].
Santa Croce, the church of the Franciscans in Florence, is one of
the finest examples of Italian Gothic architecture. It was begun in 1294, in the period that served as the
transition from Medieval times to the Renaissance. It has been
designed by Arnolfo di Cambio (1240-1302), and it was finished in 1442, with
the exception of the 19th century Gothic Revival facade and
campanile. The church is simple basilica style with a nave and two isles.
Figure 11 illustrates the west facade of Santa
Croce, and an attempt to dissect it in triangles to find the IFS connected
to the church.

Figure
10. Ca' d'Oro (Venice, Italy)
(1421-1440) shows a fractal structure

Figure
11. Santa Croce (Florence, Italy ) an attempt to find the IFS
4. Fractal components in the Baroque architecture
The Baroque (1600-1750) was born in
Italy, and adopted in France, Netherlands, Germany, and Spain. The term
“Baroque” was probably derived from the Italian word “barocco”, which was a
word used by the philosophers during the Middle Ages to describe a hindrance in
a schematic logic. After, this have been used to describe any contorted process of thought or complex
idea. Another possible meaning derives by the Spanish “barrueco”, Portuguese
form “barroco”, used to describe an imperfect or irregular shaped pearl. This
word has survived in the jeweller’s term “Baroque pearl”.
This
style suggested movement in static works of art, and it influenced
important challenges in architecture
[17]. Baroque architecture was based on the mathematics [18]. The Baroque
architecture could be analysed using a fractal point of view [19].
Figure 12 shows a kind of
self-similar components present in the which illustrates the plan of church of Saint Karl (1715-1737, Vienna) where the
oval is repeated in three different scales.
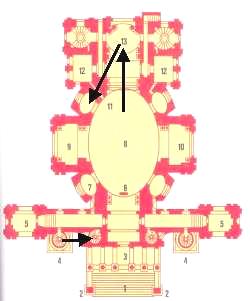
Figure 12. The
plan of the church of Saint Karl (Vienna)
shows some
self-similar shapes
Another example of self-similar
component is present in the church of San Carlo alle Quattro Fontane,
conceived by Francesco Borromini (1599-1667). The Swiss architect used the
octagons, the Greek crosses and other shapes for the coffering of the dome of San Carlo alle Quattro Fontane. The
figure 13a illustrates the valve lattice of the shell (Cakadia) which provided the brunched coordinates that map out the
Greek crosses and the octagons, shown in figure 13b, that Borromini used to
cover the dome of San
Carlo alle Fontane. The figure 14 illustrates the dome interior where the
ends of each lozenge and of each rhombus are unequal, the upper half of each
octagon is smaller than the lower half, and the top of the upright in each
Greek cross is shorter than the bottom of the lower part of the cross’ upright
[18]. Observing figure 14, it is possible to see the presence of two
directional compressions, horizontal and vertical at the same time, over a
(much shallower) dished plan. These compressions introduces a kind of
self-similarity in the dome [19].
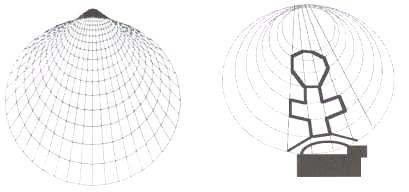
a) b)
Figure 13. The valve lattice of Cakadia a), the lattice used to map a detail in the
Borromini’s dome b) [20, p. 52]

Figure
14. Dome of San Carlo alle Quattro Fontane, Rome.
The arrows
connect the self-similar shapes
An other example of self-similarity
in the Baroque architecture is in the dome of Church of San Lorenzo (Turin, 1666-1680), designed by the Italian architect
Guarino Guarini (1624-1683). Norwich (1975) wrote: "The
Church of San Lorenzo, Turin, was begun by Guarino Guarini in 1668 for the
Theatine Order, of which he was a member. The plan is remarkable for its curved
bays pressing into the central domed space—an idea developed from Borromini—but
the dome is even more remarkable. It is a masterpiece of ingenious
construction—the ribs actually carry the lantern above them—which is also used
to produce dramatic contrasts of light and shade" [21, .p 176].
Guarini used the octagonal star to define the bearing structure of the dome.
The self-similar components are an octagon and an octagonal star which are
repeated in different scales, as shown in figure 15 [22, p. 85].
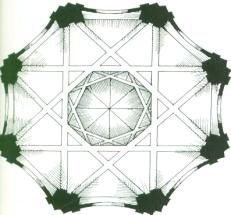
 Figure 15. The dome of San Lorenzo (Turin, Italy) shows some
self-similar components
Figure 15. The dome of San Lorenzo (Turin, Italy) shows some
self-similar components
5. Conclusions
Fractal
geometry and its connection between the complexity can help to introduce the
new paradigm in architecture [2, 5, 7, 8, 9, 10, 18]. This paper introduces
only an approach to observe the Gothic and the Baroque architecture using a
fractal point of view. The property of the self-similarity present in these two
different styles has been chosen for an aesthetic sense; in fact the Gothic and the Baroque architects did not
know the fractal geometry, because it is a recent discovery. Thus, it is possible to refer as an “unintentional” use of the fractal geometry.
The
modern architecture uses the self-similarity appears in intentional way [1, 2,
4, 13]. The iterated function system applied in the Gothic cathedrals could
help us to understand the generative processes of these complex buildings.
Recent
studies reveal that the IFS could help to create a new pseudo urban models based on fractal algorithms [23]. Thus, it could
be possible to encode simplified 2D½ city models using an IFS compression
technique.
6.
References
[1] Bovill,
C. Fractal Geometry in Architecture and Design, Birkhäuser, Boston, 1996.
[2] Salingaros,
N. I
frattali nella nuova architettura,
retrieved October 29, 2005, from:
http://www.archimagazine.com/afrattai.htm
[3] Sala, N.
The presence of the self-similarity in architecture : some examples, in M.M.Novak (ed), Emergent Nature, World Scientific, 2002, pp. 273-283.
[4] Eaton, L. K. Fractal Geometry in the Late Work of Frank
Llyod Wright: the Palmer House. Williams, K. (ed.), Nexus II: Architecture and Mathematics, Edizioni Dell’Erba,
Fucecchio, pp. 23 - 38, 1998.
[5] Sala, N., Cappellato, G. Viaggio
matematico nell’arte e nell’architettura, Franco Angeli, Milano, 2003.
[6] Frankhauser, P. La Fractalité des Structures Urbaines, Collection Villes, Anthropos, Paris,1994.
[7]
Frankhauser, P. L’approche fractale : un nouvel outil de réflexion dans
l’analyse spatiale des agglomérations urbaines, Université de Franche-Comté, Besançon, 1997.
[8] Batty, M.,
Longley, P.A. Fractal Cities: A Geometry
of Form and Function, Academic Press, London and San Diego, 1994.
[9] Mandelbrot,
B. The Fractal Geometry of Nature. W.H. Freeman and Company, 1988.
[10] Oppenheimer, P. Real time design
and animation of fractal plants and trees, Computer
Graphics, 20(4), pp. 55–64, 1986.
[11] Barnsley,
M.F. Fractals everywhere. Academic Press, Boston, 2nd
edition, 1993.
[12] Bogomolny,
A. The Collage Theorem. retrieved
September 15, 2005, from:
http://www.cut-the-knot.org/ctk/ifs.shtml
[13] Sala, N., Cappellato, G. Architetture della complessità. La geometria
frattale tra arte, architettura e
territorio, Franco Angeli, Milano, 2004.
[14] Fulcanelli, Il mistero delle cattedrali e l'interpretazione esoterica
dei simboli ermetici della Grande Opera,
Edizioni Mediterranee, Roma, 2000.
[15] Wright,
D.J. (1996). Designing IFS's: the Collage
Theorem, retrieved, September 30, 2005, from:
http://www.math.okstate.edu/mathdept/dynamics/lecnotes/node47.html
[16] Fivaz, R. L’ordre et la volupté, Press
Polytechniques Romandes, Lausanne,1988.
[17] Harbison, R., Reflections on
Baroque, Reaktion Book, London, 2000.
[18] Hersey, G., Architecture and
Geometry in the Age of the Baroque, University of Chicago Press, Chicago,
2000.
[19] Sala, N., Cappellato G.
The generative approach of Botta’s San Carlino. Proceedings 6th Generative Art Conference, Milano,
Italy, pp. 328-337, 2003.
[20] Hersey, G., The monumental
impulse, The Mit Press, London, 1999.
[21] Norwich,
J.J. (ed.) Great Architecture of the
World. Mitchell Beazley Publishers, London, 1975.
[22] Götze, H. Castel del Monte, Hoepli, Milano, 1988.
[23] Marsault, X. Generation of textures and geometric pseudo-urban
models with the aid of IFS, Chaos and
Complexity Letters, Sala N. (ed.), Special issue dedicated to the Chaos and
Complexity in Arts and Architecture, 2005 (in print).