Creating tiling by means of 2D graphics applications

MCs. N. Bogdanova

Department of Computer Science, Daugavpils University, Daugavpils, Latvia

e-mail: nelly@dau.lv, nellijabogdanova@inbox.lv

Abstract

Methods of creating patterns and ornament with the help of computer can be divided in to several groups. First way is programming or generating patterns and ornament. Other way is using of features and capacities of computer graphics software for the tiling. Such applications of 2D computer graphics as Corel Draw, Adobe Photoshop, and Corel Painter contain tools and mechanisms for crating tessellations, patterns, mosaics, and tiling. Tasks of paper are to classify methods of creating tiling in each application and discuss the problems and advantages of these methods. All methods we classify in to large group: filling methods and cutting methods. But each application has unique features for creating ornaments and tiling.

Introduction

Methods of creating patterns and ornament by computer can be divided into several groups. (A) Programming or generating patterns and ornaments and (B) constructing patterns and ornaments by graphics editors’ tools. Programming patterns and ornaments by means of simple geometric objects, such as a point, line, rectangle, oval is a simple and spectacular method for explaining the main constructions of programming languages. Tasks where graphic is used are very convenient for explaining assignment statement, conditional branch, cycles, recursion, users’ functions, and basic conceptions of object-oriented programming. Ornament and pattern programming tasks demand wide mathematical background and simultaneous using knowledge form different areas of mathematics. But ornament and pattern programming cannot be brought only to methodic aspect. Generating ornaments are a subject studied by computer graphics. The idea of constructing various ornaments and patterns lies at the basis of many developing computer games, where tessellations of different kinds are modeled. Such applications of 2D computer graphics as Corel Draw, Adobe Photoshop, and Corel Painter contain tools for creating tessellations and patterns.

We would like to examine methods of creating patterns in 2D graphics applications as well as problems, appearing in context with this process.

Let us determine some definitions. Such terms as tessellations, ornament, tiling, patterns are used synonymously. A fragment of a pattern is often called a motive, a tiling, a rapport. Further on we shall use such a term as ornament meaning a pattern, consisting of rhythmically regulated elements without visible connections, a recurrent element of an ornament will be called a pattern.

Let us consider some classes of mathematic tasks, which lead to ornament construction. In the process of choosing tasks we shall take into consideration the following thoughts: an ornament pattern can be constructed with the help of computer graphics applications, ornament construction mechanisms can be reproduced in the frame of the above listed applications. Studying mathematical tasks is aimed at:

1. To define what geometric figures can be used for constructing ornaments and how;
2. What are mechanisms of covering the surface with ornament patterns.

Periodic ornaments

Form of patterns

Let us confine ourselves to tasks of ornament and pattern construction, which totally cover the plane with non- intersecting fragments of an ornament or a pattern having a definite geometric form without visible lines of connection. Let us consider regular geometric figures as basic forms. This class of ornaments and patterns called regular tessellations.

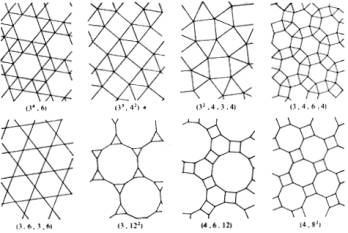
Regular, semi-regular and polymorph ornaments and tessellations. If regular polygons serve as patterns and two adjoining patterns have a common side, or only a vertex, then possible forms of patterns are equilateral triangles, squares, and regular hexagons. Ornaments, constructed having these rules are called regular (Figure 1).

Figure 1. Regular tessellations

If each vertex closes on the same number polygons of the same kind and in the same (or the reverse) cyclic order, there exit eight options of covering a plane (Figure 2), namely: 3·12²; 4·6·12; 4·8²; (3·6)²; 3·4·6·4; 3²·4²; 3²·4·3·4; 3⁴·6 (3⁴·6: each vertex of an ornament joins 4 triangles and a hexagon) [2, 3].

(3·6)^2 (3·12^2) (4·6·12) (4·8^2) (3^4·6) (3^2·4^2) (3^2·4·3·4) (3·4·6·4)
Figure 2. Semi regular tessellations	Figure 3. Demiregular tessellations

Tessellations of the plane by two or more convex regular polygons such that the same polygons in the same order surround each polygon vertex are called semi regular tessellations (Figure 2), or sometimes Archimedean tessellations. In the plane, there are eight such tessellations, illustrated above. There are 14 demiregular (or polymorph) tessellations (Figure 3) which are orderly compositions of the three regular and eight semiregular tessellations.

Transformation of pattern.. For two congruent tiles A and B in a tessellation, there will be some rigid motion of the plane that carries one onto the other. A somewhat special case occurs when the rigid motion is also a symmetry of the tiling. In this case, when A and B are brought into correspondence, the rest of the tiling will map onto itself as well. We then say that A and B are transitively equivalent.

Transitive equivalence is an equivalence relation that partitions the tiles into transitivity classes. When a tiling has only one transitivity class, we call the tiling isohedral. More generally, a k-isohedral tiling has k transitivity classes. An isohedral tiling is one in which a single prototile can cover the entire plane through repeated application of rigid motions from the tiling’s symmetry group. Note that an isohedral tiling must be monohedral, though the converse is not true [1].

By definition, an isohedral tiling is bound by a set of geometric constraints: congruences between tiles must be symmetries of the constraints can be equated with a set of combinatoric constraints expressing the adjacency relationship between edges of a tile. They proved that these constraints yield a division of the isohedral tilings into precisely 93 distinct types or families,1 referred to individually as IH1, . . . , IH93 and collectively as IH. Each family encodes information about how a tile’s shape is constrained by the adjacencies it is forced to maintain with its neighbours. A deformation in a tiling edge is counterbalanced by deformations in other edges; which edges respond and in what way is dependent on the tiling type, as shown in Figure 4.

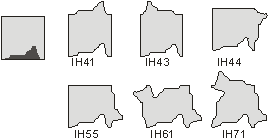
Figure 4. An isohedral tiling types

Isohedral tilings have the property that if you list the valence of each tiling vertex as you move around any given tile, the list will be consistent across all tiles in the tiling. This list is fundamental to the topological structure of the tiling and is called its topological type.

Methods of covering a plane with patterns

Symmetries. We know form mathematics, that there are three types of symmetries on plane: translation, rotation, glide-reflection. In reality meshes of regular ornaments, consisting of regular triangles and regular hexagons are identical. The it is enough to consider a square and hexagon, lying at the base of regular ornaments. Taking into consideration motion symmetries of plane in cells of regular meshes exist 17 types of regular ornaments (Table 1).

Table 1. 17 types of symmetries in regular tessellations [3]

Parallelogram (2x)	Rectangle(5x)	Rhombus(2x)	Square(3x)	Hexagon(5x)
P1-tessellations	PM-tessellations	CM-tessellations	P4-tessellations	P3-tessellations
P2-tessellations	PMM-tessellations	CMM-tessellations	P4M-tessellations	P3M1-tessellations
	PG-tessellations		P4G-tessellations	P31M-tessellations
	PGG-tessellations			P6-tessellations
	PMG-tessellations			P6M-tessellations

Ornament construction using tools of 2D applications

Let as analyze possibilities of computer graphics applications and problems arising in the process of periodic ornament construction on the basis of regular meshes by means of the isohedral tiling.

Ornament construction in Corel Draw

Basis objects. The vector graphics applications Corel Draw is a complete let of geometric figures for creating ornament patterns: a rectangle, convex polygons with a number of vertex exceeding 3. Lines, Bezier curves, oval can be used for creating patterns.

Creating patterns out of standard figures. Using auxiliary tools, such as Rules, Grid, Guidelines and snap to them and snap to objects considerably facilitates calculations and the process of construction. One should remember, that a grid can be uniform and non uniform and guidelines can be turned.

Alignment of objects. Possibilities of alignment operation were expanded in the twelfth versions of Corel Draw taking into consideration grid and specified points. Types of specified points and their options were also expanded and it helps to align to join figures flexibility. According to the author’s opinion alignment operation is more preferable in comparison with the usage, when logic functions or combine operation are expected to be used on aligned figures.

Constructing regular figures. Using CRTL key in the process of drawing a rectangle or polygon allows creating a regular figure. If there are some regular figures in pattern we recommend to create original figure out of equilateral triangles in order to construct a geometrically accurate ornament. There is no need in such case to create an equilateral triangle on the squire’s or hexagon’s side. The effect Blend can be used for creating regular figures.

Isohedral tiling in Corel Draw. A regular form of a pattern can be modified by mean of logical functions Trim, Weld, Intersection. Besides the direct effect Deformation can be used for pattern’s form transforming. The tool Envelope (e.g. Single Arc Mode and combinations of keys CTRL and ALT) can be used for patterns distortion taking into consideration the rules of isohedral tiling.

Figure 5. Examples of ornaments, created with the help of isohedral tiling

Methods of ornament construction out patterns in Corel Draw can be divided into the following groups: methods of cutting, methods of filling, methods of deformation.

Methods of cutting. Primitives, closed and non-closed curves, groups of the above mentioned objects can be used as original objects for cutting. In the order to construct ornaments, which cover the plane totally, it is necessary to have a closed curve as the result of cutting. Corel Draw tools for cutting - logical functions – Intersection, Weld, Trim – is directly meant for cutting, truncation and changing a pattern form. Trim method can be used for creating patterns by means of cutting a plane (squire, oval) with lines. The operation Break Apart is used for the next division of the sliced. The effect Power Clip can be used as an tool of cutting.

Problems arising in the process of figure cutting. A wrong object has been cut. Order of objects is of great importance for the logical operation Trim. The “main” object among the selected ones in the object, which lies either lower than all objects or it is than last selected for the Trim operation.

Break Apart operation is used for separating a complex figure into simpler ones. There are cases, when a slice figure, after this function having been used, splits apart into many non-closed curves, thought it seems that the figure consist of closed curves (especially it the figure has been cut by lines or non-closed curves). In such a case it is impossible to cut the figure gradually, in several steps. Another way of avoiding such a problem is not to use lines and non-closed curves, cut change them in to narrow rectangles or, for example, to transform a non-closed curve into a closed curve.

It should be noted that the analogous function Break… Group Apart must be used also for objects, which have been created with Corel Draw effects. As a rule these effects can be applied to a “simple” object or a group of objects.

Power Clip effect. This effect cannot be used. Possible reasons are either no object has been selected before using the effect, or the selected object is too complex, e.g. one of the effects has been applied to it.

The object being clip has disappeared after the effect applying. Such a situation can appear it the effect itself has been tuned default with automatic centering option of the object being clip and the circuit.

The object being clip has hit into a part of the circuit. Such a situation appears when the circuit has not been grouped beforehand. (A lot of problems are described in [5].)

Methods of covering. Any of the object copying or duplicating methods, as well as Blend effect can be attributed to methods of covering. It is convenient to use copying and, especially, duplicating, if ornament patterns are arranged regarding the translation. If patterns have been rotated it is preferable to use Blend effect.

Let us describe methods of creating ornaments with the help of Blend effect. Two objects participate in blending. Objects can be (1) simultaneously simple; (2) simultaneous groups of objects with the same number of objects, and a group created as a result of gliding and simplified into a group of simple object can be such a group; (3) simultaneously simple or a group, but the centre of rotation has been moving into the point, which is the centre of the rotation.

It is convenient to use Blend effect not only when a plane is covered with patterns, but both for creating patterns themselves and creating templates for cutting figures.

Problems arising in the process of using Blend effect. The most frequent reasons of problem arising are the following: (1) the number of objects, meant for Blend is not 2; (2) Blend effect is fulfilled between a simple object and a group of objects; (3) objects taking part in Blend effect has not been simplified [4].

Methods of deformation. Cloning. Before Corel Draw version 12 cloning operation can be used for creating patterns and ornaments. In principle the sequence of actions is the following. One of the regular figures of regular mesh must be the Master object. Then one of the regular meshes must be constructing with the help of any methods of covering, by means of Master object cloning. Transforming of the Master object with of transitive equivalence (isohedral tiling) synchronously reflect all transformations of clones.

Ornament construction in Adobe Photoshop and Corel Painter

The tricks of ornament creation in Adobe Photoshop, Corel Painter are as a whole identical.

The built-in tools of working with patterns allow creating ornaments on the basis of a rectangular regular grid. The mechanism of patterns filling is transition. A pattern, if it is not a rectangle and does not coincide ornament cell should beforehand be created so that it completely coincides with selected image part.

The greatest concern is represented by ways of ornament construction without visible lines of connection on the basis of photos and other images.

Usage transparency layer property in ornament construction. The part of the image, which must be as pattern should be located on a separate, transparent layer. As selection area it is possible to use only rectangular area and the selection area feather same as 0. As it is visible from a Figure 6B, C, patterns are beforehand constructed. The Figure 6D is obtained by multiple copying of a layer obtained by flood filling pattern from the Figure 6A. Pattern is in this case created with allowance for wide berths indispensable for creation of a lumen for underlying layers.

А	B	C	D

Figure 6. Ornaments constructed with regard of layer transparensy

The second method is more time consuming and it is based on image section cloning with the help of Clone Stamp tool (Adobe Photoshop) or Clone Brushes (Corel Painter) and multiple applying of filling procedure. This approach was described in [4]. Figure 7 demonstrates the sequence of actions with the help of which a pattern can be constructed. The first example of a pattern (Figure 7A) should be chosen taking into consideration the fact, that a pattern must contain, if possible, a section of image, which is notably less than an apparent pattern (compare Figure 10f and Figure 7B). After the first filling by the pattern (Figure 7B) junction lines can be seen on the ornament. So it is necessary to smooth out these junction lines, for example, around the central pattern (Figure 7C), and then add all the lacking details inside the pattern using cloning tool. If a pattern of the same side can be defines on the image once more (Figure 7C), than filling should be applied once more, than the resulting ornament (Figure 7D) will not contains visible junction lines between patterns.

A Define pattern	B Edit-Fill-Pattern	C Construction of pattern	D Ornament without visible junction lines

Figure 7. Creating ornaments using cloning tool

One more approach is described in [6], it is based on constructing a regular pattern out of fragments of various images taking into consideration the symmetric location of these fragments on a rectangular mesh (Figure 8).

Figure 8. Ornament construction with the help of pattern construction

Adobe Photoshop is filled with patterns only on a rectangular mesh. Where the sides of patterns accurately coincide. Additional possibilities of Corel Painter for ornament allow vertical or/and horizontal displacement with simultaneous scaling of patterns (Figure 9B, C).

A Dinamic layer Kaleidoscope	B	C

Figure 9. Using dynamic layer Kaleidoscope for pattern construction in Corel Painter

Corel Painter has a dynamic layer “Kaleidoscope”, which generates fractal patterns on the basis of image (Figure 9A). It should be noted, that in order to construct patterns transformation abilities of cloning brushes can be used in Corel Painter (xRotate 2P; xRotate, Mirror 2P).

A	B	C

Figure 2. Mosaic and Tessellations, created in Corel Painter

Besides tools for pattern construction Corel Painter has a tool for constructing tessellation. Mosaics can be created with the help of traditional technique, placing multicolored tilings of different forms on solid grout (Figure 10A), or o the basis of image (cloning technique) (Figure 10B). Tessellations are constructed by means of image automatic cutting into irregular tilings (Figure 10C).

Acknowledgments

Ornaments, patterns, tessellations are an independent kind of art, based on multiple repetition of an image fragment and image division. At the same time ornament construction is a vast group of mathematics tasks.

In 2D applications of computer graphics tessellations and ornaments with a periodical mesh and regular patterns can be constructed with the help different methods.

In vector application Corel Draw there exist wide choices of tools, effects that help to construct and transform patterns of regular tessellations in accordance with the rules of isohedral tiling. Ornaments construction can be done by means of figure division into parts, or filling the plane with constructed patterns.

Ornament construction in bitmap graphics applications Adobe Photoshop and fractal graphics Corel Painter largely coincides and it is optimal for ornament construction on the basis of images. But Corel Painter contains additional tools for patterns, mosaics and tessellations construction.

The topic of ornament construction has been included into academic courses of “Bitmap Graphics Applications” and “Vector Graphics Applications” of the professional study program “Computer Design” at Daugavpils University.

References

1. Kaplan, S.,C., Salesin, H.D. (2000). Escherization. Proceedings of SIGGRAPH 2000, in Computer Graphics.

2. Grunbaum B., G. C. Shephard. (1987). Tilings and Patterns. W. H. Freeman,.

3. Computer Art by Hans Kuiper. From http://web.inter.nl.net/hcc/Hans.Kuiper/index.html [11.11.2005]

4. McClelland, D. (1999) Photoshop 5. Bible. Hungry Minds.

5. Brain S., Scott Campbell, D. (1999). Special Edition Using CorelDRAW 9. Que.

6. Ilyin, M., Ilyina, M. (2002). Corel Painter 6. Snakt-PeterburgPublisher house "Piter". [In Russian]