Metaforms Methodology for specifying and growing Structures of Forms for Aesthetic and Programming Content

Dr Mark Rudolph PhD.

Institute for Innovation

Information Technology University Copenhagen

Rued Langgaards Vej 7

2300 Copenhagen

E-mail: mrudolph@yahoo.com

Abstract

Metaforms is a rule-based methodology for generating abstract and organic 3D forms (but capable of generating any forms expressible in symbol strings such as architecture music and text.) This paper introduces the conceptual basis of the methodology for 3D and describes its extensions to previous techniques for production systems. The generation of forms for a particular transformational syntax begins with a well-formed axiom of facts and a set of stylistic production rules which operate on the facts to produce a genotype. Facts correspond to transformations in 3D and particular locations for placeholder form components. Sets of rules fire by matching patterns on slots of facts which correspond to properties such as spatial orientation, position in the tree, and semantic description. There is an isomorphism maintained between the fact tree and a tree of Java transform objects which control appearance and behaviour in an interactive 3D (i3D) world. These Java objects are also used to calculate absolute 3D spatial state as the tree is traversed. This absolute state is then written into the slots of the transform corresponding to the component. Branches of the tree correspond to 3D transformations and leaves of the tree correspond to forms which are inserted in a later stage by population rules. The population rules map placeholder components to a phenotype of particular 3D forms expressed in syntax able to be rendered and programmatically controlled. The phenotype components consist of text or XML structures describing construction, property access and modification, method invocations and event bindings, and also include embedded annotations describing runtime semantics and operation. Phenotypes may be produced as static objects or made dynamic via a further stage of animation and variation using the programming interface to enable self-modification, movement and social behavioural interaction. The genotype syntax is intended to be an ontological universal for a particular domain such as 3D structures. In that case many individuals and groups could define domain specific genotype and phenotype structures and rules for behaviour so that same type structures may be capable not only of animation but also interactivity and breeding.

1. Introduction

The motivation for using generative systems for production of 3D objects is the difficulty and tediousness of modelling by use of tools and hand construction. The need for skilled labour on each individual piece using expensive tools drives up the cost of production and slows completion times. The situation resembles that of a Medieval guild in which expensive skilled artists labour extensively at one piece at a time. Biology inspired practices and rule-based programming offer a promising solution. A production methodology based on 'growing' instances instead of building them is efficient and automated, and the expression of stylistic preferences in rule sets permits decision making by an inference system instead of by human interactivity and tool use.

The basic terminology is borrowed from genetics and corresponds essentially to biological meaning. The fact tree consisting of hierarchical 3D transform information is referred to as the ‘genotype’ which in biology refers to the inheritable information carried by all living organisms [1.] In the specialized meaning used in metaforms the genotype is an abstract 3D structure with either no associated form or perhaps merely a simple bounding box at each leaf in the fact tree. The ‘populated genotype’ is a genotype in which all components contain a non-trivial String slot form in syntax which can be rendered and made visible in 3D space. Production rules act on an initial genotype ‘axiom’ and through iterative operation produce a more and more complex genotype. The real or potential form associated with each leaf is referred to as a ‘component.’ The closest biological analogy is to some fine grain element of the body such as cell or organ. In addition to the tree of facts, a parallel structure of Java objects is maintained and used when traversing the tree to calculate accumulating 3D transform information such as translation, rotation and scale, which are written into transform slots of the components contained at the leaves of the tree.

The ‘phenotype’ of an organism represents its actual physical properties, such as height, weight, color, shape and so on. In metaforms the phenotype is an isomorphic mapping of the genotype populated with a 3D form at each leaf expressed in a specialized syntax which can be both rendered visibly and programmed. Phenotypes are created by a different category of rules called population rules. A clear distinction between genotype and phenotype is that genotypes carry only structural information whereas phenotypes carry both structural information and phenomenal information about rendered forms. The structural element of the description might be thought of as the objectified process of moving a component in 3D by a sequence of hierarchical 3D operations. The form of a component refers to its shape, material, geometry, surface, and animation and behavioral properties.

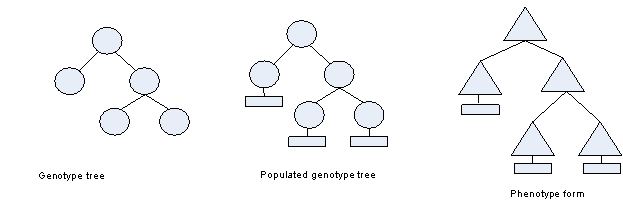
Figure 1

An organism's genotype is the largest influencing factor in the development of its phenotype, but it is not the only one. Even two organisms with identical genotypes normally differ in their phenotypes as can be seen in minor differences in identical twins. This divergence of appearance despite identical genotypes is emphasized in metaforms since arbitrary forms may be mapped by population rules to the leaf components of the genotype. In biological terms the phenotype in the proposed methodology has a very high degree of ‘plasticity’ because appearance is not strongly determined by genotype alone. On the other hand, a phenotype may be parsed in its specialized syntax and a genotype can be completely determined. This technique is used to synthesize very complex initial genotype axioms which determine much of the initial structure of the subsequent iterated genotypes and populated phenotypes.

It should be noted that genetic algorithms may be also be used as part of the metaforms system, but their actions are orthogonal to productions. The basic operations of crossover and mutation can easily be made part of the RHS of rules which select preferred tree nodes to perform crossover branch replacement or mutation modification of slot values. This paper will focus on rule-based development of single forms since genetic algorithms are extensively discussed elsewhere such as [7.]

2. Relations to previous work

There are two major streams of work which have advanced the subject of rule-based production systems. The strongest influence has been from Lindenmayer systems, or L-systems. A related stream of influence is the field of genetic algorithms and evolutionary artistic computation [2.]owever H This field is very important and interesting, but is orthogonal and not essential to the methodology of rule-based construction and population. There is a similarity in conceptual terms but production systems operate on a single genotype (or phenotype) and do not depend on the mixing of two or more individuals and the generation of populations. However genetic methods may advance the generation of content as an additional methodology applicable at any point in the production or population processes.

L-systems are based on rules for iteratively rewriting sequences of symbols for the purpose of describing the process of plant growth [3.] The key aspect of all generative systems is the encoding of rule-based processes in the development of forms. Predating L-systems is the mathematical constructions of von Koch [4,] and others including the great set theorist Sierpinski [5.] However, the early productions are abstract and fractal in nature whereas Lindenmayer began to propose rules for the organic productions of plant forms. A student of Lindenmayer,

Przemyslaw Prusinkiewicz, deeply advanced the scope and applicability of L-systems to computer graphics imagery [6.]

Traditional production systems use a tree traversal pattern match starting at the root and traversing the tree in pre-order fashion. These rewriting production systems share a parsing of a symbol string for rule matches and then substituting a matched substring by a new inserted string. Previous versions of metaforms also followed a similar technique. However the latest version uses a rule-based inference system which matches patterns on facts anywhere in the tree, and groups of rules can be applied as subsets in an orderly way triggered by previous rules. In addition, unlike production systems, metaforms transform facts contain a slot of ‘ontological adjectives’ which allow rules to match on semantic meanings in order to identify key structural locations or component qualities.

2. Rule-based systems

A rule-based system is a software system for reasoning about and transforming a dynamic fact base according to sets of rules. In the metaforms case rule sets capture stylistic preferences for iteratively defining and elaborating 3D objects as they develop in space. One possible view is that rules fire successively in time and the form developed is a sequence of time-based events each based on the context of the development to that instant. However, perhaps more accurate is to view the development of the 3D object as a collective set of internal transformations and variations from which a desired form emerges.

Rule-based inference is often used as the basis for ‘expert systems.’ In the case of metaforms the expertise captured in rule sets is a collective tendency to develop 3D form with certain stylistic preferences. Rule sets are then similar to swarms of tendencies operating on a potential form and in ways that social insects might construct a hive. There is no central control program but complex and intricate structures are produced by sequences of small transforms. Rules may act on any part of the structure in any iteration but the collective tendency is to produce a stylistic convergence influenced by the nature of the rules and the state of the developing form.

A rule-based inference system consists of a dynamic set of facts called ‘working memory,’ sets of rules called a ‘rule base.’ And an inference engine consisting of a pattern matcher, an agenda which holds the set of rules activated by matches on the present cycle, and an execution engine which fires one rule per cycle. A rule consists of a left hand side (LHS) ‘antecedent’ which is the specification of some state of fact(s), and a right hand side (RHS) ‘consequent’ which consists of actions such as method invocations, modifications assertions or retractions of facts, introductions of new rules, or modification of the set of rules able to fire in the next cycle.

Figure 2.

Before facts may be created they must first be defined in the same manner that a Class must be defined before object instances may be created. Facts may be simple lists or may consist of typed name-value pairs called ‘slots.’ Slots correspond to fields of a Class.

Rules are the key behavioural element in rule-based systems and the circumstances which activate a rule and the actions taken define the effect of the rule. Rules must be defined individually but the actions of subsets of rules must be anticipated to achieve directed stylistic effects. In addition priorities for rules may be defined, and strategies for ordering scheduled rule firings may be set and both varied during the running of the system.

The system runs in discrete cycles with at most one rule firing in each cycle. One cycle consists of the following steps:

(1) All rules able to fire in the present cycle are matched against the set of facts in working memory. Subsets of rules called ‘modules’ may be partitioned and only those rules in a particular module having ‘focus’ are examined for matches. The use of change of focus is very important for applying different subsets of stylistic and developmental rules at different phases of the structural development or at different locations in the structure.

(2) All rules with a LHS matching some fact are placed in a list in the agenda in the order of firing priority calculated according to a number of factors able to be specified and even modified at runtime.

(3) The first rule on the list (if it exists) then has its RHS executed which may modify working memory and take other actions such as adding to or modifying the structure or form. Thus at most one rule fires per cycle and that firing may invalidate other active rules. This completes one cycle of the process and the process repeats as often as desired.

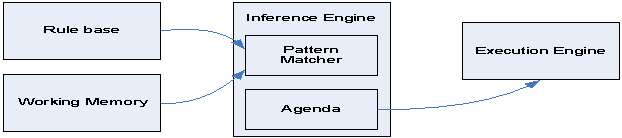
Figure 3.

Rule-based systems offer a new programming paradigm in which a large collection of tuned cooperating responses is able to guide a complex teleological purpose in effectively limitless circumstances and contexts, even some which the designer may not have imagined. Design expertise and stylistic preferences can be coded in the rules so that phenotypes produced by actions on genotype fact trees by rules from specialized stylistic modules produce similarly styled phenotypes but almost never are they identical.

The rule-based system used in the work described here is ‘Jess,’ written in Java and developed and maintained at Sandia National Laboratories by Ernest Friedman-Hill [7.] A key feature of Jess is its interactivity with general Java applications. In particular, rules may have RHS actions consisting of method invocation on Java objects, and general Java objects may interact in detailed ways with the embedded inference system. Other means of interaction are via prepared script files written in Jess syntax, and interactively by entering commands also in Jess syntax. There is one main class in Jess called ‘Rete’ which controls all activities of the inference engine.

It is also possible to save the state of working memory, or even the entire inference system to a file or a stream which permits persistence of metaforms sessions in time and migration of systems across space such as the Web. In addition, forms may maintain a reasoning system able to modify its own structure and behaviour or modify other forms and interact socially.

3. Realization and behavior in i3D

As mentioned previously, there is an isomorphism between the fact tree and a tree of Java objects which exactly represents the fact tree genotype and calculates accumulated transform values during tree traversal. Mirroring the fundamental Rete class in the Jess environment is a fundamental class ‘Tree’ in the Java framework. This class performs all operations on the Transform tree. Given an initial axiom fact tree, or a tree of facts persistently stored and then later reloaded, Jess can send the array of facts to Tree to create a mirroring Java Transform tree. If rules fire that make changes to the fact tree, additional RHS Tree method invocations synchronize the Transform tree with the fact tree and then recalculate the accumulated absolute Transforms below the point of modification and then writes the new absolute values into the Components at the leaves below the change. These updates are then sent back to the Rete object to update the slots of the Component facts. In this manner each domain specializes in what it is best at doing: Jess does pattern matching and rule firing whereas Java does matrix, vector and quaternion calculations.

There is, however, another reason for the isomorphic Java framework to the growing genotype.

At any point it is possible to request a phenotype to be written from any tree node. In the simplest case a special file is written to disk. The type of this file is VRML/X3D/MPEG4 which can be rendered and performed by specialized i3D players such as the Octaga player (www.octaga.com.)

In addition, the Java Transform objects contain native methods which can communicate with the i3D Octaga player. I designed a special JNI (Java Native Interface) link which I implemented jointly with designers at Octaga. By this means new nodes created by rule firings can also be created in the i3D phenotype and appear in the player. Similarly, modifications to existing facts of a populated genotype can be immediately seen as a transitory phenotype in the rendered i3D space. In particular, changes to the populated String form in facts are communicated to the i3D player and modify the appearance and structure of the phenotype.

It is the mirroring Java Transform tree which also has direct communication to the animation and behavioural capabilities in the i3D scenegraph. Because the RHS of rules may directly invoke Java Tree and Transform methods the inference system acts as the ‘idea’ for the phenotype ‘body.’ The full triad is a Jess ‘idea,’ a Java Transform controller ‘will,’ and an i3D ‘world.’

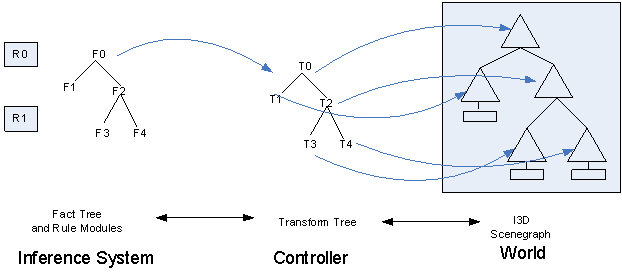
Figure 4

4. Operation of a Metaforms System

Metaforms is a process of creation and transformation so there is not one workflow path through its methodology. Also, since the process is cumulative and even sessional, it is better to think of the practice of form generation as an activity similar to the development and maintenance of software programs. In that respect the methodology resembles an integrated development environment with the possibility for extensions. Perhaps it is useful to recall the concept of action in the narrative theory of Aristotle. ‘Praxis’ contains not only the outward actions and events but also the inherent motivations which produce the outcomes. This motivational force in rule-based generative form creation is captured in two ways: the formulation timing of the use of the rule sets, and the formulation or choice of the axiom fact tree. Following Aristotle, the convergence of the metaforms methodology is a ‘poiesis,’ (roughly ‘making),’ and his Poetics itself is an analysis of the action of a poet in making a tragedy, and not simply an analysis of tragedy.

The fundamental interactivity of the process relies on the interactive interface offered by Jess, perhaps made simple and fast by a graphical user interface and search mechanisms for media assets including 3D components, image texture maps, and stored animation ‘gestures.’ Therefore the beginning of the session cannot be specified. It may be the importing of a previously stored session, or more simply, the importation of a fact tree which then serves as a de facto axiom. It may even be the simplest case of scripting the axiom directly and introducing that fact tree directly or by a script of that composition.

However it is presented to the inference system there are some specifications which must be made, similar to the need for ontological agreement before a communication based on symbols.

Specific to Jess, the ‘deftemplates’ must be registered in the system. These are the classes of facts able to be asserted. The structure of these facts corresponds isomorphically to the fields of Java classes, along with their accessors and mutators. Additionally it is necessary to define Jess functions to encapsulate actions common to many RHS of rules. These functions may contain direct calls to methods on Java objects such as Tree , the master static class controlling the maintenance and growth of the genotype tree.

Most critical is the definition of the modules of rules which are the actors of productions and populations. These are the specific subsets of styles and functions. They can be prepared and used or developed through experience, or developed genetically and valued by viewed analysis of effect.

Finally, after all the inference prerequisites, Jess can reflect its genotype fact base in Java by a static call to Tree ‘createTree‘ which mirrors the fact base by a tree of Transform objects able

to do calculations on the tree, modifications and recalculations, or insertions and retractions of fact Transforms and recalculations. A possible variation on this action is to view the default or populated forms of the genotype in an i3D viewer by sending down the phenotype syntax which can be rendered and viewed and programmatically altered.

A common procedure which may be illustrative is the following. Define or import an axiom of facts as an initial tree of facts which are then translated by Tree to a tree of Java Transforms. After that registration of facts and reflection to a Java framework rule sets modify and grow the genotype tree. In a further stage the default bounding box is populated by other rule modules by particular 3D forms. Finally, at any point in the genotype development a phenotype may be produced and viewed. Additional rule sets may be invoked which set animations and behaviours.

5. Conclusion

The metaforms methodology provides a powerful system for encoding stylistic tendency into rules operating on a tree of facts forming a genotype. The actions of these rules is analogous to the collective actions of a society of social insects, each never expressing a convergent goal, but together achieving a teleological purpose which is to produce variations of phenotype forms in a certain style. Rule sets can be grouped so that effects are specialized, and rules may also turn on and off modules to regulate the local influences according to conditions on the space or development of the genotype.

Furthermore, other cooperating rule sets may mark component placeholders by descriptive semantic adjectives expressing functionality or purpose, and further rule sets may then populate these component placeholders according to both absolute 3D spatial characteristics and semantic matches.

Next, behavioural rule sets may connect timers and interpolators and animation transforms for

movement and expression. Other rule sets may acquire output streams to destinations on the web and send their phenotypes and metaforms ‘minds’ to other hosts and environments able to reason in Jess syntax to appear and request to trade self-references with other entities of the same or similar types. Java reflection and annotation meta-information allow other rules to propose interaction or even breeding among any number of similar structures, and also cooperative or competitive social interactions. If all of these structures share the ontology of the encoded adjectives in the genotype nodes, then real communication and cooperation can occur and these migrating and fluent virtual entities may remake the virtual world.

6. References

[1] T. Bäck, 1996, Evolutionary Algorithms in Theory and Practice. Oxford University Press, New York.

[2] W Latham, S Todd, 1992, Evolutionary Art and Computers, Academic Press

[3] A. Lindenmayer, Mathematical models for cellular interaction in development, Parts I and II. Journal of Theoretical biology, 18:280-325, 1968.

[4] H. von Koch, Une methode geometrique elementaire pour l’etude de certaines questions de la theorie des courbes plane. Acta Mathematica, 30:145-174, 1905.

[5] W. Sierpinski, Sur une courbe dont tout point est un point de ramification. Comptes Rendus hebdomadaires des séances de l’Acadamie des Sciences, 160:302-305, 1915.

[6] P. Prusinkiewicz, Graphical applications of L-systems, in Proceedings of Graphics Interface ’86 – Vision interface ’86, pages 247-253, 1986.

[7] P. Bentley, D. Corne editors, 2002, Creative Evolutionary computing, Morgan Kaufmann, San Francisco

[8] E Friedman-Hill, 2003, Jess in Action, Manning Publications Greenwich Connecticut.