Generativity
and the Question of Space
Marie-Pascale Corcuff,
Architecte DPLG
DIPAU, Ecole d’Architecture de Bretagne, Rennes, France
COSTEL, UMR LETG 6554, Université Rennes 2,
Rennes, France
e-mail: m-p.c@wanadoo.fr
Abstract
First, space is
considered relatively to sensation, perception and representation. This leads
to defining notions like dimension, limit or cut, motion, ordering or arranging
of forms, and measure. Architectural space is examined through these notions,
and the issue of emptiness, or void, is emphasised. Then some experiments
(distance maps, and different growth processes) are presented in an attempt to
contribute to defining a generative space.
Space
What do we call “space”? And, first, what do we deal with when we think or speak of “space”?Let’s begin with very simple facts. In our human experience, we may distinguish at least four levels:
- first, there is the physical world around us (at least, we may suppose it exists);
- this physical world is known to us through our senses;
- the data coming through our senses leads to our perceptions;
- our perceptions lead to representations.
The way those levels have been ordered here is logical: if the physical world did not provide data to our senses, we would not be aware of anything. It is true that our senses are completed by all the devices we have invented to catch information about the physical world. Some of them are less acute than our senses (black and white photography, for instance), others go beyond (X rays radiography, infrared photography, etc.). But, most of the time, the results of these “sensing” instruments have to be “translated” in our human sensorial language to be understood (the result of a radiography is a translucent black and white film). So, as we cannot actually tell anything of the physical world without using our senses, we shall begin by (rapidly) studying our sensorial system.
Sensation
It is generally admitted that we have got five senses: the visual sense, the auditory sense, the tactile sense, the sense of smell, and the sense of taste; or, by way of the “actions” to which those sensations seem to refer (you may shut your eyes, or block your ears or your nose): seeing, hearing, touching, smelling, and tasting. This repartition seems natural, as each sense refers to a distinct organ: resp. the eyes, the ears, the skin, the nose and the palate. If our sensory organs were totally separated, the distinction would be unequivocal. But it is not really the case, and we know that our taste is affected when our nose is blocked. Disabled people, blind or deaf or affected by another sensorial deficiency, compensate their infirmity, partly, by relying on another of their senses: for “normally” seeing people, it seems really incredible to be able to “read” through the tips of one’s fingers, their sense of touching being too poor to allow such a skill.
Anyway, each sense can be distinguished (in any human language, this repartition is accepted), and each sense has its own specificity. For instance, the sense of view is a totally outer and even “at distance” sense, while touching implies. We can only see in a part of the universe delimited by the visual cone (roughly, in front of us) while we can hear in all the directions. Seeing is being affected by electromagnetic waves (light), while hearing is being affected by air vibrations (sound). This induces different kinds of sensations: low frequency sounds are felt, not only by our ears, but through our whole body, while light is not felt by anything else than our eyes (though infrared waves are felt as warmth by our skin).
Each sense is specific, but may refer to a multiplicity of phenomena: for example, our sense of touching allows us to know if a surface is smooth or rough, but also if it is cold or hot, though those two phenomena have little to do with each other when we refer to the physical world. For the visual sense, the primary data are colours, we must admit that colour as such is never separated from the characteristics of matter and is always perceived in space. Time-related events, like the frequency of sounds, or the wavelength of light, are not felt as such by us, but are translated in terms of, respectively, low or high sounds, and of colours.
However incomplete or lacking in some part our sensations are, they compulsorily give us a complete “space” (whatever this word refers to). That is not to say that becoming blind or deaf is not a handicap: that is obvious. But a daltonian, for example, does not feel a “hole”, a lack, in his own field or space of colours. We cannot imagine someone inventing or finding a “new” colour, different from the colours we already know. Such an idea is a “non-sense”, as Wittgenstein said [1]. Even if we know that a colour refers to a wavelength, and that there are wavelengths before and beyond those we can see, nothing on earth can make us “feel” those wavelengths as colours. Even if we have not actually seen all the colours at a certain stage of our life, new colours do not seem foreign to those we have already seen.
Moreover, the physical world, and particularly its spatial nature, is given as a whole. Sensorial data are not separately analysed by our brain, but contribute to a global perception.
Perception
In an article titled “Pourquoi l’espace a trois dimensions”[1] [2], Henri Poincaré defines what we have so far called a phenomenon (or even space) as a continuum: he takes the example of weight. This refers to our sense of touching (the idea here is not to use a balance, but to assess the weight of different objects by taking them in hand) and, moreover, to muscular sensation. We cannot distinguish between weights that are very slightly unequal: so we can make a “chain” of weights, each one slightly heavier than the precedent so that we cannot distinguish two successive “points” of the chain, though we clearly distinguish, for example, the first and the last. We can think of other continua such as the one of colour: with a computer you can easily find a chain of colours, indistinguishable one by one by the eye, and that goes, for example, from black to white, or that travels through red, blue, and green (fig. 1).
The most important characteristics of a continuum is that it has got a definite (integer) number of dimensions. The definition of dimension is topological and is made by recurrence, resting upon the notion of “cut”. The point is 0-dimensional; a line is 1-dimensional because a point makes a cut on a line: you cannot go beyond a point if you are on a line, a point cuts a line in two parts disconnected from each other; but a point, or any number of points, does not cut a surface: to cut a surface you need a line, so a surface is 2-dimensional; in the same way, neither points nor lines can cut a volume or space in separated parts, you can always find a roundabout way; only a surface or surfaces can cut a volume or space: so a volume, and space, is 3-dimensional. With this definition, you can prove that the continuum of weight is 1-dimensional, but that the continuum of colour is 3-dimensional: you can go continuously from black to white without passing by one particular colour, or even without trespassing any continuous line of colours, but a surface will block your way (fig. 1).
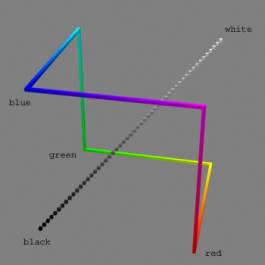
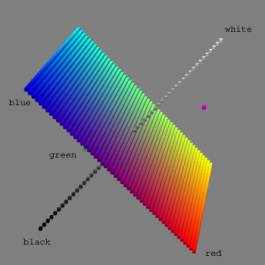
Fig. 1 The space of colours
Poincaré demonstrates that no one of our five usual senses, even if they are cooperating, is able to reveal to us the exact nature of common-sense “space”. The sense of view primarily furnishes our eye, and then our brain through the optical nerve, with rays of light, which attain the surface of the retina after having been focused by the crystalline lens: the visual sense is then bi-dimensional like the retina[2]; the “tactile” space, if we consider the whole of the skin, which is a surface, is also bi-dimensional at most, etc. To really be aware of the 3D nature of space, we must move, at least our eyes or our hand. To “read” the shape of an object with our fingers, we must move our fingers along its surfaces. To recognize our environment we must wander in it.
Human perception, through our senses, plus the kinaesthetic sense, reveals to us a 3-dimensional space, and not a more than 3 dimensions space. That is a fact, notwithstanding the “real” number of dimensions of the “real” space. For sure we can pursue the reasoning to, say, 4-dimensional forms or space, but to “see” what is a 4D object, we must project it in our 3D space (in the same way as 3D objects are projected in 2D by perspective). As displacements in 3D are translated by changes in the aspect of an object in a perspective (which is notably used in anamorphosis), displacements in 4D change the 3D object obtained by its projection from 4D to 3D. Poincaré suggested that if people in the future (his future, which is our present) learned to manipulate this projection in the same way as anyone does usual perspective, they would acquire an intuition about 4D space. That is actually possible nowadays with computers, and some people, in science or in art (Manfred Mohr [3]), have acquired such a skill.
Representation
We have encountered so far some notions that are inherent to the concept of space: dimension, cut, motion. The notion of form is implicit, because if there was nothing in any of the continua we have examined, at least points, these notions would be meaning less.
We have seen that the notion of dimension, inherent to that of space, is topological. That is to say that we need no Cartesian coordinates to deal with dimension. But, though we must not confuse dimension, in the mathematical meaning, and size, the continuum defined before leads to the notion of ordering, if it is 1-dimensional, or arranging, if it is 2 or 3-dimensional. Inside the continuum of weight, we may order weights (as points of this space) as lighter or heavier. We may even compare two weights and say that one is, for example, twice as heavy than the other. The weight space is 1-dimensional, and ordering it leads to a measure. The concept of colour (as others), generates its own “space” (independently from the physical space of figures and displacements), which we know is 3-dimensional, and that we can represent as well by a double cone with luminosity as middle axis, and saturation and hue as polar coordinates of the middle circle, as by a cubic portion of space with red, green and blue as basic vectors (fig. 1). We can say that this particular colour has more red in it than that other one, but we cannot totally order along a line all of the colours, or event arranging them on a plane, because this phenomenon is 3-dimensional.
Measure is applied to common-sense space, either 1-dimensionally (low/high, short/long, near/far, etc.), 2-dimensionnally or 3-dimensionally (big/little, large/small, etc.). We live on earth where there is gravity, and the configuration of our body leads us to favour a somewhat “natural” Cartesian representation suggested by words like left/right, in front/behind, below/above. But space is not only the structure of the world in which we live (as we perceive it), it is also for us a way of thinking. The characteristics of the space of figures and displacements are commonly applied to not-spatial fields (politics, feelings, etc.) as a lot of metaphorical expressions in any language show. It goes in both ways, and spatial words get affected by qualities (right is right, so left should be wrong…).
Representation implies thought and language. Phenomenology and cognitive sciences study these relations. Human beings do not only perceive, they think and they speak. But may we not add that they also draw, paint, build, etc? Concerning space, may we not suppose that concepts rely not only to language but also to these actions, this making of forms? In addition, the physical world in which we live is not only natural. It comprises also all the human-made artefacts, which, for the urban modern human being, are even most of what constitutes his daily physical world. May we not suppose that this environment has an impact on the personal and cultural perception and representation of space? Architecture has a central place in this issue.
Architectural space
Architecture may be called “art of space”, because it is an art that deals with all the characteristics of what we call “space”: with cuts (or limits), motion, measure; with dimension; and essentially architecture is a form game (by analogy with Wittgenstein’s language game), its essential preoccupation is the arrangement of forms (or voids, as we shall see).
Limits, motion, measure
Architecture deals with “limits”, a notion which is linked with that of “cut” as Poincaré defined it. Making architecture is, partly, playing with the arrangement of limits, which are not inevitably limits for all our senses. A (shut) window constitutes a limit for our displacements and for our tactile sense (wind blowing outside will not touch our skin), partly for our hearing (outside sounds will be muffled), but not for our visual sense. “Playing” (it is actually a very serious play) with the limits means, for example, concerning the envelope of a building, exploring intermediaries between opacity and transparency, as architects like Herzog and de Meuron, Soler, among others, do, with experiments with silkscreened glass or weaved metal, etc. Between no limit and strict limit, architecture plays with all the possibilities.
Architecture deals with motion. Architecture is not a strictly visual art (as painting and sculpture) because it needs being explored, wandered in, it is not given by a unique point of view (or “point” of another sense): it is what Le Corbusier called “promenade architecturale”. It may even be said that the labyrinth, or maze, is at the chore of architecture, and we must then remember that its drawing resumes the trace on the ground of the ritual dance that Dedalus made on the esplanade on which it was later built [4]. Between the straight line, as the shortest way between two points, and the maze, as the longest, architecture explores all the possibilities.
Architecture deals with measure. Some authors even consider architecture as essentially the art of giving measures to space. The notion of measure comes from the notion of scale, of proportion, and the issue of proportion is crucial for architects like Rudolf Schindler, Le Corbusier (Le Modulor), Dom van der Laan, etc. Establishing a system of proportion is indeed part of the art of space that is architecture.
Dimension
Architecture develops itself in 3-dimensional space, which means it deals with all that is possible, conceivable in that space, as we have just seen. But architecture does not deal only with the space of figures and displacements (the topological and geometrical space). Architecture, as all human artefacts, is part of the physical world, and as part of the physical world, is complicated. Forms are not only geometric, they are made with matter, they have got a colour, a texture, they are illuminated, etc. In an architectural space, you do not only confront with geometrical measures, but you are also cold, warm or hot, you may even feel sad or happy, etc. All those sensations are weaved inside us, and we tend to feel or sense the physical world as a whole, as we have seen in the first part of this paper. For the designer himself, geometrical and even topological issues are not the only ones he has to deal with, but a lot of other constraints: sociological, economical, etc.
Some authors have tried to translate all of these constraints or issues as “dimensions” of an hypothetical specific “architectural space” (or “architectonic space”), more complex than the topologico-geometrical one: Moore and Allen [5], or Philippe Boudon [6], to which we must be grateful for having tried to establish a rigorous architectural theory (which he calls “architecturologie”). Boudon draws a particularly long and disparate list of such “dimensions” or “scales” (expanding its meaning, from its usual homothetic field, to all of the constraints or qualifications that enter in an architectural design): the geometric scale, the cartographic scale, the functional scale, the human scale, the model scale, the optical scale, the parcel scale, the semantic scale, the neighbouring scale, etc…
We should be careful in interpreting such disparate parameters as dimensions, because in well defined spaces, basic vectors must actually be not-collinear, independent, but this independence must have a meaning: we can say that “blue” is not collinear with “red” and “green” (no amount of red and green will give blue), but we cannot say that “blue” and “hot”, or “blue” and “acute”, etc., are not collinear, because such a sentence is a non-sense.
Arrangement of forms
Since modernist architectural theory [7], “space” is a key-word for architecture. Not that there was no space in architecture before. But the word was not used, and the concept was not emphasized. Stressing on “space” means that what is important is not so much forms, but rather what is between forms, and the relation between forms. Void, or emptiness, is more important than matter, which relies to Taoist conceptions. Ching [8] quotes Lao-Tzu in the opening of his chapter “Form & Space”:
“We put thirty spokes together and call it a
wheel; but it is on the space where there is nothing that the utility of the
wheel depends. We turn clay to male a vessel; but it is on the space where
there is nothing that the utility of the vessel depends. We pierce doors and
windows to make a house; and it is on theses paces where there is nothing that
the utility of the house depends. Therefore, just as we take advantage of what
is, we should recognize the utility of what is not.” (Tao Te Ching 6th
century B. C.)
It is true that man does not live inside solid matter, but in the void (a not airless void, though) that lies inside, outside, or between solid forms.
Dealing with void, or emptiness, is not easy. Some have proposed to invert the representation codes, i. e. to fill in black (in plan) the empty, free, spaces versus the constructed ones [8, p. 95]. This makes us see an urban or architectural space in a different way. To qualify space, void space, more accurately, Ching introduces the notion of “spatial field” [8, p. 97.], or “field of influence” [8, p. 98.].
Pierre von Meiss [9], in a similar way, insists on the void, or the “hollow”:
“(…) pour l’architecte l’espace ou
l’intervalle entre sol, murs et plafonds n’est pas le néant, bien au contraire:
la raison même de son activité est de créer ce creux, pour contenir.”[3]
[von Meiss, p. 113.]
Meiss goes from Ching’s spatial fields to “lignes de force” or force fields to better characterize architectural space.
Generative Space
We have recognised four levels so far, even if some are overlapping: the physical world, and then sensation, perception and representation. The representation level may get its own autonomy, more yet since the use of computers. Generativity [10] has to do with the autonomy of the virtual world of computing. What can we do concerning space and forms? Or, rather, what can “it” do? What forms does a generative space “allow”. The virtual world of computer generativity lets us explore what happens when we imagine rules and let them develop by their own.
Distance maps
A first stage of exploration of space consists of trying to qualify the void, the emptiness, we have seen is at the chore of modernistic architectural space. The idea is to make sorts of maps of “emptiness” and to try to reveal the “forces” [9] underlying a given set of points.
In this first experiment we begin by establishing a set of “centres”. The algorithm used here is very simple (and, anyway, fast and efficient): it consists of calculating the Euclidian distance between each pixel of the map (the “space” here is bi-dimensional and treated as a picture: hence the appellation of “map”) and the nearest “centre” of the set, and of translating this distance in a grey level (fig. 2). This method has been inspired by the “medial axes” used by Gert van Tonder to explore the structure of Zen gardens [11]. If the set is a set of disconnected centres, the picture we obtain is a good approximation of a Voronoï diagram, the white lines emerging from the picture being possibly read as the lines of a Voronoï diagram.

Fig. 2: distance maps of a few distribution of centres
If the “centres” of the set are more connected, and are grouped in forms or shapes, the picture we obtain (fig. 3) emphasises and verifies the intuitive “spatial field” as sketched by Ching [8, p. 135, 158] or the force field defined by von Meiss [9, p. 125, 127, 129].

Fig. 3: distance maps of some configurations inspired by Ching [8, p. 135, 158]
The distance may be calculated in 3D-space. But then the issue of representing the results is more difficult. How to do a “map” in 3D? We meet here the limits of our perception: a map is a useful tool for us because it is 2D and that we are 3D, so we can see “inside” the map. But if there is information inside a real-life opaque 3D volume we are not able to see it (hence all the devices like radiography and scanners, etc.). We could imagine 3D space in a computer software that would apply, to each “pixel” in 3D, a given colour. But it is not what happens in most softwares[4], they rely rather on simplifications of 3D volumes constituted by faces inside which there is no “matter. After some not satisfying tries with levels of transparency, I packed a big cube with little cubes (15x15x15 of them), and decided on the presence of a little cube depending on the distance to the “centres” (fig. 4)


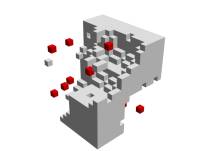
Fig. 4: 3D distance maps
After these experiments in 3D, I returned to 2D, and to randomness. The distance map algorithm was applied to a given random distribution of 20 centres in a square with a toric topology. A variant was obtained by translating the distance, or the level of grey, in the height of vertices of a mesh (fig. 5). The so-called centres are represented by spheres lying in the hollows of the “relief ” and the well marked creases of the mesh give a very good approximation of a Voronoï diagram.



Fig. 5: distance map of a given distribution of centres and the related mesh
Growth and struggle for space
The distance map is not very “generative”. It reveals the nature of a given space, but there is no process involved, while generativity has to do with processes. I went further by trying to exploit some systematic experiments I made for other issues on the notion of growth[5]. Growth is a fundamental mechanism of all natural forms, whether organic or not. We then can look at all the primary ways of growing that the rules of space allow. A first idea is to use the cellular automaton known as Conway’s game of life and to fix the rules to obtain a growth from a unique starting cell. A cell has got potentially 8 neighbours: we can vary the conditions for a cell to appear if it has m1, or m2, or … mn neighbours (m1, m2, … mn being comprised between 1 and 8). Figure 6 shows some of the results at t=20. There is a great variety of configurations, even if the rules are very simple.

Fig. 6: results of game of life at t=20 (“124” means that a cell appear if it has 1, 2 or 4 neighbours)
Even if it is not the most interesting one, we will retain the “123” growth which results in a square growing by adding a layer at its perimeter at each stage.
Rather than systematically explore the space of the CA at each stage, like in Conway’s game of life, we can also do a random exploration. This leads to a model we will call “propagation” (fig. 7). Those previous models are “static” CA, cells appear or disappear but they do not move. Other CA imply motion of cells, or “agents”. This motion is a random wandering, and the result is a growing cluster of cells. There are two ways of considering this growth: the cells may wander from outside towards the cluster, or they may wander inside the cluster towards the outside of the cluster. These two wanderings lead respectively to the well-known DLA model, and to a model we can call “proliferation” (fig. 7).



Fig. 7: “propagation”, DLA and “proliferation”
I got the idea of applying those growth processes to obtain Voronoï diagrams in Paul S. Coates’ paper for GA 2004 [13]. If we apply these models (the “DLA” model is slightly different because cells wander from random pixels without taking care of the distance to the clusters) to our previous distribution of centres, it looks as if each centre is at the chore of a “struggle for space” in different ways (fig. 8, 9, 10, 11).



Fig. 8: game of life



Fig. 9: “propagation”



Fig. 10: DLA



Fig. 11: “proliferation”
We can note that all these algorithms are a lot slower than the distance map one. They let cells or agents look for the nature of a space that is easily described through the distance map.
Optimisation vs sophistication
Though they may be slightly different, the results of all the previous models are about the same, and they are the same even if they imply some randomness.
We will now return to the so-called “proliferation” model. It was applied previously to the given distribution of centres by generating each cluster independently: the wandering started democratically from each centre, so each cluster had an equal luck in the struggle for space. We may also start the wandering with any one (randomly chosen) of the cells (proliferation variant #2): the result is that the clusters grow unevenly (fig. 12). The bigger they are the more they grow. Struggle for space is here more of a jungle law!



Fig. 12: “proliferation” variant #2
Now, each time we launch the process we shall obtain a very different result, though we start from the same set of centres (fig. 13).



Fig. 13: some results of “proliferation” variant #2
We may consider these two kinds of struggle for space as an example of the alternative between optimisation and sophistication. To stress this point, let’s compare the two models applied to a regular distribution of centres (fig. 14, 15).

Fig. 14: “proliferation” applied to a regular set of centres



Fig. 15: “proliferation” variant #2 applied to a regular set of centres
Without surprise, the patchwork obtained by the first model is more or less a multicoloured chessboard, while those obtained by the second one are more sophisticated patchworks. In the chessboard all the patches are (more or less) squares of the same size, they have got 4 neighbours, their borders join each others by 4. If your goal is to optimise the use of space, the chessboard is a good answer (it yields an regular tiling of space). In the variant #2 patchworks, even though the set of centres is the same orthogonal distribution, patches are of various forms, they have got a various number of neighbours (even 1, because some patches are enclosed in another one,), their borders join each others by, mostly, 3. If your goal is to obtain a more sophisticated use of space, where, for instance, patches need to have a various number of neighbours, and a more natural-like configuration, the variant #2 is a better answer.
In conclusion, we shall open the discussion with some remarks, that will not be further elaborated here. These experiments may seem very foreign to architecture[6]. Actually the issue is space by itself, notwithstanding all the other issues inherent to architectural space. The issue is space because those experiments deal with arrangement of forms or voids, with limits, with motion (motion of the cells), with measure and proportion (the sizes of the patches). The space in which these models develop themselves (which we call generative space) is a virtual, computed space. It is a particular sort of space, in that it is not, actually, a continuum (pixels are discrete points, numbers with which computers deal are not real numbers). Moreover, these experiments have been mostly developed in 2D, for obvious reasons of efficiency.
References
[1] Wittgenstein, Ludwig, Remarques philosophiques, Tel Gallimard, 1964 (1975 french translation)
[2] Poincaré, Henri, Dernières pensées, Flammarion, Paris, 1913
[3] http://www.emohr.com
[4] Le Dantec Jean-Pierre, Dédale le héros, Balland 1992
[5] Moore, Ch. & Allen, G., L’architecture sensible. Espace, échelle et forme, Bordas, Paris, 1981 (translation from: Dimensions. Space, shape and scale in architecture, Architectural Record, 1976)
[6] Boudon, Philippe, introduction à l’architecturologie, Dunod, Paris, 1992
[7] Giedion Siegfried, Espace, temps, architecture, Denoël (preface from Walter Gropius)
[8] Ching,
Francis D. K., Architecture: Form, Space & Order, 2nd
Ed., John Wiley & Sons, Inc., 1996
[9] von Meiss,
Pierre, De la forme au lieu: une introduction à l’étude de l’architecture, Presses polytechniques
romandes, Lausanne, Suisse, 1986
[10] Galanter, Philip, “What is generative art?”, Proceedings of 6th International Conference and Exhibition Generative Art 2003, available on http://www.generativeart.com/
[11] van Tonder, G.J., Lyons M.J. & Ejima, Y., “Visual Structure of a
Japanese Zen Garden”, Nature, 419:359-360. See http://www.ipc.kit.jp/~gert/publications/publications.html
for complete publications list
[12] Corcuff, M.-P. & Regnauld, H.,
“Automates cellulaires dynamiques et simulation de phénomènes directionnels;
croissance et dispersion”, Septièmes rencontres de Théoquant
“Nouvelles approches en Géographie Théorique et Quantitative”, 2005,
Besançon
[13] Coates, Paul S., “Review paper: some experiments using agent modeling at CECA”, Proceedings of 7th International Conference and Exhibition Generative Art 2004, Volume #1, p. 215-225; also available on http://www.generativeart.com/