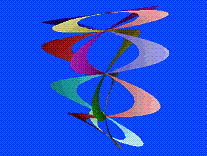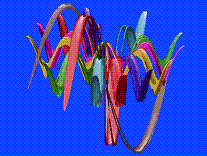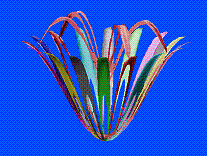Linear algebra and
creative process
F. Calio’, Professore di Calcolo Numerico
Dipartimento
di Matematica, Politecnico di Milano, Milano, Italy
e-mail : fracal@mate.polimi.it
E. Marchetti , Professore di Istituzioni di Matematiche
Dipartimento
di Matematica, Politecnico di Milano, Milano, Italy
e-mail : elemar@mate.polimi.it
Abstract
Mathematical methods
providing metamorphosis of
three-dimensional objects are considered.
Linear algebra is the basic tool : precisely linear transformations
depending on a parameter are the way to produce the basic surface,
moreover logic rules of manipulation of its parametric equations
allow the realization of the generative process.
We think that mathematical
methods introduced into a generative approach can increase the performances in
the designing evolution.
This paper illustrates an
example realized by modifying mathematically a three-dimensional form, whose
initial idea is recognisable at every step.
1. Introduction
When thinking of
mathematics, one can often think of an arid, however precise composition of
numbers, formulas, theorem proofs.
If one is more
open minded, one can also think of mathematics as of an indispensable support
to the applied sciences, such as physics, biology and chemistry for the
observed phenomena simulation.
One rarely
considers mathematics as a free expression of an idea allowing space for
imagination and the aesthetic sense. Yet mathematics means also this, and,
mainly this, for some mathematicians. Thus, a certain kind of mathematics -
inasmuch as it is free and abstract - is much closer to poetry and music than
to the exact and experimental sciences, to which it is commonly associated.
(Has anyone ever wondered why often those who are keen on music are also keen
on mathematics and vice versa ?)
The most
significant turning points concerning mathematical thought emerged out of
simple but deeply innovative ideas. One example of mathematical expression,
certainly originated by imagination more than by logic, is analytical geometry.
To imagine and to invent how curves, surfaces, classical forms and their
contraries could be represented not only with the help of drawing instruments
and the brush, but also through a few simple mathematical equations, demanded a
kind of sensitivity which neither the architect nor the poet possessed, yet
still one which, for its characteristics, we can name artistic.
One can naturally
make a different use of what has been imagined and then proposed to him/her.
(In poetry, for example, metrics can be considered both as a binding law that,
since it must be respected, can lead to correct, irreproachable, albeit sterile
results, and as starting point, a hint to create literary masterpieces :
it all depends on how somebody’s principles are interpreted and elaborated by
somebody else). Analytic geometry, just as metrics, can be used as a means to
classify and manipulate acknowledged shapes, but, above all, to elaborate new
ones, either already looked for or still unpredictable, thus opening the way to
new creative horizons.
Supported by the
idea that mathematics can be deemed intrinsically beautiful and creative and
that it can project its aesthetic and artistic taste on what it creates, we
would like to show, in this paper, how a few, simple, and accessible to
everybody mathematical proposals, offer pleasant and unpredictable graphic
results, which, according to us, can be included within a generative process.
These proposals both date back to the past centuries and are assisted by new
technologies.
More precisely we
will try and show how a plane figure, which may be generated and expressed
through formulas, can develop, either arbitrarily or according to a set aim,
into various three-dimensional shapes. A precise mathematical rule, one which
is apt to preserve through mutations those characteristics that can be defined,
even if not always appropriately, topological of the basic figure, will be
required here.
2. Use of the
mathematical instruments : a historical introductory description
Most surfaces and
curves in Greek geometry are defined through characteristic properties valid
only for them, which are generated, with the help of drawing instruments,
through ad hoc methods.
In order to
overcome this restricted method of operating, one needs a radically different
point of view, a method that can be applied to curves and surfaces, without
being distinctive of any of them, but rather more concerned with the main and
general features of the process than with its refinement and precision.
A decisive step
was made with the introduction of the Cartesian coordinates by the philosopher
and mathematician Descartes
(1596-1650). A point is characterised by its 
and 
coordinates : if
these vary without restrictions, the point describes the entire space, but if
instead the coordinates are bound by a mathematical law, the corresponding
point generally describes curves or surfaces. Complicated and intricate curves
have already been described since the end of the seventeenth century : among
them are the geometrical flowers by
the Italian mathematician Grandi
(1671,1742), a real virtuoso.
In analytical or
Cartesian geometry curves and surfaces are graphed by plotting points, being
thus totally independent from a curve or specific surface, which is defined
only by its equation. Cartesian formulation is therefore more powerful and
agile than that of classical geometry’s.
A further greater
flexibility is then obtained from the Cartesian coordinates system with the
introduction of parametric equations. The coordinates of the “moving” point are
described as a function of a variable
which changes linearly. These equations are more easily computable and
therefore lend themselves well to a graphic usage (particularly if
computerized). Moreover one can easily operate on them with matrix operators,
which in turn interpret geometric transformations algebraically.
The parametric
equations of geometrical shapes in addition to matrix operators are the only
instruments which we intend to use in order to realise the evolutionary process
of an object.
3.
Generative process
Let us take into
consideration a basic geometrical shape, namely a flower shape similar to a rodonea by Grandi.
The equation of
such a shape is determined according to the following algorithm :
· the parametric
equation of circumference belonging to the plane 
, with its centre
at the axes origin 
and of radius 
, is described as a set of vector points subjected to
infinite rotations, of angle changeable around the z-axis, and keeping the same distance 
from the rotation axis
;
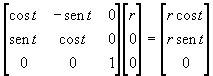
· the resulting
equation is modified, making the vector point regularly vary its distance from the rotation axis during the
rotation itself
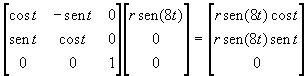
; (1)
· the following
parametric equations of the curve tracing the contour of the flower are obtained
.
|
|
Fig.1
Let us notice
from Fig.1 how the flower has 16 petals ; actually the distance of the
vector point from the rotation axis is zero for the angles 
(
).
· A flat surface
results from filling a proper area inside the contour of the flower ; we
obtain its equation by introducing a second parameter characterising, in a
variable way, the variability of the distance from the rotation axis
(mathematically, applying a scaling transformation with a variable scaling
coefficient to vectorial expression (1)).
, 
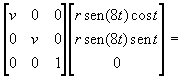
(2)
in Fig. 2 
.
|
Fig.2 |
The central idea
to the process consists now in developing this basic shape according to a fixed
mathematical law, although leaving the results a large margin of
unpredictability.
We have thought
of a metamorphosis law leading the flat-planed shape within the
three-dimensional space, through its projection upon different surfaces. From a
mathematical point of view this means that the third component of the vector,
describing the developing surface, must be properly subjected to variations.
More precisely, a
translation with translation vector parallel to 
-axis, whose length and direction follow the variations of
the 
-coordinates on the projection surface, is applied to
vectorial expression (2) of the basic
figure.
A first example
(Fig.3) shows the projection of the basic figure upon a surface of parametric
equations :
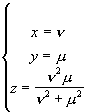
which, through
the following linear transformation,
=
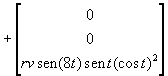leads to the
modification of the parametric equations of the basic shape :
|
Fig.3 |
Hence our
imagination was let loose ; the projection surfaces have been
progressively chosen for their greater geometric complexity and the figures we
obtained have taken unbelievable shapes, now light, subtle and elegant, now
strong and aggressive ; at times we can recognize them from their basic
shapes, at times we can’t, since they look absolutely different, but, full of
harmony or confused as they may turn out to be, they are nevertheless always in
tune with the geometry appearing on the chosen projection surface.
The colours
themselves, which have never been modified by graphic programmes, fade or
become more intense according to the shape alterations, spontaneously
contributing to the aesthetical research of the final shape.
One can remark
how the symmetry and the regularity of the projection surface are reflected on
the symmetry and regularity of the projected shape and how, on the contrary,
the discontinuities, the harshness and the asymmetries of the projection shape
can alter the original symmetry and regularity.
In the first
instance we obtain continuous and smooth shapes (Figs. 4-10), while folds or
edges become evident when irregularities arise in the derivatives of the
function used. Ultimately, discontinuities in the function and in its
derivatives can be limited to one point only (common to all petals) (Figs.
13-19), as along curves (Figs. 20-24).
|
Fig.4 |
Fig.5 |
Fig.6 |
|
|
|
|
|
Fig.7 |
Fig.8 |
Fig.9 |
|
Fig.10 |
Fig.11 |
Fig.12 |
|
Fig.13 |
Fig.14 |
Fig.15 |
|
Fig.16 |
Fig.17 |
Fig.18 |
|
Fig.19 |
Fig.20 |
Fig.21 |
|
Fig.22 |
Fig.23 |
Fig.24 |
Conclusions
All figures have
been produced with the help of a graphics animation programme, simple to use,
that is structured in such a way as to allow us to deal with the parametric
shapes and the algebraic expression of transformations in the best way. The
programme has been elaborated by our research group.
The results of
our work are to be seen in the images here reproduced, which at times have
pleasantly surprised even ourselves. Above all they have stimulated us and
suggested the way to single out further potentialities of the mathematical and
data processing instruments. Our aim then is to establish further processes for
the modification of a basic form and its arbitrary evolution.
Those, who may
like to use it, will decide how to deal with this typology of results. If a
mathematician, he/she could study geometry on a particular form ; if a
designer, he/she could devise an object to which the resulting shape may
function as a support, or more simply, if he/she feels like it, one could simply
enjoy its aesthetic quality.
References
[1] F. Calio’- E.
Marchetti - E. Scarazzini Operazioni e
trasformazioni su vettori Citta’StudiEdizioni, Milano (1996)
[2] F. Calio’- E.
Scarazzini Metodi matematici per la
generazioni di curve e superfici Citta’StudiEdizioni, Milano (1997)
[3] E. Marchetti Linee e superfici Citta’StudiEdizioni, Milano (1998)
[4] G. Grandi Flores Geometrici, ex Rhodonearum, et Cloeliarum Curvarum descriptione
resultantes (1728)
[5] J.N. Cederberg A course in modern geometry Springer Verlag, New York (1989)
[6] H.S.Macdonald Coxeter Introduction to geometry Wiley (1961)