Travels in Space and Time, Explorations of
Virtual SoundScapes, Multi-dimensionalism of Digital Music
Gabriel Maldonado
Fantalogica - Rome - Italy
http://web.tiscalinet.it/G-Maldonado
Abstract
Computer Music still keep some of the features
of traditional music, together with new ones. Rhythm, melody, harmony can still
be present in new musical paradigms, but new compositional parameters are
emerging, causing the old definition of the term "music" not always
to be appropriate to describe new phenomena of sonic art. This paper will show
some new paradigms of this kind of sonic art, as well as different view of old
ones.
I believe that any past dogma should be wiped
out when dealing with digital arts. The rebellion against tonality of the first
half of 20th century is surpassed now, and in my opinion, new music can use
harmonic intervals without generating the ideological problems which arose at
that time (even if there are still many people who don’t admit it). Actually,
digital domain opens a huge amount of unexplored worlds, making any past
ideological dogma a prison we should free ourselves from.
Nowadays, making music has many things in
common with visual arts and scientific research. Many musical parameters can be
applied to video arts, architecture, and vice-versa. Structure of sound has a
lot of similarities with many other physical phenomena such as inner atomic
structure, particle physics, astronomy, biology etc.
This paper will deal with new uses and
interpretations of old musical parameters (rhythm, harmony, melody)
together with a presentation of some of
the new ones. Debated topics are:
·
Harmonic/inharmonic
sounds, rhythm and melodies. Cycles, and the Deep Harmony.
·
The
inner structure and evolution of a single sound.
·
Generative
music: stochastic generation, algorithmic composition, levels of action.
·
Interpretative
music: Music generated by exploration of sonic architectures,
·
Musical
Travels in Space and Time: generative processes constrained by interpreter’s
gestures, state transitions between musical structural configurations.
1. Harmonics and Inharmonics
Scientific researches have shown that the inner
structure of a class of acoustic phenomena, called "pseudo-harmonic” sounds, presents many affinities with the vertical
structure of tonal music. It is almost sure that the evolution of western music
and most ethnic music has been influenced by this class of acoustic phenomena.
On the other hand, music evolution cannot ignore the importance of inharmonic acoustic phenomena and of the
sounds made of stocastic components
(i.e. that sounds normally called "noises"),
that actually are a superset of harmonic sounds. I’m convinced that dialectics
between Harmonics and Inharmonics, Determinism and Alea,
will drive us to the most interesting creative results.
1.1 Sound
Harmonic sounds
are those acoustic phenomena whose pitch
can be recognized by the listener. The most paradigmatic example of this class
of sounds is human voice, when singing vowels.
Also melodic and
polyphonic instruments (such as flutes, strings, pianos, organs, guitars,
vibraphones etc.) produce this class of sounds, in contrast with rhythmic
instruments (drums, cymbals etc.) that produce inharmonic sounds.
According to the
Fourier theorem, any sort of signal (audio or non-audio, however complex it may
be) can be considered as made up of a sum of elemental sinusoidal components.
What determines its peculiarities are amplitude, frequency and phase of each
sinusoid.
A harmonic tone
is made up of a set of sinusoidal components whose frequencies have harmonic
relation with each others. “Harmonic relation” means that each frequency is an
integer multiple of a fundamental frequency. So, for example, if the
fundamental has the frequency of 100 Hz (cycles per second) the other
frequencies will have 200, 300, 400, 500,.... Hz. So, apart phase and
amplitude, the peculiarity of harmonic signals is to have its partial
frequencies in harmonic relation. A consequence of this fact is that an
harmonic signal is periodic, i.e. it represents the same waveshape each lap of
time. What leads this class of sounds is the INTEGER LAW.
1.2 Noise
On the other
side harmonic signals are only a small subset of the total class of acoustic phenomena. Noise has a continuous
spectrum in contrast with the discrete spectrum of harmonic sounds (and with
some inharmonic sounds, such as for example those produced by bells, that have
a discrete specturm too, even if partials aren’t in harmonic relation with each
others; this can be considered a third class of sounds, placed between the
harmonic and inharmonic ones). Unlike harmonic signals, noise signals have no
repetitive pattern at all. Acoustic impression of a noise signal is quite
different from a periodic one. A noise signal can be considered as the sum of
all periodic signals of any frequency in the audible spectrum, having an
infinite number of sinusoidal partials. So, signals having a discrete specturm
are a particular subset of noise signals. Noise can be compared with Chaos (maximum entropy), whereas a
sinusoidal signal can be compared with Order
(minimum entropy). Perfectly periodic signals can be compared with Determinism, non-periodic signals with Alea. However, both worlds have been
useful in music, for timbrical reasons and for structural reasons as well.
It is almost
impossible to find a perfectly periodic sound signal in nature. All vocal and
instrumental sounds are quasi-periodic or pseudo-harmonic sounds. The most
simple reason is that a perfectly periodic signal must have a infinite length.
Any sound useable in music should have a finite duration instead, as well as an
amplitude envelope. Also, the partials of an acoustic sound follow integer law
only roughly, since normally, each partial has an independent pitch envelope,
and only the mean frequency value can be considered an integer multiple of the
fundamental. Maybe the only real harmonic signal is the whole universe itself
(the motion of atomic particles seems to have perfectly harmonic cycles, even
if this fact is still subjected to be investigated, I suppose). This opens an
intriguing philosophical debate, started since the ancient world, called the Deep Harmony, or the Harmony of Spheres.
1.3
Dialectics between Sound and Noise
Rhythm and
melody are the fundamental elements of almost all sorts of music, followed by
polyphony and harmony. All these kinds of features have strong relations with the
periodicity of cycles, i.e. with the
structure of harmonic signals. Maybe in history the inner structure of
harmonic sound signals influenced the emergence of the common structure of
music: it is demonstrated that the frequencial structure of most musical scales
has many things in common with the harmonic series.
Fifth and Octave
are intervals present in almost all cultures, and western diatonic scales have
a lot of dependencies from the integer law. I take it for granted that western
equally-tempered scale is an approximation of pure scales, that has be
introduced in order to simplify the
construction and the playing technique of chromatic instruments (organs,
cembalos, pianos and hard-positioned melodic instruments such as winds). I will
discuss in more detail this argument below.
Also, iterative
rhythms have many things in common with harmonic cycles, so they are directly
related with the structure of periodic signals. As K.Stockhausen has shown, a
periodic waveform can be perceived as a pitched sound or as a rhythm, depending
on the repetition frequency of its cycle. When its frequency is above the lower
threshold of human audibility range, we perceive a cyclic signal as a sound,
whereas, when the frequency is below such threshold, we perceive each cycle as
a rhythmic pulsation. On the other hand, rhythm is beaten and emphasized by
means of percussion instrument that have undetermined pitch, most of them
producing several classes of noise signals. Almost all percussion instrument,
both pitched and unpitched ones, have a strong noisiness located at the attack
section of its envelope, but most sounds produced by the other families of
pitched acoustic instruments present this peculiarity too, even if less
evidently. In particular, human voice is able to produce both periodic sounds
as well as noises: most phonemes are made of a consonant attack portion (noised
signal) followed by a vowel sound (harmonic signal).
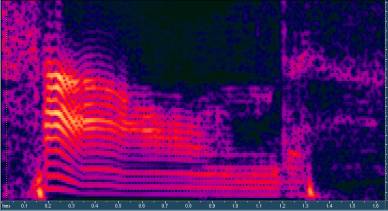
S
O U N D
Fig. 1 spectral sonogram of word “sound”.
Figure 1 shows
the sonogram of the word “sound”. We can clearly view the difference of
spectral structure between “noisy” letters (“s” and “d”) and “harmonic” letters
(“o”, “u” and “n”). Even if letter “n” is classified as a consonant by grammar,
actually its result is still an harmonic signal.
2. Using Structure of Sound to generate Musical
Structures.
In this section
some example of generation of musical structure (starting from the physical
nature of sound) will be presented. The structure of historical scales and the
basic elements of harmony and rhythm seem to be directly related to the nature
of the sound itself, showing a sort of auto-correlation between the inner
structure of sonic matter and its artistic elaboration. Even if I’m not
completely sure that in human taste, there is a native principle which induces
men to start from nature to put the basis of his artistic creations, I have
strong suspicions that this is the way things work.
2.1 Scales
Besides the
empirical and instinctive intuitions of ancient and ethnic musical practices,
which demonstrate that the inner structure of their musical scales has been
more or less influenced by physical structure of sounds, Grecian civilization
(mainly with Pythagoras) and modern age culture (Zarlino, Marsenne, Rameau and
others) have theorized the construction of scales based on relations between
integer numbers. Actually, both Pythagorean Scale and Pure
Scale (Just Intonation) are
based on harmonic structure. Scale configuration is the most basic element of
both melody and harmony (melody is the temporal succession of frequencies in a
single voice; harmony is the practice regarding the parallel configuration of
several contemporaneous frequencies, vertically layered). One can imagine a scale
as a “quantization” of the
frequencial continuum. Actually, this sort of quantization has almost always
been one of the most common forms of expression of singing voice. The same
thing is also valid for rhythm: iterative rhythmic patterns can be considered
as a “quantization” of a cyclical
sound wave.
Basic generative
intervals of most historical music scales have been Octave (factor 2 of the harmonic series) and Fifth (factor 3 of the harmonic
series), and, in some cases, Major Third (factor 5 of the harmonic
series). In Table 1 there is a
comparison of multiplier factors of Pythagorean,
Pure and Tempered musical scales. Such scales are generated by integer
ratios (that is, harmonic series), except the Equally Tempered Scale.
|
Frequencial ratios of sinusoidal partials of a generic harmonic signal |
||||||||||
|
Fund. |
2nd harm. |
3rd harm |
4th harm |
5th harm |
6th harm |
6th harm |
6th harm |
6th harm |
6th harm |
nth harm |
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
.....etc. |
|
Frequencial ratios of the Pythagorean Diatonic Scale |
||||||||
|
Grade |
Do |
Re |
Mi |
Fa |
Sol |
La |
Ti |
Do |
|
Ratio |
1 |
9/8 |
81/64 |
4/3 |
3/2 |
27/16 |
243/128 |
2 |
|
Frequencial ratios of the Pure Major Scale (Just Intonation) |
||||||||
|
Grade |
Do |
Re |
Mi |
Fa |
Sol |
La |
Ti |
Do |
|
Ratio |
1 |
9/8 |
5/4 |
4/3 |
3/2 |
5/3 |
15/8 |
2 |
|
Frequencial multiplier factors of the Equally Tempered Scale |
||||||||
|
Grade |
Do |
Re |
Mi |
Fa |
Sol |
La |
Ti |
Do |
|
Multiplier |
1 |
|
|
|
|
|
|
2 |
|
Multiplier factor comparison between the Pythagorean, Pure and Equally
Tempered Scales (converted to decimal notation). |
||||||||
|
Grade |
Do |
Re |
Mi |
Fa |
Sol |
La |
Ti |
Do |
|
Pythagorean |
1 |
1.125 |
1.265625 |
1.33333~ |
1.5 |
1.6875 |
1.8984375 |
2 |
|
Pure |
1 |
1.125 |
1.25 |
1.33333~ |
1.5 |
1.666666~ |
1.875 |
2 |
|
Eq. Tempered |
1 |
1.12246.. |
1.25992.. |
1.33483... |
1.49830... |
1.681792... |
1.887748... |
2 |
Table 1. Comparison between ratios of several scales.
N.B. Pythagorean and
Pure scales are directly related to the harmonic series, since they are derived
from integer ratios, whereas Equally Tempered scale has nothing in common with
the harmonic series (because its multipliers are generated from radicals and
are irrational numbers, with infinite digits after the decimal point), except
the fact that it approximates the values of previous scales.
Notice that the
degree of “consonance” of a pure interval (i.e. a frequencial interval
made up of an integer ratio), is determined by how much numbers of the ratio
are small. For example, the most consonant interval is the Octave (ratio 2/1), followed by the Fifth interval (3/2), the Fourth
interval (4/3), and so on. Comparing the previous tables we find that the most
“consonant” scale is the Pure Major Scale,
followed by the Pythagorean Scale.
The less “consonant” scale is the Equally
Tempered Scale, being made up of irrational numbers. Now, let’s go more in
depth, and let’s explain how Pythagorean,
Pure, and Equally Tempered scales are generated.
2.1.1 The
Pythagorean Diatonic Scale
Pythagorean
Diatonic scale is generated by means of a sum of Fifth intervals, and by wrapping around all the resultant values in
order to fit all them into the Octave
range. When speaking of frequencial ratios and using the term “sum”, we are actually referring to a
multiplication instead. For example, if we want to sum a Fifth interval to a Third
interval, we have to multiply their ratios (natural ratio of a Fifth is 3/2 and the one of a major Third is 5/4; to sum the two intervals
we have to multiply their ratios, i.e. [3/2] * [5/4] = 15/8). On the other
hand, when we want to subtract an interval from another, we have to divide
their ratios. In order to generate all ratios of the Pythagorean scale, we have
to start with the Fifth interval
below the Tonic. So we have to
subtract a Fifth interval (3/2) from
the Tonic (1/1) that is, to divide
the tonic ratio by the fifth ratio i.e. (1/1) / (3/2) = 2/3. In
order to generate all grades of the Pythagorean Sscale starting with this
interval, we have to add a Fifth
interval (multiplying each previous ratio by 3/2) for six times,. Then we have
to wrap around the results to fit them into the Octave range (Octave
ratio is 2/1 and, to add/subtract an Octave
to any interval, it is sufficient multiplying/dividing its ratio by 2), so:
|
Summing fifths to the intervals (i.e. multiplying ratios by 3/2) |
Grade of the scale |
Values wrapped around within the octave range |
|
2/3 |
Fa |
4/3 = 1.3333333.... = (2/3) * 2 |
|
(2/3) * (3/2) = 1/1 |
Do |
1/1 = 1 |
|
(1/1) * (3/2) = 3/2 |
Sol |
3/2 = 1.5 |
|
(3/2) * (3/2) = 9/4 |
Re |
9/8 = 1.125 = (9/4) / 2 |
|
(9/4) * (3/2) = 27/8 |
La |
27/16 = 1.6875 = (27/8) / 2 |
|
(27/8) * (3/2) = 81/16 |
Mi |
81/64 = 1.265625 = (81/16) * 2
* 2 |
|
(81/16) * (3/2) = 243/32 |
Ti |
243/128 = 1.8984375 = (243/32) * 2 *
2 |
So, by means of these simple operations, we have obtained all ratios of
the Pythagorean Diatonic Scale. The only subsequent pass which remains, is to
arrange the ratios in increasing order, that is:
|
Pythagorean Diatonic Scale (ratios) |
|
||||||||||||||
|
Grade |
Do |
Re |
Mi |
Fa |
Sol |
La |
Ti |
Do |
|||||||
|
absolute ratio |
1 |
9/8 |
81/64 |
4/3 |
3/2 |
27/16 |
243/128 |
2 |
|||||||
|
differential ratio |
9/8 |
9/8 |
256/243 |
9/8 |
9/8 |
9/8 |
256/243 |
|
|||||||
In this table differential ratio
between adjacent grade is also provided. Notice that, being Pythagorean
Diatonic Scale generated by ratios of integers, it can actually be considered as
a harmonic series (i.e. a series made up of integer numbers, even if the value
these number is quite high) if we eliminate the denominator of each ratio by
multiplying all ratios by 384:
|
Pythagorean Diatonic Scale (harmonic series) |
|
||||||||||||||
|
Grade |
Do |
Re |
Mi |
Fa |
Sol |
La |
Ti |
Do |
|||||||
|
Harmonic num. |
384 |
432 |
486 |
512 |
576 |
648 |
729 |
768 |
|||||||
|
differential ratio |
9/8 |
9/8 |
256/243 |
9/8 |
9/8 |
9/8 |
256/243 |
|
|||||||
Actually the full Grecian Scale system is more complex, having more
modes than the Diatonic, being based
on tetra-chords etcetera, but
entering in depth within this topic is beyond the purpose of this paper.
2.1.2 The
Pure Major Scale
Constructing
Pure Diatonic scale is a bit more complex and structured than Pythagorean
scale, but it is made up of more simple ratios than the Pythagorean one, so it
sounds more “consonant”. Its model can also be used to invent new classes of
scales, as I will show.
The basic
concept of the construction of Pure Major Scale is the Pure Major Triad. A Pure
Major Triad is a group of three frequencies proportional to the integer numbers
4, 5, 6. Actually numbers 4, 5 and 6 are the frequencial ratios of the fourth,
fifth, and sixth harmonic partial of a periodic signal. A brief parenthesis
about the relation between note names and harmonic number is needed now: for
example, when considering a periodic signal having a fundamental frequency of
100 Hz, the second harmonic will have 200 Hz, the third harmonic 300 Hz, the
fourth harmonic 400 Hz, the fifth harmonic 500 Hz, the sixth harmonic 600 Hz
and so on. So the relation between integer factors is validated. But the
frequencies of the first 10 harmonics can be also compared with the musical
notes. If the first harmonic (factor 1) is a C note, the second harmonic
(factor 2) will be a C placed an Octave
above. The third harmonic will be a G placed an octave plus a Fifth interval above the fundamental,
the fourth harmonic a C placed two Octaves
above the fundamental, the fifth harmonic an E placed two Octaves plus a major Third interval, and the sixth harmonic a G placed two Octaves plus a Fifth interval above the fundamental. So we obtain a major triad
C-E-G from the factors 4, 5, 6, considering the factor 4 as the triad
fundamental. The Pure Major Scale is simply made up of three Pure Major Triads: the Tonic
triad being the main triad, a Subdominant triad placed a Fifth interval below the Tonic (that can be obtained by dividing
all triad elements by 3, since 3 is the factor corresponding the first Fifth interval we encounter in the
harmonic series), and the Dominant triad placed a Fifth
interval above the Tonic fundamental
(that can be obtained by multiplying all triad elements by 3). So:
Tonic Pure Major Triad:
4, 5, 6 ![]() 1, 5/4, 3/2 (that are the same factors lowered by two Octaves in order to have number 1 as the
fundamental)
1, 5/4, 3/2 (that are the same factors lowered by two Octaves in order to have number 1 as the
fundamental)
Subdominant Triad (obtained by dividing the original triad by
3): 4/3, 5/3, 6/3 ![]() 4/3, 5/3, 2
4/3, 5/3, 2
Dominant Triad (obtained by multiplying the original triad by
3): 4*3, 5*3, 6*3 ![]() 12, 15, 18
12, 15, 18 ![]() 3/2, 15/8, 9/8 (the
same factors wrapped around inside our base Octave).
3/2, 15/8, 9/8 (the
same factors wrapped around inside our base Octave).
So, by arranging all obtained ratios in
increasing order, we obtain the Pure Major Scale again:
|
Pure Major Scale (ratios) |
||||||||||||||
|
Grade |
Do |
Re |
Mi |
Fa |
Sol |
La |
Ti |
Do |
||||||
|
absolute ratio |
1 |
9/8 |
5/4 |
4/3 |
3/2 |
5/3 |
15/8 |
2 |
||||||
|
differential ratio |
9/8 |
10/9 |
16/15 |
9/8 |
10/9 |
9/8 |
16/15 |
|||||||
If we eliminate the all the denominators by multiplying all ratios by
24, we obtain the following harmonic series:
|
Pure Major Scale (harmonic numbers) |
||||||||||||||
|
Grade |
Do |
Re |
Mi |
Fa |
Sol |
La |
Ti |
Do |
||||||
|
Harmonic num. |
24 |
27 |
30 |
32 |
36 |
40 |
45 |
48 |
||||||
|
differential ratio |
9/8 |
10/9 |
16/15 |
9/8 |
10/9 |
9/8 |
16/15 |
|||||||
Obviously differential ratios between grades remain unmodified. Notice
that the harmonic numbers of Pure Scale are much smaller than those ones of
Pythagorean Diatonic Scale, making it more “consonant”.
A picture showing the structure of the harmonic series so obtained
follows:
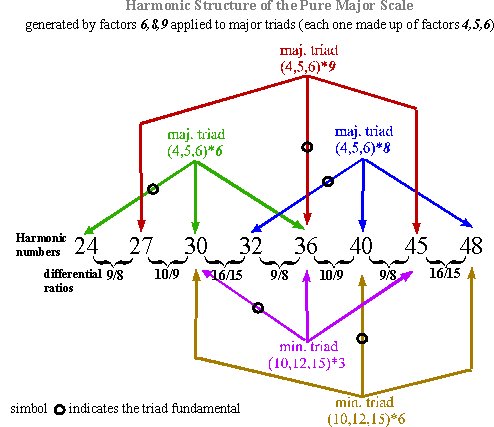
Fig. 2
The picture
shows that each Major Triad (made up of the factors 4, 5 and 6) is multiplied in turn by the factors
6, 8 and 9 that are
respectively: the Tonic itself
(factor 6), a Fourth interval above the Tonic
(factor 8, corresponding to the Subdominant, in fact, an ascending Fourth interval is a descending Fifth turned an Octave around) and a Fifth
interval above the Tonic (factor 9, corresponding to the Dominant).
Considering the
generative structure of the Pure Major Scale, we can use such method to
generate other scales. For example, the Pure Minor Natural Scale is made up
of three Minor Triads (each one of them being generated by the harmonic
factors 10, 12 and 15), the Tonic triad (factor 6, the same harmonic
factor of the tonic of Major Scale), the Subdominant
(factor 8) and the Dominant (factor
9). In this case the only difference with the Pure Major Scale is that, in this
scale, the three generative triads are Minor triads instead of Major triads,
but the tonic-subdominant-dominant multiplier factors are unchanged (6, 8 and
9) . These are the harmonic multipliers of Pure Minor Natural Scale and ratios
(all ratios have been wrapped in order to fit into the same octave).
|
Pure Minor Natural Scale |
||||||||||||||
|
Grade |
La |
Ti |
Do |
Re |
Mi |
Fa |
Sol |
La |
||||||
|
Harmonic Num. |
120 |
135 |
144 |
160 |
180 |
192 |
216 |
240 |
||||||
|
absolute ratio |
1 |
9/8 |
6/5 |
4/3 |
3/2 |
8/5 |
9/5 |
2 |
||||||
|
differential ratio |
9/8 |
16/15 |
10/9 |
9/8 |
16/15 |
9/8 |
10/9 |
|||||||
The Pure Minor Melodic Scale is made up of the
tonic-subdominant-dominant multiplier factors 6, 8 and 9, but in this case only
the Tonic triad is a Minor triad
(factors 10,12 and 15), whereas the Subdominant
and the Dominant are Major triads
(factors 4,5,6). All multipliers have been wrapped in order to fit into the
same octave.
|
Pure Minor Melodic Scale |
||||||||||||||
|
Grade |
La |
Ti |
Do |
Re |
Mi |
Fa# |
Sol# |
La |
||||||
|
Harmonic Num. |
120 |
135 |
144 |
160 |
180 |
200 |
225 |
240 |
||||||
|
absolute ratio |
1 |
9/8 |
6/5 |
4/3 |
3/2 |
5/3 |
15/8 |
2 |
||||||
|
differential ratio |
9/8 |
16/15 |
10/9 |
9/8 |
10/9 |
9/8 |
16/15 |
|||||||
We can also invent completely new kinds of scales by starting from
groups of harmonic multipliers chosen arbitrarily. For example, we can choose a
trichord different from a triad as the base element of a scale, as well as a
chord made up of more than 3 notes. In all above examples, we used the factors
6, 8 and 9 as multipliers (Tonic, Subdominant
and Dominant), but in scales of our creation, we can choose any other integer
number corresponding to other musical harmonies, different from the canonical
Tonic/Subdominant/Dominant structure. Actually, the number of ways we can
create new scale systems using the harmonic series is practically infinite.
2.1.3 Scales
generated by radicals: the Equal Temperament
The most common
used scale of the age we live, i.e. 12-stepped Equal Temperament, is a
very strange an curious case. In fact, the mathematical method to generate the
12 semitones of the equally tempered chromatic scale is totally different from
the ones of Pythagorean and Pure scales. But, for an incredible coincidence of
nature, we can choose some of the 12 semitones to arrange scales whose ratios
values are very near the values of Pythagorean and Pure Scales. For this
reason, and because of the spreading and intensive use of modulation as
compositional method in tonal music of the modern age, the Equally Tempered Scale made other kinds of scales to sink into
oblivion, at least until the computer age of nowadays. Actually Equally
Tempered Scale has made it easier the manufacture of some classes of acoustic
instruments, such as the keyboards (organs, cembalos, pianos), and any kind of
hard-pitched instruments (most wind instruments, vibes, xylophones etc.). In
order to celebrate the introduction of the tempered scale, J.S.Bach wrote the
two books of the “Well Tempered Clavier”, even if it is almost sure that Bach’s
temperament was not equal, since, at his time, several kinds of unequal temperaments were commonly in
use. The reason was that the ears of musician of Bachian age, still noticed the
harsh roughness of temperaments, and tried to mitigate their inaccuracy, by
introducing several kinds of temperaments, to be used in different situations,
according to the tonalities and modulations of pieces. Nowadays, people are so
much accustomed to Equal Temperament, to consider Just Intonation strange and
odd. In fact, even if very near, the ratios of Equal Temperament are not
exactly the same of the scales generated by the harmonic series. These
differences are noticeable especially in chords. Also, some particular
instrumental timbres make it more noticeable the difference (for example the
timbres with high harmonic content such as the cembalo). Actually, when hearing
a tempered scale, human brain makes some unconscious adjustments to interpret
his perception of tempered intervals according to the corresponding natural
intervals. These adjustments strain the hear, when listening music for a long
time. Furthermore, Equal Temperament provides a unnatural harmonic and melodic
hearing, and its structure of equally dividing the octave, makes music
production easier, but musical results sound standardized and monotonous. So,
together with the advantages, there are several disadvantages one should
consider when using Equally Tempered scales. Today, with the computer, it is
possible to choose what intonation system a composer intend to use, without
having to support the weight of the practical restrictions imposed by acoustic
instruments.
However,
temperament is an easy way to create new scales. Let’s see how much easy it is,
by generating a chromatic scale.
First, choose
the
main interval we intend to equally subdivide. This interval is normally
the Octave (ratio 2/1), but the
contemporary composer is not forced to use it. For example, we can use a Fifth (ratio 3/2), an Octave plus a Fifth (ratio 3/1), or
any other interval.
Second, choose
the number
of steps the main interval has to be subdivided. In the case of
standard semitone chromatic scale, the number of steps is 12. But if, for
example, we want to subdivide the Octave into 24 steps (quarters of tone), it
is only an arbitrary choice.
Third, generate the interval
multipliers by means of radicals. The general formula to
obtain a single step multiplier is:
step_multiplier = ![]()
that is: step_multiplier = ![]()
For example, to generate the step multiplier of
a quarter of tone, (that is, a single step of the scale obtained by dividing
the Octave by 24 parts) you need to apply the following operations:
quarter_of_tone =![]()
This operation generates a single step
multiplier. The general formula to create the multipliers for all steps, you
can apply the following:
![]()
being ![]() the quarter of tone multiplier in this case.
the quarter of tone multiplier in this case.
Any chord based
on intervals of a tempered scale, actually generates non-periodic signals, and,
consequently, inharmonic signals (even if they can roughly approximates
harmonic signals), whereas all chords based on intervals belonging to the Pure
or Pythagorean scales, as well as any scale based on harmonic series, generate
harmonic signals. So, only dissonant intervals are
theoretically possible when using an equally tempered scale, except the Main Interval (i.e. the Octave, in the case of both canonical
scale of 12 step, and the quarter of tone scale of 24 step), even if these
dissonant intervals could approximate a consonant one.
2.2 Creating
new scales, considerations
Being a scale
one of the first choice of the act of composing, I consider the choice of a
preexistent scale, or the creation of a new one, a real compositional act. This act is very similar to parameter mapping, a fundamental compositional act of Generative
Music (in some case parameter mapping is the only compositional act of a
generative work). I will treat of this in next sections.
By the practical
point of view, any kind of new scale can be easily managed with computer
synthesis and compositional programs such as Csound. MIDI protocol, if
considered alone, is not smart enough to manage micro-tuning, and commercial
electronic musical instrument companies are not seriously interested in providing
the user with a flexible tool for non-conventional music making (even if some
partial and unflexible attempts in this have been done by few electronic
keyboard manufacturer), but prefer to influence customers to permanently stay
in a trivial and standardized, but commercially secure and profitable
status-quo.
3. Interpretative and
Generative Sonic Arts
As we saw in
previous sections, pitched sounds themselves have an inner frequencial
structure. Even if this structure is approximated in most sounds (only sounds
generated by the computer with mathematical formulas could have an exact
harmonic structure, all acoustic sounds follow harmonic model more or less
roughly), the model based on harmonic series has been almost always followed in
the history of music, except for rhythmic instruments. Notice that harmonic
structure of sound was perceived only empirically by musicians, until the time
of Jean Baptiste Fourier (18th
century) who proposed a mathematical theory about harmonic series (according to
this theory, any kind of signal can be represented as a sum of sinusoids, each
sinusoid having its independent amplitude, frequency and phase), and until the
experiments of Hermann Ludwig Ferdinand
von Helmholtz (19th century), who experimentally validated the
theory that partials of pitched sounds follow the harmonic series structure.
3.1 Structure
of Music in Western Tradition
Using the
structure of sound to construct scales, is the first step to organize a musical
structure. The second step is arranging the elements of the previously chosen
scale horizontally (i.e. melodically) and/or vertically (i.e. harmonically).
Usually, a hierarchical structure is followed in these steps, at least for
classical music ( the “classical” term being to indicate all kind of western
cultured music, except contemporary music, in this case). In western tradition,
the first elements of this structure are the concepts of voice and chord.
If we consider the musical notation commonly used in western music (for example
the pentagram, or the graphic scores of contemporary composers) we can notice
that it resembles a Cartesian graph,
in which time is represented horizontally, passing from left side to right
side, and pitch (frequency) is represented vertically (frequency increasing
direction being down to up). Notice that a two-dimensional sheet of music is
able to graphically represent only two parameters: time and frequency. In
traditional music notation, amplitude is represented with some text or captions
(such as ff, mp, pp etc.) or some graphic signs ( for example ![]() ), that, anyway, give the interpreter only some approximate
information about the real value of amplitude.
), that, anyway, give the interpreter only some approximate
information about the real value of amplitude.
3.1.1 Voice
and Melody: the Horizontal Element of Music
Voices are the
main horizontal elements: they are made up of different frequency slices (notes), that are displaced serially, in succession.
The structure of a voice is the displacement of several frequencies in the time domain. A note succession is called
melody,
but this is a generic term. Actually, a
melody is structured into lower-level elements, made up of groups of notes.
Also these note groups can be hierarchically and recursively divided into
sub-groups. The interrelation of both note durations and their time displacement, is the rhythm
of the melody. Frequently, different note groups (belonging to the same melody)
can present some similarities both in rhythm and in frequency intervals. This
artifice provides unity, coherence and consequentiality both to the melody
structure and to listener hearing. A melody is often compared to a speech, it
has (at least inside the strong classical style) periods, sentences, phrases,
clauses, and words. For this reason music is often compared to a language,
having its grammar. But I believe that in music, differently from spoken
languages, there is no difference
between the meaning and the medium, i.e. the physicity of the medium, the
perception of the sounds themselves contains the meaning of music. Music significance
is its perception itself.
3.1.2 Harmony
and Chords: the Vertical Element
While it is
impossible to think to melody structure without the time displacement of the
notes, a single chord already contains a structure without considering time domain, being chords made up of a
group of notes displaced vertically, in our Cartesian graph comparison.
Actually, a single chord structure is a group of notes displaced in the frequency
domain. Harmony is the topic concerning both the structure of a single chord,
and the displacement of several chords in time domain. Harmony rules also
control the interrelations of several melodies flowing in parallel.
Many harmony
rules have been extrapolated by the theorist of classical music. Such rules are
simply a compendium of the usual procedures followed from the community of
composers belonging to a determinate age and current. Actually, composers
themselves govern the evolution of these rules. For example, one of the most
famous harmony rules is the prohibition to do parallel Octaves or Fifths between
two different voices. But, curiously, the first expression of harmony and
polyphony of western music was the so called “Organum” a musical form made up of a Gregorian melody together with
its parallel transposition a Fifth up
or down. Musical rules are subject to change in different ages, and can always
be broken by composers. An important thing composers should take into account,
is the good audibility of their
music. Unfortunately, in some historical periods (such as the second half of
the 20th century) composers have been more interested in theoretical
and formal structure problems, than in the audibility of their music,
forgetting listener hearing. Even if this approach could be useful under
certain aspects, and surely presents some intellectual interest, it has lead
music more and more distant from public.
A chord,
according to classical tradition, is generated by superimposing Third intervals once a time. So, a chord
of three notes is made up of a fundamental, a note placed a Third above the fundamental, and a note
placed a Third above the second one
(last note is actually placed a Fifth
above the fundamental). This kind of chord is called Triad. There are several
classes of triads (for example, minor
triads, major triads etc.). A chord made up of four notes is called also
a 7th chord, because last note is far a Seventh from the fundamental. Going ahead, there are chords of 9th,
11th and 13th, all generated by superimposing Thirds. All these chords are often
generated by using a diatonic scale derived from the Equally Tempered scale.
Obviously, chords generated by superimposing thirds are only a small subset of
all possible chords, but they have been almost the only kind of chords used
until 20th century. In 20th century some new kinds of
harmonies have been introduced (for example, Hindemith proposed a method of
generating chords by superimposing Fourths,
instead of Thirds and Jazz harmony
introduced some dissonant chords that would never been admitted by the classical
school).
A chord can also be used to generate a scale,
as we saw in previous section regarding the Pure Major Scale. For example, I
theorized a new kind of triad, made up of fundamental, and of superimposing two
Major Second intervals. In this case
all intervals are Pure intervals with the following ratios:
|
Triad of Second Intervals (ratios) |
||||
|
Grade |
Do |
Re |
Mi |
|
|
Harmonic num. |
8 |
9 |
10 |
|
|
absolute ratio |
1 |
9/8 |
5/4 |
|
|
differential ratio |
9/8 |
10/9 |
||
Notice that the Major Second
intervals are different: there is a Big
Major Second (9/8) and a Little Major
second (10/9). Notice also that normal Pure Major triad is generated by the
harmonics 4, 5 and 6, while Pure Major Second triad is generated
by the harmonics 8, 9 and 10.
This triad is a
bit more “dissonant” than normal major triad, but is still quite “consonant” to
allow the construction of new scales, by transposing the Major Second triad by some factors chosen by the composer. Notice
also that, in this case, we have to use pure intervals, because tempered
intervals would sound much more dissonant.
3.2
Considerations about the Western Tradition
Classical school
of music has been considered the only point of reference to make music for long
time. Almost all of popular music has also a lot in common with the rules of
classical tradition. Even nowadays, most people unconsciously consider it the
only way to make music. Music that doesn’t follow these rules is commonly
considered non-music. But I believe there could be new ways to develop and
evolve classical rules, as well as starting from different and completely new
paradigms. One of the limiting factors of classical school is stressing the
pitch parameter, to the disadvantage of other sonic parameters, such as timbre,
spectral distribution, accumulation, sonic density, spatialization, etcetera.
On the other hand, with acoustic instruments it is very complicated to write
music which uses these new parameters. But new fields are now opened by the
computer. Also, the concept of note is not the only possible musical paradigm.
Actually, even a single note conceal an extremely complex and subtle structure
that often is not considered by the composer, but it is by the interpreter. I
will treat this argument in next sections.
3.3 Death and
Rebirth of Phoenix: New Musical Paradigms
The acoustic and
aesthetic researches of the second half of 20th century,
demonstrated that structure of acoustic sounds is by far more complex than it
was previously believed. First approaches of electronic music in the Fifties
(Stockhausen et al.) attempted to create sounds starting by scratch, and, at
first, it was believed that electronic media of that time (analog oscillators)
could be able to synthesize any kind of sound, including acoustic sounds. But,
very soon, electronic composers discovered that this goal was impossible, at
least with the oscillators and filters of that time.
3.3.1 The
inner structure and evolution of a sound
The reason of
such difficulty was that acoustic sounds were too complex. Actually, in pitched
instrumental sounds, each harmonic has its more or less independent amplitude
evolution, as well as the evolution of pitch deviation with respect to
theoretic harmonic frequency. What were possible to synthesize by scratch, at
that age, was only sounds sounding very electronic and mechanic (i.e. beeps and
artificial-sounding noises). An acoustic sound contains an independent envelope
(both for amplitude and pitch) for each partial, and global average envelope
can be commonly divided in four phases: 1) the attack transient, that very often contains noisy components (so it
is not possible to represent this phase only with harmonics, for example, the
noise of the piano hammer beating on the string), 2) the decay transient (for example, the initial amplitude decay of a
piano or guitar note), 3) the sustain
phase (in which variations of amplitude and pitch are less evident than in
previous phases) and 4) the release
transient (in which the amplitude of sound returns to zero, at the end of the
note). This scheme is very rough and cannot be applied to all acoustic sounds.
Another factor
that influences and highly increases the complexity of acoustic sounds is the
interpretative gesture of the performer. For example, a violinist can use vibrato
differently even during the evolution of the same note (by continuously varying
vibrato’s amplitude and frequency according to his interpretative feelings). A
clarinetist could completely vary the timbre of the note by modifying lips
pressure and breath flow. So, each played note is always different from the
others, even if, in the score, they should have the same pitch. Actually, a
single note could be considered a musical piece in miniature.
Several computer
music composers have taken into account this fact in their work. Actually the
common “note” concept is somewhat limited when treating of computer music, and
generative processes cannot be applied to the generation of notes only, but
also to the evolution of single notes. In extreme cases, a complete piece could
be made up of a single note, even if the “note” term could not be appropriate
in this case.
3.3.2 Events:
extending the concept of Note
generative music
has often to deal with evolution and processes. Evolution concept implies
gradual and continuous things, while the traditional “note” concept, according
to which notes are a sort of Lego
pieces to be assembled by the composer, implies solid, discrete and stepped
things. However, a real performed note is not so “solid”, as I told above, it
can be compared more to “Plastiline”
than to a Lego brick. Computer music
tools allow to use the “Plastiline”
to mould sounds, by means of evolving parameters that continuously change the
configuration of a single note. So, a computer music sound can be more than a normal note (for example, it
can be made up of a changing cluster of micro-notes), so the “note” term is not
appropriate anymore, I prefer to use the event term. So, generative process
can be applied to the evolution of a single event, besides to the generation of
many events.
4. Some Generative Methods
applied to Music
In the following
sections some methods to generate acoustic material with the computer will be
presented. They can be very simple, such as, for example, applying pseudo-random values generated by the
computer directly to an arbitrary parameter of notes (for example to pitch or
rhythm) or more clever, such as modifying random
distribution, differential
methods, and deterministic algorithms of various kind.
Whatever kind of
algorithm or method is chosen, the main compositional act is parameter
mapping. A very simple algorithm can produce good results with a shrewd
mapping, whereas even complex and sophisticated algorithms can produce bad
results, if parameter mapping is not so clever.
I remember that pitch and duration are only two of the possible musical parameters that
composers can manipulate during music creation, even if they have been by far
the most important compositional parameters for centuries, in western
tradition. One of possible reasons of this predominance, is that note pitch and
duration are the easiest parameter to be represented in a musical score. So, in
the following sections, I assume that the generative methods which will be
applied to pitch and duration, can also be applied to any other sound
parameter.
4.1 Random
numbers
Almost all
computer languages implement a pseudo-random number generator. Normally, the
random generator function implemented in most languages produces integer
numbers within the range of 0 to 32767 or floating-point numbers within the
range of 0 to 1. Pseudo-random numbers are the first and perhaps the most
important generative approach.
4.1.1 The
most simple Generative Process: generating Random Notes
The first
operation one have to do for generative application, is to scale the range of
random numbers to a useful interval, depending on the context. For example, if
we want to apply such numbers to pitch, human range of audibility being
approximately 20 - 18,000 Hz, we have to multiply each random-generated number
by an appropriate factor, then add an offset value, in order to make the lower
bound of range to coincide with desired value. Obviously, 20 - 18,000 Hz is the
range of audibility, not the range of musically useful base pitches of notes.
So we have to reduce this range by an adequate amount (depending on composer
taste).
General formula to scale and translate the
original range to another range, according to minimum and maximum values, is
the following: ![]()
where ScaledValue is the result, CurrentValue is the original random
number (which must be within the range of
0 to 1, so it should be previously scaled to this interval, in case the
random generator of the used language implements a different range), Min is the lower bound of the required
range, and Max is the upper bound.
Applying scaled
random values to the frequency of notes directly in Hertz, produces a brute and
rough result when listening (even if it could be effective in some situations).
A method to slightly improve hearing quality is to map random value to a
musical scale (that can be chosen by the composer). In this case the absolute
frequency of each grade of the scale can be mapped into a table (i.e. a
computer array) and the random numbers should be used as indexes of this table.
Instead of storing absolute frequency values into the table, it is possible to
store the multiplier factors of each grade of the chosen scale. So, base
frequency can be freely transposed, even during the performance, keeping
melodic intervals between notes intact.
4.1.2
Introducing Hierarchical Structure
As it was said
before, music is often compared to a language, with its own grammar and syntax.
Structure of spoken languages is organized hierarchically, as well as structure
of most music. Often, in conventional composition, melody is divided into
sections, similarly to sentences, phrases, paragraphs and words. Each section
is made up of notes or sub-sections, and each group of notes is organized
according to some musical logic. It is expected that the listener should be
able to follow this logic, at least partially, otherwise emotional
communication cannot reach its destination. By the listener’s side, musical
logic is made up of the perception of acoustic and emotional tensions/extensions,
organized in a dynamic process. For example, the Classic Sonata form was made up of two antithetical themes in the
first section that interact each others in second section, to reach a
reconciling synthesis in the third (and final) section. Each one of these main
sections is subdivided into many other sub-sections. Many new elements of
musical logic have been introduced during the centuries, often merged with old
ones, often disowning past styles. Some ways to organize structure in generative
music will be presented below.
4.1.3 Varying
Random Ranges continuously (Tendency Masks)
Even if
generated values are mapped into musical scales, a pure random approach is
still quite rough and trivial to our ears; it appears quite boring after only
few seconds. The problem is that the melodies generated by the uniform random distribution (that is the
type of statistical distribution implemented in most random generator functions
of computer languages) seems to have no logic other than equally distributing
the probabilities that any expected event can take place in any moment. In this
case, any kind of melodic interval could appear, even intervals extremely
large, providing unnatural structure to the melodic line. A way to control and
limit the size of melodic intervals, is to provide tendency masks, i.e.
varying continuously both upper and lower bound of possible random values
generated by the computer.
Continuous
variation of these bounds can be done at least in three different ways: 1]
structured by the composer in a score, 2] varied by the interpreter during a
real-time performance by means of gestural actions on computer devices (for
example, mouse, joystick or graphic tablet) and suited programs, or 3] by means of random (or algorithmic)
sequences of values generated by the computer itself, sampled at a rate lower
than note-generation rate. In the third case, at least two random generators
are present, displaced according to a hierarchical structure: the note
generator and the mask-bound generator. Mask-bound generator should generate a
break-point every n-notes, where n itself can be varied by the
composer/performer as well as be randomly generated. Also, linear (exponential,
or cubic spline) interpolation
between break-points can be provided in order to make tendency-mask transitions
continuous. For example, Granular
synthesis can be classified as belonging to any of the three previous
cases. This kind of synthesis, is not only a sound timbre generation method,
but also a real compositional method, according to the rate grains are
generated, i.e. grains generated in a very fast way seems to produce a single,
fat sound, whereas, with slower rates, each grain seems to be a different note,
randomly generated according to eventual higher-level tendency masks provided
by the composer, or generated algorithmically in turn.
4.1.4
Modifying Random Distributions. Differential approach
Another way to
“break the symmetry” of uniform random
distribution, is to use other random distributions. When using a
distribution different for the uniform one, not all expected values have the
same probability to take place. This approach already provides a “shape” or a
“color” to the total set of generated events. This method produces results more
interesting than uniform distribution, but its efficacy highly depends from the
type of distribution used. Besides all scientific canonical distributions (for
example, Gaussian, Poisson, Cauchy etc.) it is possible to create new distributions by scratch
(some new opcodes of the synthesis language DirectCsound
provides this feature), for example by defining its probability histogram by hand or by generating it algorithmically.
When generating
melodies, it is often more important to define the relation between previous
and next note, than defining their absolute pitch, keeping out of the context.
Defining the interval between two adjacent notes of a melody, is a differential
approach. In this case, random generator doesn’t generate the pitch of each
note directly, but it generates the distance of next note from the previous
one. One important peculiarity of differential method is that each generated
event depends not only from the random number itself, but also from the value
of previous event. This can provide unity, efficacy and originality to the
melodic line, if mapping and distribution choices are done shrewdly.
Differential approaches can also be applied to note duration and rhythm.
Another method
that derives from differential approach, is to use the Markov chains. In Markov chains, the probabilities of the newly
generated value not only depend from a single previous value, but from a set of
n
previous values where n is the order of Markov chain. For
example, when n = 2, newly generated value depends only from the immediately
previous one (as in the case of differential approach); when n is bigger than
2, newly generated value depends from the last n - 1 values.
4.1.5
Sections of Musical Speech
Melody sections
can also be generated by means of random numbers. In this case the composer should
provide collections of syntactical rules for each section to be generated. For
example, a melodic sentence could be made up of two or more phrases, the first
phrase being in opposition with the other ones. A set of both rhythmic and
melodic templates should be provided in order reach this goal, and the random
generator should choose the correct collection of templates for each section.
For example, each template collection can contain only pitches belonging to
some determinate class of chords, and/or pitches used as connection between
grades of such chords. Obviously, new rules can be created from scratch by the
composer or by the algorithm itself with genetic or evolutionary methods. In
some case, rules can be made up of both random methods and deterministic
algorithms.
4.2
Algorithmic composition in Generative Music
Random
generation is subject to refinedly be adjusted by the composer, in order to fit
very subtle compositional aesthetics, by means of the methods I mentioned
before. However, other non-random methods can also be applied to generative
music, such as algorithms of various kind (mathematical functions, fractals,
cellular automata, neural networks, genetic algorithms, evolutionary processes,
digital sampling of natural signals, physical phenomena simulations, bitmap
image scanning, etcetera). Going into details is not the intention of this
paper, so I will just present some arbitrary and trivial example.
4.2.1
Mathematical functions
A mathematical function,
such as, for example, a trigonometric function can be chosen to generate global
shape of some musical control parameter. In the most simple case, a sinusoid
having sub-audio frequency can be sampled at different times, and sampled
values can be applied, for example, to note pitch (generating the melodic line
in this case), rhythm, or amplitude. Note articulation could be defined from
another trigonometric function. Obviously, in the case of a fixed sinusoid,
resulting music could be very repetitive and boring, but composer could take
high-level control on the sinusoid, by vary its amplitude and frequency.
Sinusoid’s amplitude will vary the interval range of melody generated, while
the variation of sinusoid’s frequency will vary the length of each melodic
phrase. Waveforms other than sinusoids can be chosen to make the result more
complex, and other methods of shaping
these waveforms (such as non-linear
distortion and wave-shaping) can
be added to make it more interesting and varied, such as clipping (continuously varying the clipping points themselves,
according to other mathematical functions) or wrapping the signal around. Obviously the sampling values of
generated signal could also be mapped according to a map carefully provided by
the composer, before they are applied to the musical parameters.
4.2.2
Fractals and Cellular Automata
Fractals, such as Mandelbrot set,
not only can be applied to generate images of fascinating beauty, but also to
generate algorithmic music. For example, to generate an image with the Mandelbrot set, one have to select the
coordinate range of the region of interest on the complex plane, as well as
image resolution, that is the number of pixels for both width and height. Then
apply the recursive formula: ![]() where c
is a complex number whose real and imaginary parts are the coordinates of
points belonging to the complex plane area we take into account. The iteration
cycles of recursive formula are stopped when the absolute value of x
exceeds 2, or when the number of
iterations exceeds a limiting threshold set by the user. The iteration
tests are repeated for each pixel of the area; the output data (for each pixel)
is the number of iterations required to reach (or to exceed) 2.
Output data are normally mapped to a color set provided by the user.
where c
is a complex number whose real and imaginary parts are the coordinates of
points belonging to the complex plane area we take into account. The iteration
cycles of recursive formula are stopped when the absolute value of x
exceeds 2, or when the number of
iterations exceeds a limiting threshold set by the user. The iteration
tests are repeated for each pixel of the area; the output data (for each pixel)
is the number of iterations required to reach (or to exceed) 2.
Output data are normally mapped to a color set provided by the user.
A method to
apply Mandelbrot set to music, is to consider single points of the complex
plane and take their number of iteration. Scanning of points can be done
linearly (horizontal or vertical lines can be serially analyzed and the results
of each point can be displaced in subsequent variation of a musical parameter,
such as, for example, pitch of notes) or a custom path can be provided by the
user, for example an orbit or a curve of any shape. Several horizontal lines
can be scanned in parallel, by assigning their output to a different voice,
obtaining polyphony. In this case, time interval of point scanning should be
constant. Obviously, output values, that are integer numbers, can be mapped in
any sorts of ways by the composer.
One-dimensional Cellular
Automata can be easily applied to music. One-dimensional cellular
automata are made up of a single row of cells (i.e. memory locations, in
computer implementations), having an initial state (number contained in each cell),
that interact with the adjacent cells, according to a rule given by the user.
Next state of each cell is determined by its previous state and the state of
previous adjacent cells. With this simple process, interesting structures are
generated, in which a sort of auto-organization often emerges. Cellular
Automata data can be mapped in many ways for musical tasks, for example, one
can consider the state evolution of a single cell to control melodies or
rhythms; it also possible to consider an entire row of cells controlling the
amplitude of a bank of oscillators, making it possible to control additive synthesis. In this case,
composers can arbitrarily choose frequency mapping of each oscillator of the
bank. Other more subtle mapping is possible by adding some hierarchy to the raw
data, for example, by choosing melodic phrases according to data values,
instead of single notes, such phrases being previously generated by the same or
by another cellular automata process.
4.2.3 Bitmap
images
A bitmap image
is made up of a set of points, named pixels, each one of that containing
its color information. Normally, the color of each pixel is divided into three
components, whose values express the intensity of red, green and blue colors. So the mix of various
combinations of these three colors provides the viewer a perception of almost
any color visible. RGB (Red, Green, Blue)
data can also be mapped to control musical parameters. RGB values are usually codified as a two-dimensional matrix stored
in the computer memory: width and height of the image are the dimensions of the
matrix, and RGB values are its
elements. Usually, each RGB value of
a pixel, is made up of three bytes (or four bytes, when including Alpha
Channel), each byte expressing the intensity of an RGB component. A byte is made up of 8 bit so the value range of
each RGB component is 0 to 255. This
value range can be mapped to control any musical parameter such as amplitude or
frequency. So, image scanning can output a flow of RGB values, and each RGB
value component can be used to control a different musical parameter. A timed
scanning of the vertical lines of the image can be used to obtain a flow of
arrays of RGB components, whose
values can be assigned to the amplitudes of a bank of oscillators, making it
possible to dynamically control additive
synthesis. Frequency mapping of each oscillator (belonging to the bank) can
be arbitrarily chosen by the composer. RGB is not the only way a color can be
expressed. An RGB value can be easily
converted to HSV (Hue, Saturation,
Value) or HSL (Hue, Saturation,
Luminance) coding. The difference between these two way of coding is that
in HSV the Value component
represents the maximum component value between corresponding RGB components, whereas, in HSL,
Luminance represents the sum of RGB components. For humans, I believe that HSL provides a more direct and intuitive representation of
perceived colors. HSL is even easier
to be applied to musical parameters. For example, Luminance is quite straightforward related to sound amplitude, Hue can be easily interpreted with
timbre, and Saturation could be
applied, for example, to spectral energy distribution.
Generating music
starting from bitmap images opens a huge field in both generative and
non-generative music. In fact the image can both be drawn by the composer (the
image being in this case a sort of graphical score) and be produced by any
generative method that can be applied to computer graphics. For example fractal
images can be easily converted to music. Furthermore, scanning a bitmap image
(to get its data, which have to be transformed in musical parameters) can be
done linearly (for example, from the left to the right positions of the image),
as well as non-linearly, following any possible path (for example, forward-backward,
up-down and down-up, circular, elliptical, spiral paths and so on), paths can
either be generated algorithmically or be covered by the performer with an
interpretative gesture. All these possibilities open new paradigms for musical
performances, transforming music into a sort of architectural construction to be explored. This concept will be
expanded with the Hyper-Vectorial Synthesis, a technique described in next
sections.
5. Musical Travels in
Space and Time: Hyper-spatial Music
Music is an art
displaced in the time domain, and its representation is normally provided by
means of two-dimensional sheets of
paper in the form of a semi-graphical score. A graphical score represents time
by means of a spatial dimension. The other spatial dimension of a score is
frequency. However, relation between musical space and time contains several
further aspects.
5.1 Space Ű Music relations
Evolution has
provided humans with a very precise recognition of the displacement of a sound
source, as well as with the capability to recognize the size and the shape of
the environment a sound source is placed in. But besides spatial recognition,
there are other Space/Music relations
such as the Compositional Space. Compositional Space is an imaginary space
concerning the structure of a music composition. This space presents several
organization levels, from the micro-level to the macro-level and is subjected
to be analyzed with a set-theory approach, actually this is the model used by
most musicologists and music-analysts. As it was said before, musical time can
be treated as a spatial dimension. Traditional western music-writing system
uses the concept of “note” to deal with this kind of space in music notation.
However the “note” concept runs into a lot difficulties when dealing with a
compositional space of more than two dimensions (pitch-time). Computer music offers the scope of notes having
much more than pitch and time as parameters. Even if spectral evolution of a
sound signal can be completely represented into a three-dimensional Cartesian
space expressing frequency-time-amplitude, nevertheless sound generation can
involve a huge number parameters. Dozens of further parameters can be assigned
to single event. This opens the door to hyper-spatial world representing music.
Sound-synthesis computer languages (such as Csound)
can handle any number of sound parameters per event, by means of its
orchestra-score philosophy. Besides duration, amplitude and pitch, each event
can be activated with an arbitrary number of additional synthesis parameters,
depending on the way a synthetic instrument is implemented. For example, an
instrument containing 20 different controllable parameters can be represented
in a space having 20 dimensions. The problem is how a single performer can control
such massive amount of parameters, in the case of complex instruments. VMCI
Plus, a program whose purpose is to control DirectCsound (a realtime
version of Csound), provides this
control by introducing two kinds of spaces interacting each-others: motion space and sonic-parameter space. Interested people can download these
programs from my web site.
5.2 Traveling
Forth and Back inside Space and Time
Computer Music
provides tools to play a soundtrack at different rates, slowing down or
accelerating reading speed without altering the original pitch (this can be
obtained by means of spectral techniques such as Phase Vocoder, or with
time-slicing tools such as Granular Synthesis). It is also
possible to completely stop or to scan backward the temporal flow of a recorded
sound, a sort of slow-motion film-editing machine, applied to music. On the
other hand, it is also possible to keep temporal flow constant and traveling in
the frequency domain, the other main dimension of sound signals, so,
transposing a sound signal without altering its duration and spectral-energy
distribution is also possible. This opens huge fields to composers, but even
more interesting and intriguing is to explore a sound signal or a compositional
structure interactively. I theorized this kind of travels in the article “Exploration of a Virtual Sound System”
(1989), in which a performer (named Composinterpreter)
drove a sort of musical spaceship. A technique to make this kind of travels possible
has been introduced and continues to be developed: the Hyper Vectorial Synthesis.
What is interesting and new is that the Hyper
Vectorial Synthesis non only allows to explore the two standard dimensions
of a sound signal (time-frequency), but also other dimensions belonging to Compositional Space, such as
interpretative parameters and generative creation processes.
5.3
Conducting a Hyper-Spatial Spaceship for Musical Travels
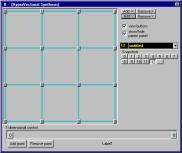
|
Fig. 3
Hyper-Vectorial-Synhtesis |
The Hyper Vectorial Synthesis technique is
currently implemented in VMCI (Virtual Midi Control
Interface) a computer program that provides a user interface to voyage in Compositional Space. It consists of a
two-dimensional matrix containing several points called “breakpoints” (these that
are visible in a rectangular area of computer screen as numbered buttons). Breakpoints are placed inside a
rectangular area, and each breakpoint
represents a vector containing the values of several synthesis parameters, so
each breakpoint actually makes up a
sound timbre configuration. A punctiform focal cursor is moved inside the
rectangular area, dynamically changing its position, according to a path
generated algorithmically (for example, an orbit) or by means of a user gesture,
and the result of this action is to output a vector of parameters, that are
sent to a sound-synthesis engine (such as DirectCsound).
Such parameters are calculated depending on cursor position, starting from the
weighted average contents of the four nearest breakpoints to the cursor. So output vector values dynamically
change too, according to the motion of the cursor.
If we compare a
synthesis parameter to a dimension of an n-dimensional space, we can consider
a sonic configuration as a determinate point of that space. If a synthesized
sound changes its timbre continuously, we can compare that sound to a point
moving inside the corresponding n-dimensional space. The number of
dimensions of that space is determined by the number of variant synthesis parameters.
For example, a synthesized timbre in which only two synthesis parameters are
adjustable by the user (for example the canonical pitch and amplitude), can be
considered as a point of a two-dimensional space, i.e. a point of a plane area.
Until now, the
compositional configuration of most western music is practically based on a
two-dimensional plane area, because only pitch and time displacement of sound
events can be written in a standard music score (amplitude of notes can be
considered as a third dimension, but standard western music notation system
doesn’t allow to define this parameter with precision). Computer music opens
the possibility to compose with any number of discrete or continuous variant
parameters, making it possible to deal with a hyper-spatial musical paradigm.
One of the goodies of this technique, is that it can be applied not only to
timbrical parameters of a synthesized sound, but also to any parameter of
algorithmic composition (even if, in computer music, timbre evolution already
is a compositional parameter, and there isn’t a clean distinction between
timbrical and structural processes), or to any parameter which controls the
generative process.