Complexity and Fractal Dimension

in 26 Mesoamerican Pyramids

Dr. Gerardo Burkle-Elizondo, Ph-D

Universidad Autónoma de Zacatecas. Unidad de Postgrado II.

Doctorado en Arte y Humanidades. Ave. Preparatoria s/n.

Col. Hidráulica. CP 98060, Zacatecas Zac. México.

E-mail: burklecaos@hotmail.com

Prof. Nicoletta Sala, Ph-D

Accademia di Architettura (Academy of Architecture) di Mendrisio.

Universitá della Svizzera Italiana (University of Lugano).

Largo Bernasconi , 6850 Mendrisio. Switzerland.

E-mail: nsala@arch.unisi.ch

Abstract

Mesoamerica is a region that comprises Mexico and upper Central America and where developed a civilisation after about 1400 BC. The Mesoamerican civilisations constructed numerous administrative and ceremonial centres and erected numerous monuments. These reflect astronomic knowledge and expertise in numeration and calendars. Mesoamerican Pyramids are symmetric stable architectural forms that had resisted successfully the course of time. More often they were built as a four-sided form with stairs in one side almost always, and generally supporting a temple at the top. Pyramids had a religious function and were associated with some god, fertility or war cult. They were related too with a sacred mountain like a way to make contact with the under and upper world (Tlalocan and Tamoanchan), and in the Maya case at Palenque and other places we can see a temple dedicated to an ancestor raised over his tomb. Other pyramids like at Chichen Itzá were dedicated to celebrate the coming and end of time periods. The holy landscape is usually inside the jungle or natural environment like a dynamic and harmonic unit. The aim of this paper to show the results of a complex and fractal analysis which has involved 26 Mesoamerican pyramids; 17 belongs to the Maya culture and 9 to the Aztec and Mixtec cultures. In agreement to recent studies connected to determine the complexity in the arts and architecture, the images of the different Mesoamerican pyramids were scanned and analysed to calculate Box, Information and Mass Dimension and the log-log plots graphs. Final results evidenced high levels of complexity in Mesoamerican pyramids connected to their symbolism.

1. Introduction

The Mesoamerican civilisations realised numerous administrative and ceremonial centres and erected numerous monuments (for example, pyramids and tombs), that reflected astronomic knowledge and expertise in numeration and calendars.

Mesoamerican Pyramids are symmetric stable architectural forms that had resisted successfully the course of time, as shown in figure 1. The symmetry is used in different architectural styles and through the centuries [1, 2].

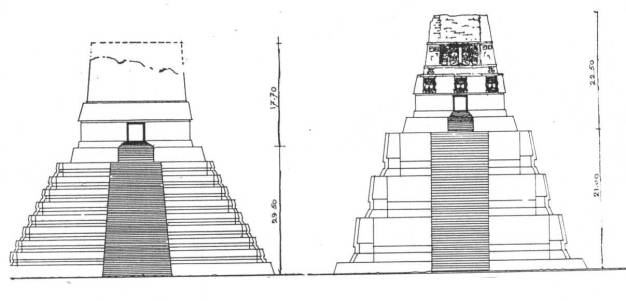
Figure 1 Mesoamerican Pyramids evidence symmetric architectural forms (Temples I, and II of Tikal)

More often the pyramids were built as a four-sided form with stairs in one side almost always, and generally supporting a temple at the top. Pyramids had a religious function and were associated with some god, fertility or war cult [2]. They were related with a sacred mountain like a way to make contact with the under and upper world (Tlalocan and Tamoanchan), and in the Maya case at Palenque and other places we can see a temple dedicated to an ancestor raised over his tomb. Other pyramids were dedicated to celebrate the coming and end of time periods. For example the pyramids located at Chichen Itzá. The holy landscape is usually inside the jungle or natural environment like a dynamic and harmonic unit. The aim of this paper is to introduce a research that analyses the complexity of the Mesoamerican Pyramids using the Fractal dimension. The paper is organized as follow: in the section 2 we present the complexity and fractal geometry and their applications in architecture. The section 3 describes our research and the results. In section 4 there are the conclusion and the section 5 is dedicated to the references.

2. Complexity and Fractal geometry in architecture

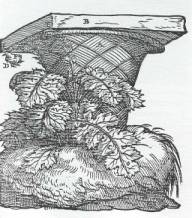
For many centuries architecture has followed the Euclidean geometry and Euclidean shapes and we are not surprise to observe that the buildings have Euclidean aspects. On the other hand, some architectural styles are informed by Nature, and much of Nature is manifestly fractal and complex. o perhaps we should not be so surprised to find fractal architecture. As we shall see, fractals appear in architecture for reasons other than mimicking patterns in Nature. Figure 2a shows a Vitruvius’s draw that describes the creation of the first Corinthian capital. Figure 2b illustrates a Corinthian capital.

a) b)

Figure 2 The creation of the Corinthian capital a) and a real Corinthian capital b)

The Fractal analysis in architecture can be divided in two parts [3]:

· on a little scale analysis (e. g, to analyse the single building shape);

· on a large scale analysis (e.g., to study the urban growth using a fractal point of view) [4, 5].

In the little scale analysis we can observe:

· the box-counting dimension (to determine the fractal dimension of a design to use this parameter as a critical tool) [6, 7];

· the building's self-similarity ( e.g., a building's component which repeats itself in different scales) [3]

· urban building generation using fractal algorithms [8, 9].

Figures 3, 4 and 5 show three examples of self-similarity in the Chinese architecture, in Mesoamerican architecture, and in Hindu architecture respectively. Figures 6 and 7 illustrate two fractal organisation in African villages [10].The same shape is repeated in different scales.

Figure 3 The Hall of Prayer for Good Harvest (Temple of Heaven: “Tiantan”) Beijing (China). It is an example of self-similarity in the Chinese architecture. Tiantan, the Temple of Heaven, was established in 1420 during the reign of Ming Emperor Yongle (1403-1424).

Fractals are self-similar because every smaller piece of the objet, resemble the larger pieces and the whole depends on the resolution used to make the measurement, and this produces a scaling relationship that depends of a power law. This property means that the Dimension is a measure of scaling and self-similarity. The Fractal Dimension Fd shows the way many additional smaller pieces of an object are revealed when it is magnified and analysed in another and fine resolution. This object fills up space, and it give us information about area, length, form and volume. A data series and a time series can also be fractal when it has self-similarity because describes how small changes in the values measured in short time or amount values, are related to large variations over long time.

Figure 4 Self-similarity in Mesoamerican architecture (El Castillo, Chichen Itzá)

Figure 5 Self-similarity in Hindu architecture

Figure 6 Fractal organisation in African village (Ba-ila, Zambia) [10, p. 27]

Figure 7 Fractal organisation in African village (Mokoulek, Cameroon) [10, p. 30]

3. Complexity in Mesoamerican Pyramids: Our approach

The aim of our work is to study the Mesoamerican pyramids’ structures trying to find out the patterns and designs and the forms into this complex geometry that appear to enclose a specific guide of information encode in them [7, 11, 12]. What we want attempt is to decipher the possible interconnected nature of different reckoning systems. To realize our research project we have established three different procedures of analysis. The first one studies the structures like series from the point of view of areas against volumes. In the second procedure we visualize the pyramid like the reason of the volume interpolated with its empty complement mould. The third one is the calculation of the fractal dimension of a big number of pyramids using the Box counting method that shows rather the roughness of an object or fluctuations of the height over length scale. In the past we found out those Mesoamerican artworks, sculptures and architecture have fractal dimension

The present study has special interest to analyse the interrelationships that in the past existed in Mesoamerica between the art, the architecture of the cities, the religion, the nature, the society, the cosmos vision and the empire, all these related to a ceremonial center. The problem in the history and the proofs we have belongs to these three categories:

1. geographic-ecological,

2. sociopolitical,

3. symbolic.

In the last one we have to consider the idea of a “sacred space”, integrated by the architecture, the nature, the social order that includes the ritual practice and the symbols included in the ceremonial complex that contains the buildings, the artistic manifestations and the ritual it self.

We have to consider that the cities plays a major role in the organization of the society and the government to have the control at the same time in a sacred way. These ceremonial capitals, some times monumental, were utilized like political technical to get authority articulating the myth, the military policy, and the economic order using an space erected on a grandiose scale, an image of the cosmos, of a time able to give motion to the empire and the power and structure to the activities in an organising principle based in the art, the architecture and symbolic details.

In our approach we selected 26 Mesoamerican pyramids, we digitised their high resolution images and using the program Benoit^TM we calculated: the Box (Db), the Information (Di), and the Mass Dimensions (D_M). Figure 8 shows an example of Log-log plot for “Tikal I” pyramid

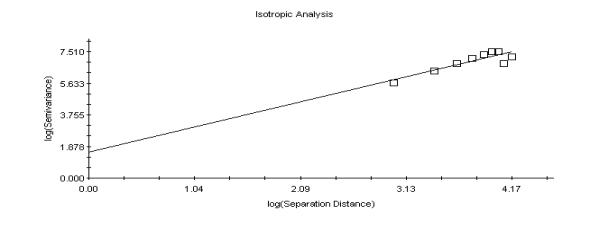
Figure 8 Log-log plot for "Tikal I" studied with Model Volume-Empty Complement. (Fractal Dimension 1.28). The fractality can be appreciated as a straight line.

In the table 1 we can observe the results of the Fractal Dimension values that we obtained in each of the three procedures.

Table 1

PROCEDURES AND METHODS TO STUDY THE FRACTAL DIMENSION OF MESOAMERICAN PYRAMIDS
	FRACTAL DIMENSION METHOD Df (BENOIT)			DIMENSION Dv FROM PROCEDURES 1 and 2
PYRAMIDS	BOX DIMENSION (Db)	INFORMATION DIMENSION (Di)	MASS DIMENSION (Dm)	VOLUME - EMPTY COMPLEMENT (Dv)	S AREAS - S VOLUMES (Dv)	SEG - MENTS
Templo V Tikal	1.940	1.937	1.9540	1.223	1.4950	14
	± 0.016	± 0.003	± 0.086	± 0.206	± 0.339
				r^2= 0.835	r^2= 0.735
Templo I Tikal	1.925	1.951	1.995	1.286	1.204	12
	± 0.019	± 0.0009	± 0.173	± 0.264	± 0.037
				r^2= 0.772	r^2= 0.993
Templo III Tikal	1.928	1.924	2.016	1.341	1.113	12
	± 0.014	± 0.002	± 0.020	± 0.176	± 0.028
				r^2= 0.879	r^2= 0.996
Piramide Uaxactun E-VII	1.941	1.950	1.938	1.171	1.193	8
	± 0.005	± 0.001	± 0.013	± 0.122	± 0.069
				r^2= 0.929	r^2= 0.977
Templo de las Inscripciones Palenque	1.922	1.938	1.936	1.117	1.157	12
	± 0.011	± 0.001	± 0.011	± 0.079	± 0.038
				r^2= 0.966	r^2= 0.992
Templo del Sol Palenque	1.933	1.936	1.925	1.181	1.310	14
	± 0.007	± 0.002	± 0.180	± 0.114	± 0.078
				r^2= 0.938	r^2= 0.976
Templo Mayor de Cempoala	1.932	1.947	1.917	1.221	1.100	20
	± 0.005	± 0.002	± 0.043	± 0.113	± 0.029
				r^2= 0.936	r^2= 0.994
Xpujil (Torre Lateral Sola)	1.933	1.939	1.948	1.238	1.113	13
	± 0.013	± 0.005	± 0.007	± 0.118	± 0.026
				r^2= 0.940	r^2= 0.996
Yaxchilan Estructura 30	1.934	1.955	1.973	1.277	1.317	13
	± 0.020	± 0.001	± 0.035	± 0.197	± 0.081
				r^2= 0.857	r^2= 0.974
Piramide Monte Albán Edificio M	1.934	1.934	1.932	1.146	1.266	10
	± 0.010	± 0.001	± 0.015	± 0.106	± 0.099
				r^2= 0.944	r^2= 0.959
Piramide de Edzná Campeche	1.938	1.955	1.960		1.101	6
	± 0.010	± 0.001	± 0.066		± 0.030
					r^2= 0.997
Piramide 364 Nichos Tajin	1.926	1.910	1.927	1.100		8
	± 0.007	± 0.002	± 0.003	± 0.166
				r^2= 0.879
Piramide Calixtlahuaca Adoratorio Ehecatl	1.924	1.945	1.948	1.224		8
	± 0.008	± 0.002	± 0.025	± 0.166
				r^2= 0.872
Piramide de Cholula	1.941	1.964	2.001	1.172		9
	± 0.003	± 0.001	± 0.053	± 0.167
				r^2= 0.875
Templo IV Tikal	1.940	1.957	1.944	1.212	1.100	12
	± 0.011	± 0.0008	± 0.013	±179	± 0.013
				r^2 = 0.868	r^2= 0.999
	FRACTAL DIMENSION METHOD Df (BENOIT)			DIMENSION Dv FROM PROCEDURES 1 and 2
PYRAMIDS	BOX DIMENSION (Db)	INFORMATION DIMENSION (Di)	MASS DIMENSION (Dm)	VOLUME - EMPTY COMPLEMENT (Dv)	S AREAS - S VOLUMES (Dv)	SEG - MENTS
Castillo Kukulcan Chichen Itza	1.920	1.904	1.909	1.210	1.190	10
	± 0.009	± 0.003	± 0.038	± 0.173	± 0.075
				r^2 = 0.875	r^2= 0.973
Templo I Tancah	1.935	1.958	1.945		1.131	14
	± 0.022	± 0.0009	± 0.006		± 0.031
					r^2= 0.994
Torre Gran Palacio Palenque	1.935	1.945	1.948		1.639	9
	± 0.012	± 0.002	± 0.007		± 0.373
					r^2= 0.506
Templo de Tlahuizcanpantecuhtli en Tula	1.942	1.941	1.937	1.488	1.346	11
	± 0.006	± 0.002	± 0.005	± 0.294	± 0.388
				r^2 = 785	r^2= 0.632
Piramide de Quetzalcoatl Teotihuacan	1.937	1.946	1.952
	± 0.006	± 0.002	± 0.010
Observatorio Chichen Itza	1.927	1.943	1.894
	± 0.009	± 0.003	± 0.010
Templo del Sol Teotihuacan	1.923	1.913	2.000
	± 0.004	± 0.003	± 0.014
Templo del Adivinio Uxmal	1.908	1.911	2.085
	± 0.006	± 0.0005	± 0.124
Piramide del Dios Descendente Tulum	1.929	1.950	2.085
	± 0.006	± 0.0005	± 0.126
Piramide Huichapa Edificio C	1.937	1.967	1.952	1.158		12
	± 0.020	± 0.001	± 0.006	± 0.107
				r^2 = 0.944
Edificio de las Columnas Mitla	1.928	1.949	1.902	1.236		21
	± 0.004	± 0.001	± 0.004	± 0.116
				r^2 = 0.942
Las Chimeneas Cempoala				1.349 ± 0.268		10
				r^2= 0.760

GENERAL 1.312 ± 0.179 1.236 ± 0.108

AVERAGE 1.931 ± 0.010 1.941 ± 0.0017 1.959 ± 0.042 r² = 0.874 r² = 0.918 11.72

4. Conclusions

We studied the Complexity and we analysed the Fractal Geometry in 26 Mesoamerican pyramids; in 22 we found Fractal Dimension and Fractality with our models and procedures using the s/w Benoit^TM and the GS+ Programs; in other 4 pyramids we found only Fractal Dimension with the s/w Benoit^TM. Most of the buildings could be fractal objects.

Our data analyses on the fractality and the complexity in Mesoamerican architecture could suggest us that the architects of these pyramids tried to imagine some models observing the nature. Basic symbolism representing their cosmos vision are present in the Mesoamerican pyramids related with earth, water and fertility, mountains and caves. All these symbols are the manifestations of a cult system that included not only the cosmology, but the complex mathematics involved in it and in the mythic and the ritual concepts. Mesoamerican architects conceived spatial representations before building a pyramid or other of their monumental works [11]. In our approach we found out some fractal models with self-similarity properties, but it would be speculative to conclude that comparison between our research and the existing pyramids prove that the builders of these pyramids conceived their models using the same structures that we have presented in this work [11].

The complexity of Mesoamerican pyramids and their mathematics connections helped us to suppose the existence of a symbolic model of the universe, that evidences the mythic structures and the scientific development reached, in ancient times, by the Mesoamerican cultures. We presume that this mathematical computation, which worked well for these buildings, reflects the presence of significant numbers and their fractal expressions out of a pure randomness. Our findings lead us to believe in the possibility that, when the architects designed their buildings, they were thinking on the basis of the concept of movement. We can also suppose that Mesoamerican architects imagined and designed their cities and temples with connections to the astronomical data and to the patterns into these massive models [7, 11].

5. References

[1] Stierlin H. (2001), The Maya Palaces and pyramids of the rainforest, Taschen, Köln.

[2] Sala N. and Cappellato G. (2003), Viaggio matematico nell’arte e nell’architettura, Franco Angeli, Milano.

[3] Sala N. (2002), The presence of the Self- Similarity in Architecture: Some examples, Novak M. M. (ed.), Emergent Nature, World Scientific, pp. 273 – 283.

[4] Batty M. (1991), Cities as Fractals: Simulating Growth and Form. In Crilly A. J., Earnshaw R. A. and Jones H. Fractals and Chaos, Springer - Verlag, New York, pp. 43 – 69.

[5] Frankhauser P. (1994), La Fractalité des Structures Urbaines, Collection Villes, Anthropos, Paris, France.

[6] Bovill C. (1995), Fractal Geometry in Architecture and Design, Birkhäuser, Boston.

[7] Burkle-Elizondo G., Fuentes-Larios A.G. and Valdez-Cepeda R.D. (2004), Fractality and Fractal Dimension in Mesoamerican Pyramid Analysis, Novak M.M. (ed.), Thinking in Pattern: Fractals and Related Phenomena in Nature, World Scientific, Singapore.

[8] Saleri Lunazzi R. (2004), Pseudo-urban automatic pattern generation, Chaos and Complexity Letters, 3, pp. 127-138 (in print).

[9] Marsault X. (2004), Generation of textures and geometric pseudo-urban models with the aid of IFS, Chaos and Complexity Letters, 3, pp. 109-126 (in print).

[10] Eglash R. (1999), African Fractals: Modern Computing and Indigenous Design, Rutgers University Press, Piscataway.

[11] Burkle-Elizondo G., Sala N. and Valdez-Cepeda R.D. (2004), Geometric and Complex Analyses of Maya Architecture: Some Examples, Williams K. (ed.), Nexus V Architecture and Mathematics, Kim Williams Book, Fucecchio, pp. 57-68.

[12] Sala N. and Cappellato G. (2004), Architetture della complessità: la geometria frattale tra arte, architettura e territorio, Franco Angeli, Milano.