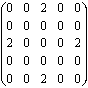CA3D and CA-Tree: Creating virtual objects by using Cellular Automata.

Prof. E. Bilotta.

Department of Linguistics, University of Calabria, Arcavacata di Rende (CS), Italy.

e-mail: bilotta@unical.it

Dr. A. R. Gabriele.

Department of Linguistics, University of Calabria, Arcavacata di Rende (CS), Italy.

e-mail: a.gabriele@unical.it

Dr. M. G. Lorenzi.

Department of Linguistics, University of Calabria, Arcavacata di Rende (CS), Italy.

e-mail: m.lorenzi@unical.it

Prof. P. Pantano.

Department of Mathematics, University of Calabria, Arcavacata di Rende (CS), Italy.

e-mail: piepa@unical.it

Abstract

In the following work we present artistical forms, realized using two software applications that we designed and implemented ad hoc, CA3D and CA-Tree.

The first tool produces fractal structures. Simulating the CA evolution, this software makes three-dimensional patterns, by representing each cell of the CA by a cube of a different colour, depending on its state and on its rule-table. We have called these structures "Fractal Solids".

CA-Tree generates fractal structures utilizing cylindrical forms to represent the cells. In addition, it allows to modify the dimension of the cylinders during the CA evolution. In fact, while in the visualization with cubes their dimensions remain constant, in the visualization with cylinders height and radius vary during the simulation. We have called these structures "Fractrees", considering the characteristic configuration, similar to trees, they show.

Fractal solids and Fractrees can be used in different ways. For example, in virtual worlds and environments, they can represent the objects their form reminds of (pyramids, trees, etc.) or they can be used as units to build other forms (cities, animals, etc.). Some experimentation we have been carried out include all these representations, used to create characters, pictures, stories and videos.

1.Introduction

Cellular automata (CA) were introduced by von Neumann and Ulam as simple models in order to study some biological processes. A cellular automata is a discrete dynamical system, that is, a system in which the variables that determine and describe their evolution (space, time and states) assume discrete values.

Self-replication, the capacity of the cellular automata to evolve reproducing some patterns, is a phenomenon that is extensively investigated [1-4]. In particular, we studied two-dimensional k-totalistic cellular automata [3] that present the self-replication phenomenon [3-5]. In order to investigate comprehensively the obtained spatio-temporal patterns, we implemented the CA3D software, which simulates the evolution of k-totalistic two-dimensional cellular automata. The objects obtained by the simulations present different characteristics, typical of fractal objects [6-8], such as self-similarity and fractal dimension.

These two characteristics are easily identifiable in such objects. The first one is immediately visible, while the fractal dimension has been calculated using the box-counting [6-8] method.

The beauty of these objects and their characteristic forms let us create virtual objects and worlds [9-11].

2. Emerging forms in CA3D

CA3D allows the representation of the evolution of a cellular automata in the spatial-temporal dimension.

The evolution of the automata in time can be represented into the three-dimensional space, adding a third dimension to the cell of the plane, for example using a cube for each cell.

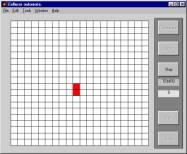
The following figure reports a cellular automaton in its initial configuration (Figure 1.a) and the first steps of its evolution (Figure 1.b).

a

b

Figure 1. : A cellular automaton in its initial configuration (a) and the first six steps of its evolution (b).

The cells are represented as cubes in the space, and positioning the various configurations one above the other, from top to bottom, we obtain the spatio-temporal evolution of the cellular automata.

The next example (Figures 3-4) shows the evolution in space of the initial configuration represented by following the matrix (Figure 2):

a

b

Figure 2. : Initial configuration of the cellular automaton (a) and the matrix it represents (b).

The automata evolves for 31 temporal steps, obtaining the model shown in Figures 3-4.

Figure 3: Three dimensional view of the obtained object

Figure 4: a) and b) show two lateral views of the object; c) and d) report two different views: from below c), and from above d).

The object we obtained have been called Fractal Solids, since they exhibit self-similarity characteristics (Figure 5).

Figure 5: Self-similarity of a Fractal Solid, from a lateral view and in perspective.

CA3D implements a procedure that calculates the dimension of each object that has been evolved using the box-counting method, that in our case is a fractal dimension.

Figure 6: Examples of Fractal Solids. The fractal dimension of the objects is the following:

a=2.7215; b=2.4207; c=2.5042; d=2.9302; e =2.8277; f =2.6684.

3. CA-Tree

Subsequently, a new tool, called CA-Tree, has been implemented, that allows the generation of new fractal structures which make use of different geometrical forms to represent the cells (cylinders rather than cubes). In addition, we decided to modify the dimension of the cylinders during the CA evolution. In fact, while in the visualization with cubes thier dimension remains constant, in the visualization with cylinders height and radius vary during the time steps of the simulation. These structures have been called Fractrees, considering the characteristic configuration they show if we rotate their position upside down. 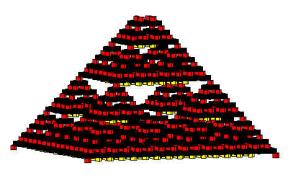Some examples are shown in Figure 7.

Figure 7: Examples of Fractrees.

In Figure 8 two trees obtained introducing a factor of probability to decide the creation of a branch.

Figure 8: Two examples of trees evolved taking into consideration a factor of probability.

4. Artistic applications

Artists have been extensively using, during the last years, new methods and instruments, inspired by mathematical models, to generate artistical and creative forms, as well as artificial worlds, through which new experimentations can be carried out and cultural products of high expressiveness can be created. ESG group creates images, sounds and videos using mathematical models related to complexity, chaos and artificial life, among the others [9-10]. In addition some experiments of storytelling have been carried out: one of it represents the evolution of a robot and the exploration of artificial worlds, made by different configurations of one- and two-dimensional cellular automata. The sound track was also created starting from one- and two-dimensional cellular automata. [11]

In the poster (Figure 9) characters, landscapes and other objects are realized using one and two-dimensional cellular automata. In particular, a city landscape has been created, using gliders as buildings and virtual trees, created respectively using CA3D and CA-Tree (bottom). All the elements of the composition (Figure 10) are then illustrated separately, showing the one or two-dimensional CA the are generated from (center). From the top, the evolution steps of a Fractal Solid, created using CA3D, fades into the generated form; the same form is visualized, upside down, with CA-Tree. Scientific references, which are at the basis of these results, are illustrated on the sides. All the poster is generated following a metaphor: the evolution of the forms in time steps, and their subsequent superimposition, to arrive to the complete (flattened) composition. Some characteristics of the mathematical models that have been used are present in its logic of composition: for example, the same object is present at different scales in different points. Finally, all the elements follow the graphical layout of the Fractree on the background.

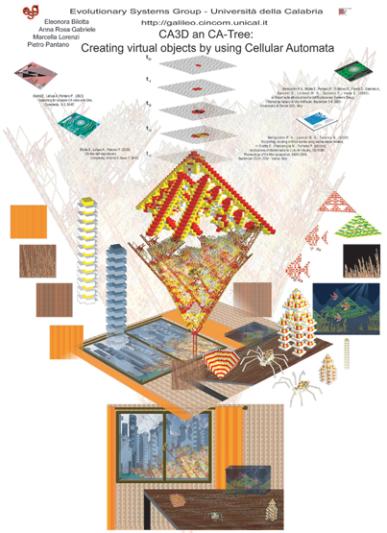
Figure 9: Poster

Figure 10: Example of artistical composition

References

[1]von Neumann J. (1966). Theory of Self-Reproducing Automata, Burks A.W Ed. University of Illinois Press, Urbana.

[2]Wolfram S. (2002). A New Kind of Science, Wolfram Media, Inc.

[3]Bilotta E., Lafusa A., Pantano P., (2002). Is self-replication an embedded characteristic of artificial/living matter?, In: Artificial Life VIII: Standish, R.K., Bedau, M.A., Abbass, H.A., Eds.; The MIT Press: Cambridge, MA; pp. 38–48

[4]Bilotta E., Lafusa A., Pantano P.  (2003). Life-like self-reproducers, Complexity,  9-1, pp. 38-55

[5]Bilotta E., Lafusa A., Pantano P.,  (2003). Searching for complex CA rules with GAs, Complexity,  8-3,56-67.  

[6]B.B. Mandelbrot, (1987). Gli oggetti frattali: forma, caso e dimensione, Einaudi,Torino.

[7]Barnsley M.F. (1988) Fractals Everywhere, Academic Press, New York.

[8]Peitgen H.O., Jurgens H., Saupe D., (1992). Fractals for the classroom, Springer-Verlag, New York.

[9]Bertacchini P. A., Bilotta E., Pantano, P., Di Bianco E., Fiorelli D.,  Gabriele A., Gervasi S., Lorenzi M., Sposato F.,  Vena S. (2003) Report sulle attività artistiche dell'Evolutionary Systems Group. I° workshop Italiano di Vita Artificiale, Università della Calabria, Settembre 2003.

[10]E. Bilotta, M. Lorenzi, P. Pantano, A. Talarico (2004). Poster: Art inspired by cellular automata. NKS Conference, Boston April 22-25, 2004.

[11]P. A. Bertacchini, M. Lorenzi, A. Talarico (2004) Storytelling: creating artificial worlds using mathematical models. Bilotta E., Francaviglia M., Pantano P. (a cura di) Applicazioni della Matematica all’Industria Culturale, Atti del Minisimposio, Convegno SIMAI 2004, CD-ROM, Venezia, 23-24 settembre 2004.