Complexity and Fractal Dimension
in 26 Mesoamerican
Pyramids
Dr.
Gerardo Burkle-Elizondo, Ph-D
Universidad
Autónoma de Zacatecas. Unidad de Postgrado II.
Doctorado en Arte
y Humanidades. Ave. Preparatoria s/n.
Col. Hidráulica.
CP 98060, Zacatecas Zac. México.
E-mail: burklecaos@hotmail.com
Prof.
Nicoletta Sala, Ph-D
Accademia di
Architettura (Academy of Architecture) di Mendrisio.
Universitá della
Svizzera Italiana (University of Lugano).
Largo Bernasconi ,
6850 Mendrisio. Switzerland.
E-mail: nsala@arch.unisi.ch
Abstract
Mesoamerica
is a region that comprises Mexico and upper Central America and where developed
a civilisation after about 1400 BC. The
Mesoamerican civilisations constructed numerous administrative and ceremonial
centres and erected numerous monuments. These reflect astronomic knowledge and
expertise in numeration and calendars. Mesoamerican Pyramids are
symmetric stable architectural forms that had resisted successfully the course
of time. More often they were built as a four-sided form with stairs in one
side almost always, and generally supporting a temple at the top. Pyramids had
a religious function and were associated with some god, fertility or war cult.
They were related too with a sacred mountain like a way to make contact with
the under and upper world (Tlalocan and Tamoanchan), and in the Maya case at
Palenque and other places we can see a temple
dedicated to an ancestor raised over his tomb. Other pyramids like at
Chichen Itzá were dedicated to celebrate the coming and end of time periods.
The holy landscape is usually inside the jungle or natural environment like a
dynamic and harmonic unit. The aim of this paper to show the results of a complex and fractal analysis which has involved 26 Mesoamerican pyramids; 17
belongs to the Maya culture and 9 to the Aztec and Mixtec cultures. In
agreement to recent studies connected to determine the complexity in the arts
and architecture, the images of the different Mesoamerican pyramids were
scanned and analysed to calculate Box,
Information and Mass Dimension and the log-log plots graphs. Final results evidenced high levels of
complexity in Mesoamerican pyramids connected to their symbolism.
1. Introduction
The
Mesoamerican civilisations realised numerous administrative and ceremonial
centres and erected numerous monuments (for example, pyramids and tombs), that
reflected astronomic knowledge and expertise in numeration and calendars.
Mesoamerican Pyramids are
symmetric stable architectural forms that had resisted successfully the course
of time, as shown in figure 1. The symmetry is used in different architectural
styles and through the centuries [1, 2].

Figure 1
Mesoamerican Pyramids evidence symmetric architectural forms (Temples I, and II
of Tikal)
More often the pyramids were built
as a four-sided form with stairs in one side almost always, and generally
supporting a temple at the top. Pyramids had a religious function and were
associated with some god, fertility or war cult [2]. They were related with a
sacred mountain like a way to make contact with the under and upper world
(Tlalocan and Tamoanchan), and in the Maya case at Palenque and other places we
can see a temple dedicated to an
ancestor raised over his tomb. Other pyramids were dedicated to celebrate the
coming and end of time periods. For example the pyramids located at Chichen Itzá. The holy landscape is
usually inside the jungle or natural environment like a dynamic and harmonic
unit. The aim of this paper is to introduce a research that analyses the
complexity of the Mesoamerican Pyramids using the Fractal dimension. The paper
is organized as follow: in the section 2 we present the complexity and fractal
geometry and their applications in architecture. The section 3 describes our
research and the results. In section 4 there are the conclusion and the section
5 is dedicated to the references.
2. Complexity and Fractal
geometry in architecture
For
many centuries architecture has followed the Euclidean geometry and Euclidean
shapes and we are not surprise to observe that the buildings have Euclidean
aspects. On the other hand, some architectural styles are informed by Nature,
and much of Nature is manifestly fractal and complex. o perhaps we should not
be so surprised to find fractal architecture. As we shall see, fractals appear
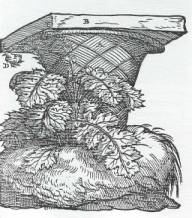
in architecture for reasons other than mimicking patterns in Nature. Figure 2a
shows a Vitruvius’s draw that describes the creation of the first Corinthian
capital. Figure 2b illustrates a Corinthian
capital.

 a) b)
a) b)
Figure 2 The creation of the Corinthian capital a) and a real Corinthian capital b)
The
Fractal analysis in architecture can be divided in two parts
[3]:
·
on a little scale
analysis (e. g, to analyse the single building shape);
·
on a large scale
analysis (e.g., to study the urban growth using a fractal point of view) [4,
5].
In the little scale analysis we can
observe:
·
the box-counting dimension (to determine the fractal
dimension of a design to use this parameter as a critical tool) [6, 7];
·
the building's self-similarity ( e.g., a building's component which repeats itself in
different scales) [3]
·
urban building generation using fractal algorithms
[8, 9].
Figures 3, 4 and 5 show three examples of self-similarity in the Chinese architecture, in Mesoamerican architecture, and in Hindu architecture respectively. Figures 6 and 7 illustrate two fractal organisation in African villages [10].The same shape is repeated in different scales.

Figure
3 The Hall of Prayer for Good Harvest (Temple of Heaven: “Tiantan”) Beijing
(China). It is an example of self-similarity in the Chinese architecture.
Tiantan, the Temple of Heaven, was established in 1420 during the reign of Ming
Emperor Yongle (1403-1424).
Fractals are self-similar because every smaller piece
of the objet, resemble the larger pieces and the whole depends on the
resolution used to make the measurement, and this produces a scaling
relationship that depends of a power law. This property means that the
Dimension is a measure of scaling and self-similarity. The Fractal Dimension Fd shows the way many additional smaller
pieces of an object are revealed when it is magnified and analysed in another
and fine resolution. This object fills up space, and it give us information
about area, length, form and volume. A data series and a time series can also
be fractal when it has self-similarity because describes how small changes in
the values measured in short time or amount values, are related to large
variations over long time.

Figure 4 Self-similarity in Mesoamerican
architecture (El Castillo, Chichen Itzá)


Figure 5 Self-similarity in Hindu architecture
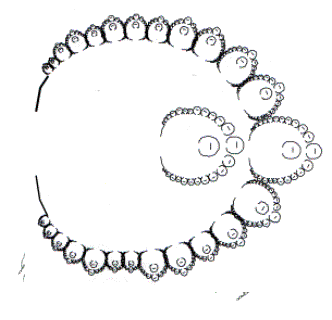
Figure
6 Fractal organisation in African village (Ba-ila, Zambia) [10, p. 27]
Figure
7 Fractal organisation in African village (Mokoulek, Cameroon) [10, p. 30]
3. Complexity in Mesoamerican
Pyramids: Our approach
The aim of our work is to
study the Mesoamerican pyramids’ structures trying to find out the patterns and
designs and the forms into this complex geometry that appear to enclose a
specific guide of information encode in them [7, 11, 12]. What we want attempt
is to decipher the possible interconnected nature of different reckoning systems.
To realize our research project we have
established three different procedures of analysis. The first one studies the
structures like series from the point of view of areas against volumes. In the
second procedure we visualize the pyramid like the reason of the volume
interpolated with its empty complement mould. The third one is the calculation
of the fractal dimension of a big number of pyramids using the Box counting
method that shows rather the roughness of an object or fluctuations of the
height over length scale. In the past we found out those Mesoamerican artworks,
sculptures and architecture have fractal dimension
The present study has special
interest to analyse the
interrelationships that in the past existed in Mesoamerica between the art, the
architecture of the cities, the religion, the nature, the society, the cosmos
vision and the empire, all these related to a ceremonial center. The problem in
the history and the proofs we have belongs to these three categories:
1. geographic-ecological,
2. sociopolitical,
3. symbolic.
In the last one we have to
consider the idea of a “sacred space”, integrated by the architecture, the
nature, the social order that includes the ritual practice and the symbols
included in the ceremonial complex that contains the buildings, the artistic
manifestations and the ritual it self.
We have to consider that the
cities plays a major role in the organization of the society and the government
to have the control at the same time in a sacred way. These ceremonial
capitals, some times monumental, were utilized like political technical to get
authority articulating the myth, the military policy, and the economic order
using an space erected on a grandiose scale, an image of the cosmos, of a time able to give motion to the empire and the
power and structure to the activities in an organising principle based in the
art, the architecture and symbolic details.
In
our approach we selected 26 Mesoamerican pyramids, we digitised their high
resolution images and using the program BenoitTM we calculated: the Box (Db), the Information
(Di), and the Mass Dimensions (DM). Figure 8 shows an example of
Log-log plot for “Tikal I” pyramid
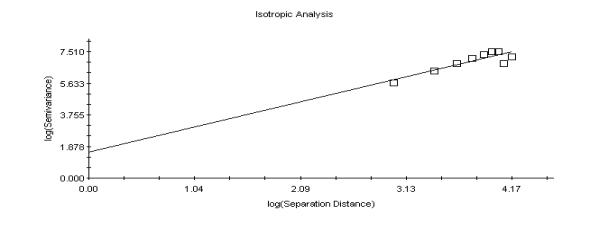
Figure
8 Log-log plot for "Tikal I" studied with Model Volume-Empty
Complement. (Fractal Dimension 1.28). The fractality can be appreciated as a
straight line.
In the table 1 we can observe the results of the Fractal
Dimension values that we obtained in each of the three procedures.
Table 1
|
PROCEDURES
AND METHODS TO STUDY THE FRACTAL
DIMENSION OF MESOAMERICAN PYRAMIDS |
|||||||
|
|
FRACTAL DIMENSION
METHOD Df (BENOIT) |
DIMENSION Dv FROM PROCEDURES 1 and 2 |
|||||
|
PYRAMIDS |
BOX
DIMENSION (Db) |
INFORMATION
DIMENSION (Di) |
MASS DIMENSION (Dm) |
VOLUME - EMPTY COMPLEMENT (Dv) |
S AREAS - S VOLUMES (Dv) |
SEG - MENTS |
|
|
Templo V Tikal |
1.940 |
1.937 |
1.9540 |
1.223 |
1.4950 |
14 |
|
|
± 0.016 |
± 0.003 |
± 0.086 |
± 0.206 |
± 0.339 |
|||
|
r2 =
0.835 |
r2 = 0.735 |
||||||
|
Templo I
Tikal |
1.925 |
1.951 |
1.995 |
1.286 |
1.204 |
12 |
|
|
± 0.019 |
± 0.0009 |
± 0.173 |
± 0.264 |
± 0.037 |
|||
|
r2 =
0.772 |
r2 = 0.993 |
||||||
|
Templo III
Tikal |
1.928 |
1.924 |
2.016 |
1.341 |
1.113 |
12 |
|
|
± 0.014 |
± 0.002 |
± 0.020 |
± 0.176 |
± 0.028 |
|||
|
r2 =
0.879 |
r2 = 0.996 |
||||||
|
Piramide
Uaxactun E-VII |
1.941 |
1.950 |
1.938 |
1.171 |
1.193 |
8 |
|
|
± 0.005 |
± 0.001 |
± 0.013 |
± 0.122 |
± 0.069 |
|||
|
r2 =
0.929 |
r2 = 0.977 |
||||||
|
Templo de
las Inscripciones Palenque |
1.922 |
1.938 |
1.936 |
1.117 |
1.157 |
12 |
|
|
± 0.011 |
± 0.001 |
± 0.011 |
± 0.079 |
± 0.038 |
|||
|
r2 = 0.966 |
r2 = 0.992 |
||||||
|
Templo del
Sol Palenque |
1.933 |
1.936 |
1.925 |
1.181 |
1.310 |
14 |
|
|
± 0.007 |
± 0.002 |
± 0.180 |
± 0.114 |
± 0.078 |
|||
|
r2 =
0.938 |
r2 = 0.976 |
||||||
|
Templo Mayor
de Cempoala |
1.932 |
1.947 |
1.917 |
1.221 |
1.100 |
20 |
|
|
± 0.005 |
± 0.002 |
± 0.043 |
± 0.113 |
± 0.029 |
|||
|
r2 = 0.936 |
r2 = 0.994 |
||||||
|
Xpujil
(Torre Lateral Sola) |
1.933 |
1.939 |
1.948 |
1.238 |
1.113 |
13 |
|
|
± 0.013 |
± 0.005 |
± 0.007 |
± 0.118 |
± 0.026 |
|||
|
r2 =
0.940 |
r2 =
0.996 |
||||||
|
Yaxchilan Estructura 30 |
1.934 |
1.955 |
1.973 |
1.277 |
1.317 |
13 |
|
|
± 0.020 |
± 0.001 |
± 0.035 |
± 0.197 |
± 0.081 |
|||
|
r2 =
0.857 |
r2 = 0.974 |
||||||
|
Piramide
Monte Albán Edificio M |
1.934 |
1.934 |
1.932 |
1.146 |
1.266 |
10 |
|
|
± 0.010 |
± 0.001 |
± 0.015 |
± 0.106 |
± 0.099 |
|||
|
r2 =
0.944 |
r2 = 0.959 |
||||||
|
Piramide de
Edzná Campeche |
1.938 |
1.955 |
1.960 |
|
1.101 |
6 |
|
|
± 0.010 |
± 0.001 |
± 0.066 |
|
± 0.030 |
|||
|
|
r2 = 0.997 |
||||||
|
Piramide 364
Nichos Tajin |
1.926 |
1.910 |
1.927 |
1.100 |
|
8 |
|
|
± 0.007 |
± 0.002 |
± 0.003 |
± 0.166 |
|
|||
|
r2 = 0.879 |
|
||||||
|
Piramide
Calixtlahuaca Adoratorio Ehecatl |
1.924 |
1.945 |
1.948 |
1.224 |
|
8 |
|
|
± 0.008 |
± 0.002 |
± 0.025 |
± 0.166 |
|
|||
|
r2 = 0.872 |
|
||||||
|
Piramide de
Cholula |
1.941 |
1.964 |
2.001 |
1.172 |
|
9 |
|
|
± 0.003 |
± 0.001 |
± 0.053 |
± 0.167 |
|
|||
|
r2 = 0.875 |
|
||||||
|
Templo IV
Tikal |
1.940 |
1.957 |
1.944 |
1.212 |
1.100 |
12 |
|
|
± 0.011 |
± 0.0008 |
± 0.013 |
±179 |
± 0.013 |
|||
|
r2 =
0.868 |
r2 =
0.999 |
||||||
|
|
FRACTAL DIMENSION
METHOD Df (BENOIT) |
DIMENSION Dv FROM
PROCEDURES 1 and 2 |
|||||
|
PYRAMIDS |
BOX
DIMENSION (Db) |
INFORMATION
DIMENSION (Di) |
MASS DIMENSION (Dm) |
VOLUME - EMPTY COMPLEMENT (Dv) |
S AREAS - S VOLUMES (Dv) |
SEG - MENTS |
|
|
Castillo Kukulcan Chichen Itza |
1.920 |
1.904 |
1.909 |
1.210 |
1.190 |
10 |
|
|
± 0.009 |
± 0.003 |
± 0.038 |
± 0.173 |
± 0.075 |
|||
|
r2 =
0.875 |
r2 = 0.973 |
||||||
|
Templo I
Tancah |
1.935 |
1.958 |
1.945 |
|
1.131 |
14 |
|
|
± 0.022 |
± 0.0009 |
± 0.006 |
|
± 0.031 |
|||
|
|
r2 = 0.994 |
||||||
|
Torre Gran
Palacio Palenque |
1.935 |
1.945 |
1.948 |
|
1.639 |
9 |
|
|
± 0.012 |
± 0.002 |
± 0.007 |
|
± 0.373 |
|||
|
|
r2 = 0.506 |
||||||
|
Templo de
Tlahuizcanpantecuhtli en Tula |
1.942 |
1.941 |
1.937 |
1.488 |
1.346 |
11 |
|
|
± 0.006 |
± 0.002 |
± 0.005 |
± 0.294 |
± 0.388 |
|||
|
r2 = 785 |
r2 = 0.632 |
||||||
|
Piramide de
Quetzalcoatl Teotihuacan |
1.937 |
1.946 |
1.952 |
|
|
|
|
|
± 0.006 |
± 0.002 |
± 0.010 |
|
|
|||
|
|
|
||||||
|
Observatorio
Chichen Itza |
1.927 |
1.943 |
1.894 |
|
|
|
|
|
± 0.009 |
± 0.003 |
± 0.010 |
|
|
|||
|
|
|
||||||
|
Templo del
Sol Teotihuacan |
1.923 |
1.913 |
2.000 |
|
|
|
|
|
± 0.004 |
± 0.003 |
± 0.014 |
|
|
|||
|
|
|
||||||
|
Templo del
Adivinio Uxmal |
1.908 |
1.911 |
2.085 |
|
|
|
|
|
± 0.006 |
± 0.0005 |
± 0.124 |
|
|
|||
|
|
|
||||||
|
Piramide del
Dios Descendente Tulum |
1.929 |
1.950 |
2.085 |
|
|
|
|
|
± 0.006 |
± 0.0005 |
± 0.126 |
|
|
|||
|
|
|
||||||
|
Piramide
Huichapa Edificio C |
1.937 |
1.967 |
1.952 |
1.158 |
|
12 |
|
|
± 0.020 |
± 0.001 |
± 0.006 |
± 0.107 |
|
|||
|
r2 = 0.944 |
|
||||||
|
Edificio de
las Columnas Mitla |
1.928 |
1.949 |
1.902 |
1.236 |
|
21 |
|
|
± 0.004 |
± 0.001 |
± 0.004 |
± 0.116 |
|
|||
|
r2 =
0.942 |
|
||||||
|
Las Chimeneas
Cempoala |
|
|
|
1.349
± 0.268 |
|
10 |
|
|
r2 = 0.760 |
|
||||||
GENERAL
1.312 ± 0.179 1.236 ±
0.108
AVERAGE 1.931 ± 0.010 1.941 ± 0.0017 1.959 ± 0.042 r2 = 0.874 r2 = 0.918 11.72
4. Conclusions
We
studied the Complexity and we analysed the Fractal Geometry in 26 Mesoamerican
pyramids; in 22 we found Fractal Dimension and Fractality with our models and
procedures using the s/w BenoitTM and the GS+ Programs; in other 4
pyramids we found only Fractal Dimension with the s/w BenoitTM. Most
of the buildings could be fractal objects.
Our data analyses on the fractality
and the complexity in Mesoamerican architecture could suggest us that the
architects of these pyramids tried to imagine some models observing the nature.
Basic symbolism representing their
cosmos vision are present in the Mesoamerican pyramids related with earth,
water and fertility, mountains and caves. All these symbols are the manifestations of a cult system that
included not only the cosmology, but the complex mathematics involved in it and
in the mythic and the ritual concepts. Mesoamerican architects conceived
spatial representations before building a pyramid or other of their monumental
works [11]. In our approach we found out some fractal models with
self-similarity properties, but it
would be speculative to conclude that comparison between our research and the
existing pyramids prove that the builders of these pyramids conceived their
models using the same structures that we have presented in this work [11].
The complexity of
Mesoamerican pyramids and their mathematics connections helped us to suppose
the existence of a symbolic model of
the universe, that evidences the mythic structures and the scientific
development reached, in ancient times, by the Mesoamerican cultures. We presume
that this mathematical computation,
which worked well for these
buildings, reflects the presence of
significant numbers and their fractal expressions out of a pure randomness. Our
findings lead us to believe in the possibility that, when the architects
designed their buildings, they were thinking on the basis of the concept of
movement. We can also suppose that Mesoamerican architects imagined and
designed their cities and temples with connections to the astronomical data and
to the patterns into these massive models [7, 11].
5. References
[1]
Stierlin H. (2001), The Maya
Palaces and pyramids of the rainforest, Taschen, Köln.
[2] Sala
N. and Cappellato G. (2003), Viaggio matematico nell’arte e
nell’architettura, Franco Angeli, Milano.
[3] Sala
N. (2002), The presence of the Self- Similarity in Architecture: Some examples,
Novak M. M. (ed.), Emergent Nature,
World Scientific, pp. 273 – 283.
[4] Batty
M. (1991), Cities as Fractals:
Simulating Growth and Form. In Crilly A. J., Earnshaw R. A. and Jones H. Fractals
and Chaos, Springer - Verlag, New
York, pp. 43 – 69.
[5] Frankhauser P. (1994),
La Fractalité des Structures Urbaines,
Collection Villes, Anthropos, Paris, France.
[6] Bovill C. (1995), Fractal Geometry in Architecture and Design,
Birkhäuser, Boston.
[7]
Burkle-Elizondo G., Fuentes-Larios A.G. and Valdez-Cepeda R.D. (2004),
Fractality and Fractal Dimension in Mesoamerican Pyramid Analysis, Novak M.M.
(ed.), Thinking in Pattern: Fractals and
Related Phenomena in Nature, World Scientific, Singapore.
[8] Saleri Lunazzi R. (2004), Pseudo-urban automatic pattern generation, Chaos and Complexity Letters, 3, pp. 127-138 (in print).
[9] Marsault X. (2004), Generation of textures and geometric pseudo-urban models with the aid of IFS, Chaos and Complexity Letters, 3, pp. 109-126 (in print).
[10] Eglash R. (1999), African Fractals: Modern Computing and Indigenous Design, Rutgers University Press, Piscataway.
[11] Burkle-Elizondo G., Sala N. and Valdez-Cepeda R.D. (2004), Geometric and Complex Analyses of Maya Architecture: Some Examples, Williams K. (ed.), Nexus V Architecture and Mathematics, Kim Williams Book, Fucecchio, pp. 57-68.
[12] Sala N. and Cappellato G. (2004), Architetture della
complessitŕ: la geometria frattale tra arte, architettura e territorio, Franco
Angeli, Milano.