Biomimesis and the Geometric Definition of Shell
Structures in Architecture
Semra Arslan Selcuk, PhD Candidate
Department of Architecture, Middle East Technical
University, Ankara, Turkey.
e-mail: semra@arch.metu.edu.tr
Al J Fisher, MEng
Department of Architecture and Civil
Engineering, University of Bath, UK.
e-mail: a.j.fisher@bath.ac.uk
Chris JK Williams, MA, PhD, MIStructE
Department of Architecture and Civil
Engineering, University of Bath, UK.
e-mail: c.j.k.williams@bath.ac.uk
Abstract
In architecture
the concept of biomimesis (bios,
meaning life, mimesis,
meaning to imitate, also known as biomimetics) can be applied to the design of tree-like,
web-like, skeleton-like, pneumatic and shell-like structures.
Shell structures may be constructed from masonry, concrete or a grid of steel or timber members – a lattice or reticulated shell. The paper examines the philosophical, æsthetic, structural and environmental criteria to be used to decide whether biomimesis is appropriate. A strategy is described for the generation of organic forms in which a three-dimensional computer model is produced using a combination of interactive sculpting and analytical relationships. The inspiration behind this approach is the geometry of seashells.
1. Introduction
A shell is a three dimensional curved structure which resists load through its inherent curvature. There are numerous shell structures in nature; eggs, skulls, nuts, turtles and seashells, are notable examples [1]. A shell’s structural behaviour is derived directly from its form, thus when designing a shell-like structure, the fundamental consideration is the choice of geometry. This not only dictates the æsthetics, but the overall efficiency and behaviour under load of the structural system. The basis for curved geometry, as discussed by Williams [2], can be sculptural, geometric or defined by a natural physical process.
There
are many precedents of the use of natural forms and phenomena as the basis for
architectural geometry. Techniques for forming optimum shapes for pure tensile
or compressive structures have been developed using physical models. Antonio
Gaudí aspired to create optimal structural forms using inverted string models,
taking his inspiration from Gothic architecture in Spain.
A string,
when suspended at each end and allowed to hang freely, forms a catenary, a
curve of pure tension. Using this principle Gaudí formed pure compression
geometries by inverting the form of the hanging models. Gaudí also experimented with
suspending cloth, allowing it to sag to create three-dimensional vault
surfaces. Throughout the twentieth century architects and engineers, including Torroja, Nervi, Candella and Isler, explored the design of thin concrete shell structures.
Figure 1 shows a service station in Deitingen-Süd, Switzerland, designed by Heinz
Isler. Much of Isler’s free-form geometry was generated using inverted hanging
models similar to Gaudí’s. Isler also went on to experiment with
pneumatic membrane models, creating what he called ‘bubble shells’, where the
geometry was defined by air inflated membranes [4].
In 1964
Frei Otto founded the Institute of Lightweight Structures at the University of
Stuttgart. Here Otto and his team undertook extensive research into natural
forms and processes, generating and inspiring optimum structures [5]. As well
as shell structures, lightweight or optimum structures include membrane
structures, cable-net, geodesic domes, inflatable and air supported structures,
and lattice or reticulated shell structures such as the grid shell pictured in
figure 2. As well as building on the historical precedents of inverted hanging
models for rigid compression structures, Otto pioneered the use of soap film
models to generate minimal surfaces defining the optimum geometry of tensile structures
(figure 3).
Further
examples of biomimesis in architecture may include Calatrava’s bone like structures [6], Meinhard von Gerkan’s tree-like roof of the Stuttgart Airport passenger
terminal or perhaps Nicholas Grimshaw’s geodesic domes of the Eden project in
Cornwall, which bear a striking resemblance to the hexagonal lattice of a
diatom, pictured in figure 3.

Figure
1: Concrete shell structure designed by Heinz Isler [3]

Figure
2: Grid shell roof covering the Great Court of the British Museum in London
Architect:
Foster and Partners, Engineer: Buro Happold
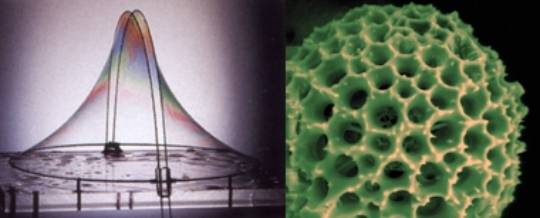
Figure
3: (left) Soap film experiment producing minimal surface [5]
(right)
Diatom, analogous to a geodesic dome [7]
Although there are numerous examples of where biomimesis has been successfully applied to architecture, the potential is far from being exhausted. There are endless different structural forms played out in nature, however in most cases the complexity of these forms renders geometric modelling problematic. Yet as computer-aided design and computational analysis techniques are becoming more powerful, greater interest is focused on these forms and even complex structural behaviour is modelled successfully. It is the aim of this paper to describe a method for modelling seashell forms with an application in architectural design.
As described above a shell’s inherent shape
defines how efficiently loads are resisted. Loads applied to a shell surface
can be accommodated through two actions, through bending and through stretching
[8]. Bending forces are carried through moments and shear forces, and
stretching forces through axial thrusts and tensions. The later of these
phenomena is called membrane action. Membrane action is much more efficient than bending, and therefore a shell
will work by membrane action if it can, however to determine whether a shell
can or not depends greatly upon its geometry and support conditions. Membrane
action also relies on bending stiffness to prevent buckling. Therefore in order
to understand the structural behaviour of seashells a complete understanding of
their geometry is required.
2. Geometry of Seashells
Seashells are formed in nature by growth at the shell’s free leading edge. Their increase in overall size is achieved purely from successive addition of material to one end only [9]. From inspection of actual seashell cross-sections, the older previously formed parts of the shell remain, on the whole, unaffected and geometrically unchanged once produced (as illustrated in figure 4).

Figure 4: Cut cross-sections of a selection of seashells found in nature
A simple seashell may be considered as a surface of revolution formed along a spiral path about the shell’s axis. The generating cross-section is of constant shape, but increasing in size by a constant ratio as the section sweeps the curve. For centuries biologists and mathematicians have explored techniques for describing and dissecting this shell geometry into simple terms.
The origins of theoretical seashell morphology can be traced back to the work of Moseley, who derived equations for calculating the volume, surface area, and centre of gravity of planispiral and trochospiral shells [10]. Moseley's equations were reformulated by Raup with the application of displaying shell shapes using a computer [11]. Raup described the geometry of seashells using three parameters, which he called W, D and T. These terms were later elaborated by Dawkins [12], renaming them flare, verm and spire, respectively.
Flare, Dawkins explains, is a measure of the expansion rate of the spiral, verm controls the rate of increase in size of the cross-section and spire is the rate of displacement along the axis of the shell. Figure 5 illustrates the effect on the overall shell geometry for changes in these different parameters, using an ellipse as the whorl cross-section. However it is clear from observations of actual shells (figure 4) that the cross-section is more complex than the input of three parameters allows. Fowler et al. [13] were first to implement free-form cross sections, using a Bézier curve [14,15] as the input.
All these approaches model the shell as a single surface, a two-dimensional object, embedded in three-dimensional space. To the writers’ knowledge little work has been done on accurately modelling the cross-section of the shell, showing the thickness of the shell wall and the complex solid volumes that are formed down the internal spine. As described above shells as a structural mechanism are incredibly sensitive to variations in geometry. It is this paper’s intent to create a method for generating a three-dimensional shell model which includes the thickness of the shell material, thus providing a model which can form the basis of a three-dimensional structural analysis.
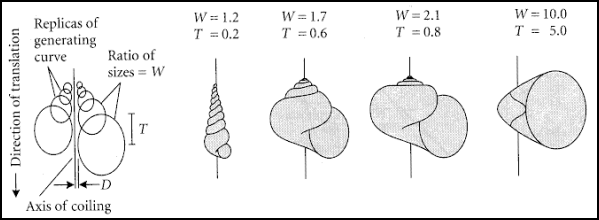
Figure
5: Shell geometry controlled by parameters flare (W), verm (D) and spire (T) [11]
3. Construction of the shell model
The
basic approach to modelling the shell’s solid cross-sections was to first
generate the internal whorl surface which forms the cavity in which the
gastropod lives. A portion of this surface could then be offset defining the
outermost surface of the shell. The volume between these two surfaces would
then form the geometry of the solid material which forms the shell.
A
parametric model of the shell was set up using the cross section of a single
whorl as the input. In a similar approach to Fowler et al [13], the shape of a single typical whorl was defined as a
B-spline. A B-spline can be used to approximate a smooth curve from a small set
of control points [14,15]. Figure 6 shows a B-spline of order four, and its
control polygon.
From the
definition of a B-spline the curve is parameterised along its length, with
respect to parameter m with a range of 0 £ m £ 1.0. m = 0 and 1.0 refer to the start and end of
the closed loop respectively whilst the point m = 0.5 is half way around the length of the
curve.
Between the values mbegin = 0 and mjoin the whorl B-spline is offset by a given thickness to form the outer surface of the shell. The outer surface is parameterised between fbegin and fend. A single whorl cross-section in its local coordinate system is illustrated in figure 6.
The ribs on the external shell surface, as illustrated later in figures 9 and 10, were generated by superimposing a sine based function on to the surface normal component of the position vectors.
The
shell surface geometry is defined using cylindrical polar coordinates (r, q, z), which can be expressed in
terms of Cartesian coordinates (x, y, z):
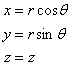 (1)
(1)
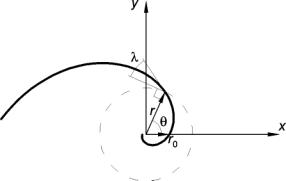
The path along which a shells whorl cross-section follows is a logarithmic spiral and it is the geometric properties of this curve that define the overall geometry of the shell. A logarithmic spiral is a curve which forms a constant angle between its tangent and radius vector at any point. Hence logarithmic spirals have the alternative name equiangular spirals. Figure 7 illustrates the constant l which defines the rate of spiral for any such curve.
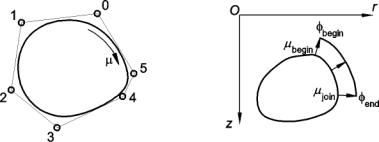
Figure
6: (left) B-spline and its control polygon
(right) single whorl cross-section
Figure
7: Geometry of the logarithmic spiral.
The relationship between any two points on a logarithmic spiral can be described by the formula below:
![]() (2)
(2)
giving
![]() (3)
(3)
where r0 is the radius at q = 0.
From
observations made from real seashells the growth rings, which correspond to the
whorl cross-section, are not radial and do not even lie in one plane. They are
curves in three dimensions. This means that the shell’s rate of spiral, l, as previously illustrated, is required to
be such that the point fbegin on the current leading edge
cross-section must lie coincident with fend on the preceding section after slightly less
than one revolution about the major z-axis, i.e. Dq = 2p - qjoin,
as illustrated in figure 8 and expressed in the following equation (4):
![]() (4)
(4)
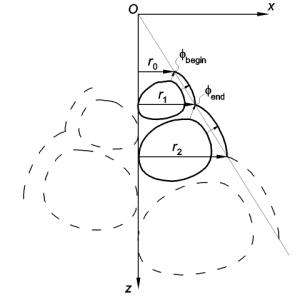
Figure 8: Geometric relations of the shell surface
Thus l is controlled by the relationship:
![]() (5)
(5)
where:

The
growth constant is applied to the whorl by transforming its coordinates using
the formulae below, based on the cylindrical polar coordinate transformation
(equation (1)):
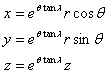 (6)
(6)
Figure 8
illustrates the sequential increase in size of the cross-section, starting from
an infinitesimal size at the origin.
The shape of the whorl, the value of fend and the offset thickness are all parameters easily measured from actual seashell cross-sections and it is from these inputs that the whole three-dimensional shell geometry can be generated. Figure 9 illustrates a good correlation between the real natural seashell on the left and the computer generated model on the right.

Figure
9: (left) scan of a seashell found in nature
(right) computer generated shell model
4. Conclusions
Seashells were investigated as three-dimensional structures as part of a study into biomimesis as a basis for architectural form. Previous seashell models have accurately captured the external surface of the shells, generating realistic images; however our research has placed emphasis on the shell as a volume. Figure 10 shows a three-dimensional model which has been clipped to reveal the central third of the shell, illustrating the incredibly complex volumes and voids which are generated internally. The next phase of the research is to understand the structural implications of this geometry and thus suggest a set of inspired architectural forms.
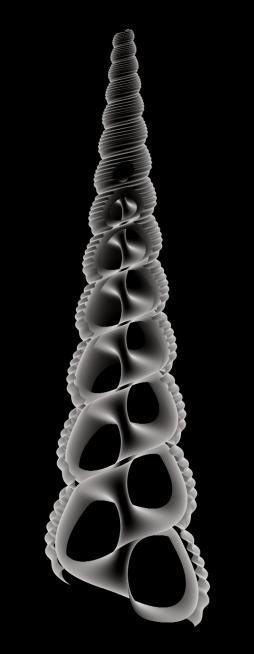
Figure
10: Three-dimensional shell model with two cutting planes at third points
References
[1] Arslan, S. and Gonenc Sorguc, A., 2004, Similarities in Structures in Nature and Man-Made Structures: Biomimesis in Architecture. Proceedings of the 2nd Design and Nature Conference Comparing Design in Nature with Science and Engineering, Rhodes, Greece, June 28th - 30th , 2004.
[2] Williams, C.J.K., 2000, The definition of curved geometry for widespan enclosures, Proceedings of the International Symposium on widespan enclosures, University of Bath, UK, 26th – 28th April 2000.
[3] Heinz Isler [Online] Available http://www.anc-d.fukui-u.ac.jp/~ishikawa/Aloss/data/Isler/ Catalog/Isler_catalog_files/main_catalog.html (Accessed 3rd November 2005)
[4] Lewis, W., 2005, Understanding novel structures through form-finding. Proceedings of the Institution of Civil Engineers, 158(4), pp. 178-185.
[5] Otto, F., 1995, Frei Otto, Bodo Rasch: Finding Form. Towards an Architecture of the Minimal . Deutscher Werkbund Bayern.
[6] Zardini, M., 1996, Santiago Calatrava Secret Sketchbook. New York: Monacelli Press.
[7] Northwestern University Atomic and Nanoscale Characterization Experiment Centre [Online] Available at http://www.nuance.northwestern.edu/ (Accessed 3rd November 2005)
[8]
Calladine, C.R., 1983, Theory of shell
structures. Cambridge: University Press.
[9]
D'Arcy Thompson, 1992, On Growth and Form.
Cambridge: University Press.
[10]
Moseley, H., 1838, On the geometrical forms of turbinated and discoid shells. Philosophical Transactions of the Royal
Society of London, pp. 351-370.
[11] Raup, D.M., 1961, The Geometry of Coiling in Gastropods, Proceedings of the National Academy of Sciences of the United States of America, Vol. 47, pp. 602–609.
[12] Dawkins, R., 1997, Climbing Mount Improbable. W.W. Norton & Company.
[13] Fowler, D.R., Meinhardt, H, and Prusinkiewicz, P., 1992. Modeling Seashells. Computer graphics, 26(2), pp. 379-387.
[14] Farin, G., 2002, Curves and surfaces for CAGD: a pratical guide. 5th ed. San Franciso: Morgan Kaufmann Publishers.
[15] Rogers, D.F., 2001, An introduction to NURBS with historical perspective. Morgan Kaufmann Publishers.