Swarm modelling.
The use of Swarm Intelligence to generate
architectural form.
Pablo Miranda Carranza Dipl ArchMSc
CECA University of EastLondon
Holbrook rd Stratford
London E15 3EA
e-mail: merluza@altavista.com
Paul Coates AA Dipl
CECA University of EastLondon
Holbrook rd Stratford
London E15 3EA
e-mail: p.s.coates@uel.ac.uk
Abstract
The
reason for choosing swarms as a study case is the fascination of the simplicity
of its mechanics and its complexity as a phenomenon. It can be compared in that sense with other models such as
Cellular Automata, for example, with which shares some similarities (they are
parallel systems, they interact at a local level, etc).
This
paper describes the swarms understanding them as examples of sensori-motor
intelligence. It begins addressing some issues already patent when studying
simple turtles, and then it looks at two ways of interaction of the swarm and
their implications. It studies the interaction with an environment in relation
with learning processes and simple perceptions of forms, and then uses the
processes developed in this first cases to look at the possibilities of
interaction of the swarm with a human, and its similarities with other systems
such as Genetic Algorithms or social systems.
In
general the paper discusses the morphogenetic properties of swarm behaviour,
and presents an example of mapping trajectories in the space of forms onto 3d
flocking boids. This allows the construction of a kind of analogue to the
string writing genetic algorithms and Genetic programming that are more
familiar, and which have been reported by CECA [22,23,24,25,26]
Earlier
work with autonomous agents at CECA [27, 28] were concerned with the behaviour
of agents embedded in an environment, and interactions between perceptive
agents and their surrounding form. As elaborated below, the work covered in
this paper is a refinement and abstraction of those experiments.
This places the swarm back where perhaps it should have belonged, into the realms of abstract computation, where the emergent behaviours (the familiar flocking effect, and other observable morphologies) are used to control any number of alternative lower level morphological parameters, and to search the space of all possible variants in a directed and parallel way.
1. Simple agents and turtles. Sensori-motor intelligence and perception
W.
Grey Walter built in Bristol the first recorded turtles, Elmer and Elsie, just
after the second world war. These first turtles raised many questions and
opened new paths in the field of early Artificial Live. Walter gave them the
mock-biological name Machina speculatrix, because they illustrated particularly
the exploratory, speculative behaviour that he found characteristic of most
animals. As he wrote, ‘Crude though they
are, they give an eerie impression of purposefulness, independence and
spontaneity.‘ ‘In this way it neatly solves the dilemma of Buridan’s ass, which
the scholastic philosophers said would die of starvation between two barrels of
hay if it did not posses a transcendental free will.’ [1]
Inspired by Grey.W. Walter's turtles, Valentino
Braitenberg [2] uses thought experiments in which very intricate behaviours
emerge from the interaction of simple component parts, to explore psychological
ideas and the nature of intelligence. In a sense, Braitenberg
"constructs" intelligent behaviour, a process he calls
"synthetic psychology". A similar approach has been taken in the
development of this work, starting from very simple agents or turtles
interacting in the real world, and then developing the idea further with the
use of swarm systems in the computer. Invention and deduction, as in
Braitenberg’s case, have been preferred over analysis and observation.
To begin with, a simple turtle was built, based in the
reflex behaviour by which moths and other insects are attracted to light, known
as "positive phototropism". In this mechanism the two halves of the
motoric capacity of an insect are alternatively exited and inhibited, depending
on the side from which they perceive a strong source of light, having the
effect of steering the insect towards the light source.

automaton moving on an environment
The automaton consisted of two light sensors connected
each to threshold devices and these to two electric motors (one in each side of
the body). The device is thus made of two completely independent effectors
(sensory-motor units). The automaton exhibits different behaviours depending on
the configuration of its parts. Changing in particular the position of the
light sensors respect to the rest of the components, the machine wondered in
different ways through a rectangular white area: sometimes groping the edges,
another times covering the whole surface, other times stopping at the corners.
Although all operations involved in the 'computation' of this automaton were
elementary, the organisation of these operations allowed us to appreciate a
principle of considerable complexity such as the computation of abstracts.
Notions such as the ones of "edge", "corner" or "surface"
emerged when different configurations of the body of the automaton were set in
the same test environment.
Though Von Foerster [3] already defined this emergence
of perception through sensor-motor interaction in the framework of second order
cybernetics, the biggest development of this idea of perception-in-doing comes
perhaps from the description of perception in autopoietic theory. For Maturana
and Varela, cognition is contingent on embodiment, because this ability to
discriminate is a consequence of the organism's specific structure. They call
this concept Enaction, where '...knowledge
is the result of embodied action’ and 'cognition
depends upon the kinds of experience that come from having a body with various sensorimotor
capacities ... themselves embedded in a more encompassing biological,
psychological, and cultural context ' [4].
1.1 Structural coupling
The most interesting idea in Autopoietic theory
referring to perception is the already mentioned Structural coupling, which
leads to the concept of enactive perception. It is '...a historical process leading to the spatio-temporal coincidence
between the changes of state in the participants ’ [5]. Structural coupling describes ongoing mutual co-adaptation without
allusion to a transfer of some ephemeral force or information across the
boundaries of the engaged systems. There are two types of structural coupling:
1) A System coupling with its Environment.
2) A System Coupling with Another System.' If the two
plastic systems are organisms, the result of the ontogenic structural coupling
is a consensual domain.'
Inside this framework it is interesting to observe is
how different 'forms' are described by the structural coupling of the automaton
and an environment. There is not any explicit description of those formal
concepts in the system, instead they are actually distributed through it, in
the 'environment' and in the way the light sensors are fixed in relation to the
motors. We could say that the device describes different 'gestalts' (a gestalt
being some property -such as roundness- common to a set of sense data and
appreciated by organisms or artefacts) or universal forms. In the next
experiments swarms are implemented to define and find such concepts of shape.
These experiments resemble Selfridge and Neisser’s Pandemonium machine for
pattern recognition, in which ‘Each local verdict as to what was seen would be
voiced by "demons"(thus, pandemonium), and with enough pieces of
local evidence the pattern could be recognised' [6].
2. Swarms
The relative failure of the Artificial Intelligence
program and its approach to cognition has forced many computer scientists to
reconsider their fundamental paradigm. This paradigm shift has led to the idea
that sensori-motor intelligence is as important as reasoning and other
higher-level components of cognition. Swarm-based intelligence relies on the
anti-classical-AI idea that a group of agents may be able to perform tasks
without explicit representations of the environment and of the other agents and
that planning may be replaced by reactivity. (R.Kube and E.Bonabeau) [7]. The
self-organisation of patterns of flow in social insect swarms is an example of
how intelligent and efficient behaviour of the whole can be achieved even in
the absence of any particular intelligence. Indeed, such patterns can have
functionality even without the awareness of the individual entities themselves.
A study of the essential elements of swarm dynamics provides an understanding
of such behaviours, where the most important of them is possibly the capacity
for self-organisation.
The collective behavioural characteristics of a group
of organisms must, of course, be encoded in the behaviour of the individual
organisms. Complex adaptive behaviour is the result of interactions between
organisms as distinct from behaviour that is a direct result of the actions of
individual organisms.
2.1 First case of structural coupling: Systems
coupling with an environment
As explained in the introduction the first experiments
with swarms are an extension of the work done with the automaton, in the
descriptions of form through sensori-motor devices. There are some different
numbers of paradigms of collective intelligence. Perhaps the most simple in
principle and many times spectacular is the modelling of flocks, herds and
schools, that give rise to quite appealing spatial configurations. Based on
Craig Reynolds computer model of co-ordinated animal motion, Boids (1986)[8], a
swarm of sensing agents was created, each of them reacting to a geometrical
environment through a collision detection algorithm, and combining their
actions through flocking. In the flocking or schooling of fish ‘individual members of the school can profit
from the discoveries and previous experience of all other members of the school
during the search for food. This advantage can become decisive, outweighing the
disadvantages of competition for food items, whenever the resource is
unpredictably distributed in patches’ [9]
The flocking rules were taken straight from Reynolds,
and implemented in C and C++, inside AutoCAD 14 first, and using OpenGL later.
2.1.1 The flock algorithm.
Each agent has direct access to the whole scene's
geometric description, but reacts only to flock mates within a certain small
radius of itself. The basic flocking model consists of three simple steering
behaviours:
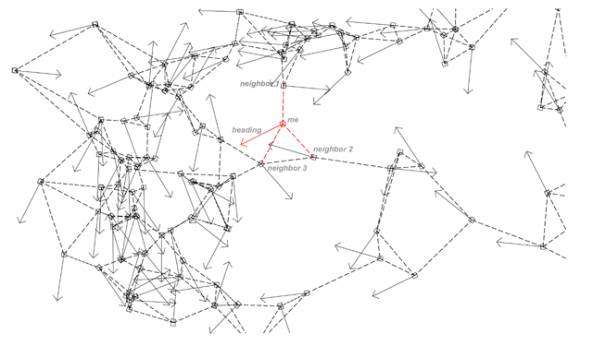
Diagram of the swarm. Arrows represent
each agent’s heading, dotted lines their closest neighbours.
Separation:
Gives an agent the ability to maintain a certain
separation distance from others nearby. This prevents agents from crowding to
closely together, allowing them to scan a wider area. To compute steering for
separation, first a search is made to find other individuals within the
specified neighbourhood. For each nearby agent, a repulsive force is computed
by subtracting the positions of our agent and the nearby ones and normalising
the resultant vector. These repulsive forces for each nearby character are summed
together to produce the overall steering force.
Cohesion:
Gives an agent the ability to cohere (approach and
form a group) with other nearby agents. Steering for cohesion can be computed
by finding all agents in the local neighbourhood and computing the
"average position" of the nearby agents. The steering force is then
applied in the direction of that "average position".
Alignment:
Gives an agent
the ability to align itself with other nearby characters. Steering for
alignment can be computed by finding all agents in the local neighbourhood and
averaging together the 'heading' vectors of the nearby agents. This steering
will tend to turn our agent so it is aligned with its neighbours.
Obstacle avoidance:
In addition, the behavioural model includes predictive
obstacle avoidance. Obstacle avoidance allows the agents to fly through
simulated environments while dodging static objects. The behaviour implemented
can deal with arbitrary shapes and allows the agents to navigate close to the
obstacle's surface. The agents test the space ahead of them with probe points.
When a probe point touches an obstacle, it is projected to the nearest point on
the surface of the obstacle and the normal to the surface at that point is
determined. Steering is determined by taking the component of this surface
normal, which is perpendicular to the agent's heading direction. Communication
between agent and obstacle is handled by a generic surface protocol: the agent
asks the obstacle if a given probe point is inside the surface and if so asks
for the nearest point on the surface and the normal at that point. As a result,
the steering behaviour needs no knowledge of the surface's shape.
Results:
In this first experiment, as a result of the way the
collision detection algorithm worked (slowly rectifying the heading of the
agent until it found a collision free trajectory), the individual agents had a
tendency to align with the surfaces of the geometric model of the site. This
ended in the emergence of the 'smoothest' trajectory on the environment, which
in the case of the test model of a site where the meanders of a river. The
swarm is able to discriminate the edges of a long wide curvy grove, that is,
the geometric form of the river, from any other information such as buildings or
building groups or infrastructures.

Traces
left by the agents.
2.1.2 Ants, networks and learning swarms.
The second experiment with swarms tried to incorporate
the capacity for learning that we find in many social insects. This is many
times achieved through their relation with the environment, through stigmergy
and sematectonic communication.
Grassé introduced stigmergy (from the Greek stigma:
sting, and ergon: work) to explain task co-ordination and regulation in the
context of nest reconstruction in termites of the genus Macrotermes[10]. Grassé
showed that the co-ordination and regulation of building activities do not
depend on the workers themselves but are mainly achieved by the nest structure:
a stimulating configuration triggers the response of a termite worker,
transforming the configuration into another configuration that may trigger in
turn another (possibly different) action performed by the same termite or any
other worker in the colony [11]. Individual behaviour modifies the environment,
which in turn modifies the behaviour of other individuals. The process is
called sematectonic communication [12], when the only relevant interactions
between individuals occur through modifications of the environment.
Systems such as these show self-organisation of higher
complexity than the initial flock model. Furthermore, it is possible to make a
connectionist interpretation of the mechanics of such a system, and realise
that it shows the same basic properties of a network [13]. Through this reading,
and comparing it with a network it is easy to appreciate the capacity of a
sematectonic system in terms of 'learning'.
In Connectionist models structure consists of a
discrete set of nodes (neurones), and a specified set of connections between
the nodes (synapses). The network unfolds as a dynamic process in which
different variables related to the transitions between nodes, or connection
strengths, are modified. The dynamics of the whole system is the result of the
interaction of all the neurones.
In its most general sense, learning can be described
in connectionist models as how the connection strengths, and hence the
dynamics, evolves. In general there is a separation of time scales between
dynamics and learning, where the dynamical processes are much faster than the
learning processes. In addition to neural networks there are many other types
of connectionist models, such as autocatalytic chemical reactions, classifier
systems, and immune networks, to mention just a few. Swarm networks are just another
example.
Incorporating these ideas in to the swarm,
sematectonic communication was implemented instead of flocking. For this, a
three dimensional lattice space was provided. Agents move in this discrete
space, each lattice being equivalent to a node in a connectionist system. Each
agent leaves a trace in the morphogen variable (from Millonas) on each lattice
(or node). The lattice space is also capable of computations on its
neighbourhood, similar to Cellular Automata. The computations of the nodes are:
Diffusion: local averaging of the morphogen values, in
order to generalise to neighbour nodes, and to generate smoother gradients for
the agents.
Evaporation of the morphogen: slow reduction of the
morphogen values, as explained earlier, to give the network the capacity of
'forgetting'. Necessary to discriminate the relevance of information, and
therefore to learn.
Gradient calculation: This is performed by the nodes
themselves instead of by the agents. It corresponds to the 'weights' in the
transition probabilities from one node to another (in the case of this lattice
space one of the neighbour nodes). Agents read the gradient and add it to their
current heading.
The way the gradients modify the possibility of an
agent moving from one node to another is understood as the changes in the
weights or the strengths of the connections between nodes, and therefore as the
learning of the system. The lattice space and the accumulation of morphogen in
it work as a memory and the slow "evaporation" of the morphogen as
the capacity to 'forget', and therefore to discern significant patterns from
irrelevant ones. After some time, areas with bigger concentrations of morphogen
differentiated from others.
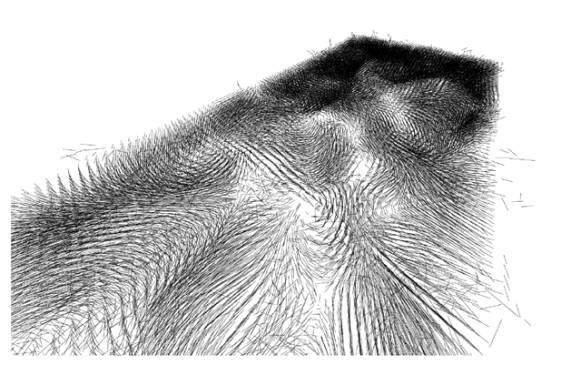
Gradients
created by the sematectonic process.
A next step was to differentiate and learn between
different "experiences" or sensed data by the agents. The agents
would therefore “secrete” more morphogen when they 'sensed' geometry, and less
when they had a clear view ahead of them. This ends up with the agents discerning
different parts of the geometrical model, and clustering in areas where their
collision detection algorithm informed them of higher spatial complexity (in
the terms of the agents). In other words, spaces where the agent's collision
detection algorithm found conflicts with the geometry (trying to steer away
from one collision path and entering in to another, for example) at the same
time spaces relatively easy to reach are rarely visited since otherwise the
morphogen would evaporate if not visited by any agent.
2.1.2 Adaptative flock
In their paper 'The use of Flocks to drive a
Geographic Analysis Machine', J. Macgill and S. Openshaw [14] discuss how the
emergent behaviour of interaction between flock members might be used to form
an effective search strategy for performing exploratory geographical analysis.
The method takes advantage of the parallel search mechanism a flock implies, by
which if a member of a flock finds an area of interest, the mechanics of the
flock will draw other members to scan that area in more detail.
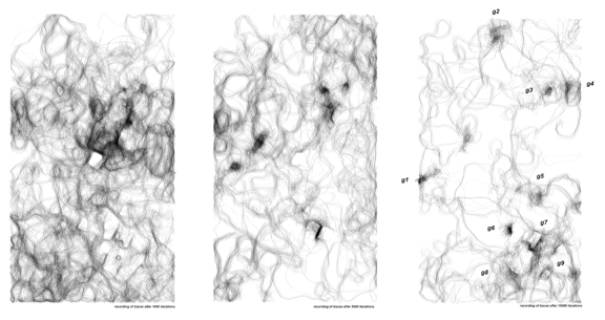 Result of the learning process in the site after 1000
, 5000 and 10000 iterations (8 hours).
Result of the learning process in the site after 1000
, 5000 and 10000 iterations (8 hours).
The third swarm therefore was again of a flocking
kind. One of the advantages of these is that since the lattice space and all
its Cellular Automata operations such as diffusion are not needed anymore, it
is possible to reduce enormously the amount of computation necessary.
The system shows the same characteristics for
cognition explained earlier, that is, the capacity for remembering and
forgetting, which we described when describing evaporation of the morphogen as
essential in the process of learning.
The Algorithm.
Each agent would have now a variable speed, with a
common minimum and maximum for all agents. In case of collision trajectory, the
agent will slow down. In the absence of collision, the agent will steadily
speed up until it reaches its maximum. This means that in the event of a
'conflict' space, or an area where one agent detects many collisions consecutively,
agents will cluster; since their speed is low, they will have the inertia to
remain there, where as faster 'free' agents in the neighbourhood will be easily
attracted to the area. The information about collision areas is therefore
stored in the speed of the agents. Speeding up will be the equivalent of
forgetting in the system.
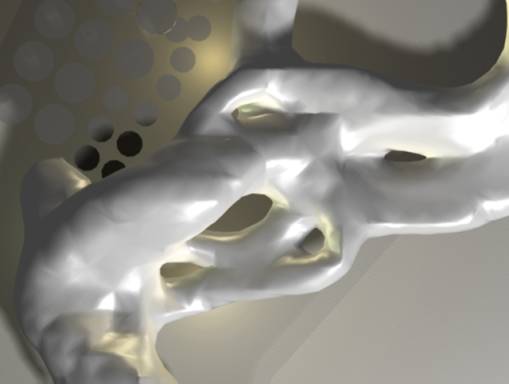
Isosurface wrapping the paths of the
agents.
With this mechanism, the swarm will move around detecting
collision areas. If the area doesn't have enough weight compared with another,
it won't be able to attract enough agents. The system will end up
discriminating the areas were most collisions occur and which are more
accessible, after a time.
2.2 System Coupling with Another System and consensual
domains
Until now, swarms have being moving in geometrical
representations of spaces. These swarms have been shown to have the ability to
define different qualities of their environment, comparing patterns of
collisions and unfolding a learning process.
The space agents move in doesn't necessarily need to
be any representation of physical space. It is possible to use the swarms of
the different types to perform searches in n-dimensional phase spaces. The
possibilities of this approach as an optimisation mechanism have been
underlined by Eberhart and Kennedy [15], and their performance compared with
similar search engines and devices such as Genetic Algorithms. One possible
advantage of this approach is the easy understanding of the relation between
the search mechanism and the solution space, and the way this search is
performed. It also makes it possible to compare the process with other evolving
systems, like the evolution of ideas, opinions and beliefs in social systems.
In
the next step such a device has been built and tested for its ability to
respond to human interaction. We have in this case the second type of
structural coupling described previously as the coupling of two systems, which
define a consensual domain. This can be described as the sphere defined by ‘ interlocked (intercalated and mutually
triggering) sequences of states, established and determined through ontogenic
interactions between structurally plastic state-determined systems.' [16]. We could also find this consensual
domain when looking at the relations between agents in the previous swarms. The
difference now is that this domain exists also between the swarm as a whole,
and a human partner.
2.2.1. The Algorithm
The algorithm for this swarm is also a development of
the basic Reynolds Boids algorithm, where each agent has been given a mass
variable in order to incorporate the capacity of learning as well. The acceleration the individual agents
experience each iteration depends on this variable: light weights mean higher
speeds, heavy weights slower ones. The cohesion of the flock is also influenced
by the mass: heavy agents will attract others to their neighbourhood stronger
than light ones. Light agents will also have less inertia, where heavy ones
will tend to keep their variables unmodified.
The system needs the slow “evaporation” of the mass
variable in order to be adaptative and therefore to learn.
Some “sympathetic mass transition” has also been
implemented, in order to make agents in the close neighbourhood of a very heavy
one become also heavier and slower, and consequently clustering in that region
(In the previous swarm this happened automatically from the interaction with
the environment).
The weight that is assigned to each agent could have
its origin in a “fitness function”. The position of each individual of the
swarm would then be mapped onto a “phenotype” and a fitness value calculated
for it. In cases of good fitness a heavy weight would be given to the individual,
to indicate the system that that position is worth keeping and mimicking. Bad
positions would this way be forgotten, since the agents in those areas would
have low inertia and the tendency to move rapidly away from them, towards more
successful territories. Regions with good values will compete with others for
the attention of the agents, and if not successful enough, they will be
forgotten.
The implementation of a strategy based in the
assignment of weight seemed appropriate in this particular case where there is
interaction with a human. In a more general case it would be possible to
evaluate each position for each iteration. In this case the difference of
position are very small for each iteration and therefore the communication with
the user and testing of the positions must be made at intervals of many
iterations. The mechanism for copying some of the weight of heavier neighbours
allows agents to react to the result of the “fitness” of those neighbours
without direct testing of each particular position for each iteration. Of
course this or a similar mechanism would also allow the testing of fitness at
separate intervals, and therefore it would improve the economy of calculations
of the algorithm.
In this instance of the flocking algorithm no specific
fitness function has been assigned, using instead a so-called “eyeball test”,
in which a human partner decides which position is more fitted. The process of
interaction between both defines what has previously been described as a
consensual domain.
Additionally
to Reynolds basic flocking algorithm, the agents choose sometimes one of their
neighbours randomly. This rule has been found to be an effective way of
avoiding the creation of completely uncommunicated and unrelated clusters of
neighbours, allowing the swarm to adapt faster.
The
collision avoidance with each other is also worth mentioning again in this
context. It introduces slight discrepancies between the positions of the
individual agents (they will have similar positions, but not the same one, or
in other words, the phenotypes will be very similar but most of the cases not
completely identical). This last element is in contrast with what Kennedy and
Eberhart explain in their paper, about the possibility of for example two
‘opinions’ sharing the same space [17]. The introduction of these differences
in position allows the agents to scan areas more thoroughly and extensively,
particularly helpful when working with design spaces and “eyeball test” kinds
of fitness.
The
way the space is mapped in to a phenotype is simple: in this case the
three-dimensional space defined has been understood as the parameters for a
branching algorithm. Each of the values of the position vector of the agents
becomes a rotation angle around X, Y and Z in the branching of the phenotype.
It is thus not necessary to have an infinite space, but it can be bounded
between 0 and 360 in each of the axes. The decision of using such an algorithm
as a phenotype is not arbitrary. First it allows to create a big variety of
different forms from very few parameters, which was reduced to three in this
case to allow the demonstration of the operations of the swarm (the
representation of spaces of higher dimensions has obvious difficulties).
Secondly, it produces forms with many symmetries, in which patterns can be
easily recognised and forms classified by the human partner. Therefore the
choice of such a phenotype is not aesthetic, but functional.
2.2.2. The program: Evolutionary Swarm.
Evolutionary Swarm is a Windows application developed
to test the capacity of a swarm algorithm to define a consensual domain. It
implements the algorithm previously described and provides it with an
interface. This interface is made of two basic windows: one in which the swarm is
shown in relation with the search space, and another one in which the position
of each individual has been mapped in to a phenotype, through a branching
algorithm. Each of these phenotypes can be selected by the user, increasing in
this way the mass variable of the agent associated with that position. The
agent will accordingly slow down and tend to remain in the vicinity of that
space. Because of the dynamics of the swarm, the position of the phenotype
selected will be ‘mimed’ by the rest of the individuals and reproduced with
more or less accuracy through out the agent population. For generating more
diversity among the swarm it is only necessary to evolve it without any
particular member selected. This will increase the differences between the
individual positions (less consensus) and therefore the variety of the
phenotypes.
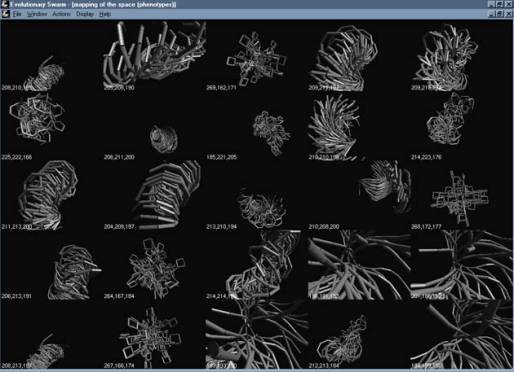
screensave of the interface of the
evolutionary swarm.
2.2.3 Parallels with social systems
Parallels between biological evolutionary systems and
the development of ideas have often been made, being perhaps the one implied in
the concept of memetic evolution the most popular of such comparisons. The word “meme” was coined by Richard
Dawkins in his book The Selfish Gene. Memes tend to make copies of themselves and
are therefore “replicators”, like genes.
` Examples of memes include melodies, icons, fashion statements and
phrases. Memes function the same way
genes and viruses do, propagating through communication networks and
face-to-face contact between people’ [18].
In this context the flock positions of its individuals
could also be compared with opinions, preferences etc, where the movement of
the individuals would be equivalent to the shift of those opinions inside a
social system. Individuals may hold some ideas or positions, and at the same
time show some 'sympathies' or tendencies towards others, often in the close
vicinity of the ideas that they currently hold. If these sympathies are
sustained for long enough or are very strong, the positions will shift towards
the sympathised convictions. This idea of sympathies or tendencies is similar
to the direction vectors in the swarm model. The different clusters of agents
that emerge and the region they define could be compared in a social system
with close sets of ideas, "ideologies" or shared beliefs.
Since
there is some kind of ‘conversational’
human/machine relationship between the swarm and a person interacting with it,
the forms work in some way as signs, in the sense that they are interpreted by
the person and meanings attached to them, such as good/bad, spider-like,
spongy, etc. The swarm tends to ‘understand’ and ‘agree’ with the choices made
by the person interacting with it, but it also seems to ‘disagree’ slightly, or
at least to not fully understand the preferences of the user. It is only in
this way that the conversation is possible, and the consensual domain formed.
If the machine would agree immediately, that is, if all agents would converge
exactly to the point specified, conversation would be impossible. Through this
game of differences the conversation can evolve.
Thus, if we understand the forms of the phenotypes as
some kind of sign their relations are similar as the signs in a linguistic
system. The mechanics of these resembles the one of the swarm: ‘As soon as a certain
meaning is generated for a sign, it reverberates through the system. Through
the various loops and pathways, this disturbance of the traces is reflected
back on the sign in question, shifting its ‘original’ meaning, even if only
imperceptibly. …Each trace is not only delayed, but also subjugated by every
other trace’. [19]
Even
more similarities emerge if we think of a phase space of signs, or the space of
all their possible meanings. ‘Words or
signs, do not have fixed positions. The relationships between signs are not
stable enough for each sign to be determined exactly. In a way interaction is
only possible if there is some ‘space’ between signs. There are always more
possibilities than can be actualized (Luhmann 1985). The meaning of a sign is
the result of the play in the space between signs. Signs in a complex system
always have an excess of meaning, with only some of the potential meaning
realized in specific situations.’ [20]
2.2.4 Comparison between models of adaptation.
As we have seen in comparison with a memetic system
the swarm model in relation with the evolution of ideas is more akin to their
emergence through smooth changes of opinion than with the actual spontaneous
birth of them. The discovery of new ‘ideas’ in the swarm is performed in a
smooth way, by the tendency of the agents to overpass an optimum point and by
the amplification of these mistakes. This slow evolution and drift between
ideas becomes one of the substantial differences between Genetic systems such
as the one constituted by memes, in which there is a random search mechanism
involved (mutation) and that of the swarms, in which the shifting towards new
‘ideas’ is smooth. If mutation in memetic systems is thought as the
accumulation of miss-replications or memetic drifts, the smoothness of the
evolution of the swarm could then be understood as an equivalent continuous and
low intensity memetic drift. In the swarm evolutionary paradigm random
mechanisms similar to mutation could also be implemented, as perhaps the
possibility of random jumps of the agents inside the search space.
But
there is also possible to highlight other differences between the genetic and
the swarm models. Carl Popper [21] distinguishes between two basic levels of
adaptation: genetic adaptation and behavioural adaptation. The main difference
between the genetic and the behavioural levels of adaptation is this: mutations
at the genetic level are not only aleatory, but also completely “blind”; they
are not directed towards an end, and the survival of a mutation can not
influence in the posterior mutations, not even in the frequency or in the
probabilities of their apparition. In the behavioural level trials are also
more or less random, but they are not completely “blind” in any of the ways
mentioned. In the first place they are directed towards an end, and in the
second, animals can also learn from the production of a trial. According to this, the swarm model could be
compared to some extent with the behavioural model of adaptation, in the sense
that the direction vectors of each individual can be interpreted as ‘directed
towards an end’ (in the abstract space to optimise their positions). The
direction vectors, at the same time also influence next ‘mutations’, or shifts
in position. Popper also emphasises how behavioural adaptation is in general an
intensively active process: in the animal –especially in the play of the young
animal –, and even in the case of the plant, which investigates actively and
constantly its environment.
Conclusion.
In
this paper we have discussed the development of sensori-motor intelligence and
its particular instance of the swarms. Those have been extensively studied from
this point of view, and different models of them tested. Processes of learning have
been developed through different approaches first in swarms that evolve in a
geometrical environment, and finally in an abstract representation of a design
space. The possibilities of such a model have been explained and then the model
has been compared with evolution of ideas in social sitemaps and with other
evolutionary systems, in particular genetic systems. Most of the conclusions
established about this last model of swarm could also be extended to others.
Instead of flocking algorithms, stigmergic swarms could be implemented in
similar ways.
References.
1.
Walter, W. Grey ‘An Imitation of Life’,
Scientific American, 182(5), pages 42-45,1950.
2. Braitenberg, Valentino ‘Vehicles: Experiments in Synthetic Psychology’, MIT Press, (Mass)
1984.
3.
Von Foerster, Heinz, On Constructing a Reality in ‘Observing
Systems’, Intersystems Publications, 1984.
Pages 288-309.
4. Maturana, Humberto ‘The organization of the living: A theory of the living organization’,
International Journal of
Man-Machine Studies,
Vol. 7 (1975). From Randal Whitaker,Tutorial Autopoiesis and Enaction, Umeå
Universitet (Sweden)
http://www.informatik.umu.se/~rwhit/Tutorial.html
5.
Ibid 4.
6.
Negroponte, Nicholas ‘The Architecture Machine’, MIT Press,
(Mass).
7.
C.
Kube, Ronald and Bonabeau, Eric ‘Cooperative transport by ants and robots’ (online
paper).
8. Reynolds, C.W. Flocks,
herds and schools: a distributed behavioural model. Computer Graphics, 21(4).
On line: http://hmt.com/cwr/boids.html
9. Wilson, E.O.
‘Sociobiology: the new synthesis.’ Cambridge
MA: Belknap Press, 1975.
10. Grasse, P. ‘La reconstruction
du nid et les coordinations interindividuelles chez Bellicositermes
natalensis et Cubitermes sp. La theorie de la stigmergie: essai d'interpretation
du Comportament des Termites Constructeurs’
Insectes Sociaux 6 (1959). Pages 41-48. 11.
in
Bonabeau, Eric , Dorigo, Marco and Theraulaz ,
Guy ‘Swarm Intelligence. From Natural to
Artificial Systems’ Oxford University Press, 1999.
12.
Ibid 9.
13. Millonas Mark M.’Swarms, Phase Transitions, and Collective
Intelligence’ in Artificial Live III Ed. Christopher G. Langton, SFI
Studies in the Sciences of Complexity, Proc Vol XVII, Addison-Wesley 1994.
14. MacGill, James and
Openshaw, Stan ‘The Use of Flocks to
drive a Geographic Analysis Machine’ (online paper) www.geog.leeds.ac.uk/pgradspj.mcgill/gis.html.
15. Eberhart, Russ and
Kennedy, James ‘Computational
Intelligence’ PC Tools, AP Professional, USA 1996. http://www.engr.iupui.edu/~shi/Coference/psopap4.hrml
16. Ibid 4.
17. Ibid 15.
18.
Dawkins,Richard . ‘The Selfish Gene’
Oxford, Oxford University Press, 1976.
19. Cilliers,Paul . ‘Complexity and Postmodernism. Understanding complex systems’ Routledge,
London, 1998.
20. Ibid 18.
21. Popper, Karl. ‘The
myth of the framework. In defence of science and rationality’ Routledge,
London, 1994.
22.
Coates P.S & Amy Tan ‘Using Genetic
programming to explore design worlds’ Middlesex Art & Design research
colloquium 1996
23. Coates
P.S. A.Tan & T Broughton ‘Using Genetic programming to explore design
worlds’ Caad Futures 97 Munich August
1997
24. Coates
P.S. H.Jackson ‘Evolving spatial configurations’ Eurographics 98 ICST.London
1998
25. Coates
Jackson& Broughton in : Ed P.Bentley “Evolutionary design by computers”
Chapter 14. Morgan Kaufmann 1999
26. Coates
& Makris “Genetic programming and spatial morphogenisis AISB 1999 Edinburgh
27. Coates & Schmidt “Parallel architecture” ECAADE 1999 Liverpool
28. Coates & Thum “Agent based modelling” Greenwich 2000 University of Greenwich London 2000